Đề thi thử Đại học năm 2013 – môn Toán (Đề 3)

ĐỀ THI THỬ ĐẠI HỌC – CAO ĐẲNG
NĂM 2012 – 2013

Bạn đang đọc: Đề thi thử Đại học năm 2013 – môn Toán (Đề 3)

MÔN THI: TOÁN

Đề số 03

PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)

Câu I (2 điểm)

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

2. Viết phương trình tiếp tuyến của (C), biết khoảng cách từ điểm I(1;2) đến tiếp tuyến bằng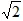

Câu II (2 điểm)

1) Giải phương trình: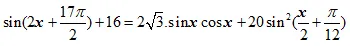

2) Giải hệ phương trình: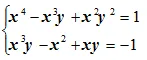

Câu III (1 điểm):

Tính tích phân:

Câu IV (1 điểm):

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB = a, các mặt bên là các tam giác cân tại đỉnh S. Hai mặt phẳng (SAB) và (SAC) cùng tạo với mặt phẳng đáy góc 60⁰. Tính côsin của góc giữa hai mặt phẳng (SAB) và (SBC) .

Câu V: (1 điểm) Cho a,b,c là các số dương thỏa mãn a + b + c = 1. Chứng minh rằng:

PHẦN RIÊNG (3 điểm) Thí sinh chỉ được làm một trong hai phần (phần A hoặc B)

A. Theo chương trình Chuẩn

Câu VI.a (1 điểm)

Trong mặt phẳng tọa độ Oxy cho điểm A(1;1) và đường thẳng d: 2x + 3y + 4 = 0.

Tìm tọa độ điểm B thuộc đường thẳng d sao cho đường thẳng AB và d hợp với nhau góc 45⁰.

Câu VII.a (1 điểm): Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;-1;1) và hai đường thẳng

Chứng minh: điểm M, (d), (d’) cùng nằm trên một mặt phẳng. Viết phương trình mặt phẳng đó.

Câu VIII.a (1 điểm)

Giải phương trình:

Theo chương trình Nâng cao

Câu VI.b (1 điểm)

Trong mặt phẳng tọa độ Oxy cho đường tròn (C): x² + y² = 1, đường thẳng (d): x + y + m = 0. Tìm m để (C) cắt (d) tại A và B sao cho diện tích tam giác ABO lớn nhất.

Câu VII.b (1 điểm)

Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng: (P): 2x – y + z + 1 = 0, (Q): x – y + 2z + 3 = 0, (R): x + 2y – 3z + 1 = 0 và đường thẳng . Gọi ∆₂ là giao tuyến của (P) và (Q).

Viết phương trình đường thẳng (d) vuông góc với (R) và cắt cả hai đường thẳng ∆₁, ∆₂

Câu VIII.b (1 điểm) Giải bất phương trình:

Download tài liệu để xem thêm chi tiết