|
SỞ GIÁO DỤC VÀ ĐÀO TẠO Bạn đang đọc: Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán – Bắc Giang ĐỀ THI CHÍNH THỨC |
ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2012-2013 Môn thi: Toán Thời gian: 120 phút không kể thời gian giao đề |
Câu 1. (2 điểm)
1.Tính: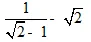 
2. Xác định giá trị của a,biết đồ thị hàm số y = ax – 1 đi qua điểm M(1;5)
Câu 2: (3 điểm)
1. Rút gọn biểu thức:
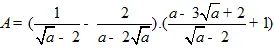với a>0,a
2. Giải hệ phương trình:
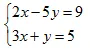
3. Chứng minh rằng pt: x2 + mx + m – 1 =0 luôn có nghiệm với mọi giá trị của m.
Giả sử x1,x2 là 2 nghiệm của pt đã cho, tìm giá trị nhỏ nhất của biểu thức: B = x12 + x22 – 4(x1 + x2)
Câu 3: (1,5 điểm)
Một ôtô tải đi từ A đến B với vận tốc 40km/h. Sau 2 giờ 30 phút thì một ôtô taxi cũng xuất phát đi từ A đến B với vận tốc 60 km/h và đến B cùng lúc với xe ôtô tải. Tính độ dài quãng đường AB.
Câu 4: (3 điểm)
Cho đường tròn (O) và một điểm A sao cho OA=3R. Qua A kẻ 2 tiếp tuyến AP và AQ của đường tròn (O), với P và Q là 2 tiếp điểm. Lấy M thuộc đường tròn (O) sao cho PM song song với AQ. Gọi N là giao điểm thứ 2 của đường thẳng AM và đường tròn (O). Tia PN cắt đường thẳng AQ tại K.
1.Chứng minh APOQ là tứ giác nội tiếp.
2.Chứng minh KA2=KN.KP
3.Kẻ đường kính QS của đường tròn (O).Chứng minh tia NS là tia phân giác của góc.
4. Gọi G là giao điểm của 2 đường thẳng AO và PK . Tính độ dài đoạn thẳng AG theo bán kính R.
Câu 5: (0,5điểm)
Cho a,b,c là 3 số thực khác không và thoả mãn:
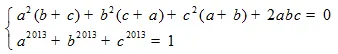
Hãy tính giá trị của biểu thức: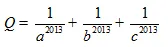 
Download tài liệu để xem thêm chi tiết
