Định lý Pitago được coi là một trong những tiền đề cơ bản trong hình học. Định lí Py-ta-go là nền tảng để các em giải những bài tập phức tạp sau này. Do đó, hãy tập trung chuyên sâu học và ghi nhớ công thức này nhé.
Bạn đang đọc: Định lý Pitago
Định lý Pitago còn được tổng quát hóa bằng nhiều cách khác nhau, bao gồm cho không gian đa chiều, không gian phi Euclid, cho các tam giác bất kỳ,… Định lý Pytago còn thu hút nhiều sự chú ý từ bên ngoài phạm vi toán học, như là một biểu tượng toán học thâm sâu, bí ẩn, hay sức mạnh của trí tuệ; nó còn được nhắc tới khá nhiều trong văn học, âm nhạc, con tem hay phim ảnh. Vậy sau đây là toàn bộ kiến thức về Định lý Pytago và các dạng bài tập kèm theo mời các bạn cùng theo dõi. Bên cạnh đó các bạn xem thêm cách chứng minh tam giác vuông.
Tổng hợp kiến thức về Định lí Py-ta-go
I. Nhà toán học Pytago (Pythagoras)
Trong toán học, định lý Pi – ta – go là một liên hệ giữa hình học phẳng giữa các cạnh trong một tam giác vuông
– Pythagoras (sinh khoảng 580 đến 572 TCN – mất khoảng năm 500 đến 490 TCN) là một nhà triết học người Hy Lạp và là người sáng lập ra phong trào tín ngưỡng có tên thuyết học Pythagoras. Ông thường được biết đến như một nhà khoa học và toán học vĩ đại. Trong tiếng việt, tên của ông thường được phiên âm từ tiếng Pháp (Pythagore) thành Py – ta – go
– Pythagoras đã thành công trong việc chứng minh tổng ba góc của một tam giác bằng 1800 và nổi tiếng nhất nhờ định lý toán học mang tên ông, Ông cũng được biết đến là “cha đẻ của số học”. Ông đã có nhiều đóng góp quan trọng cho triết học và tín ngưỡng vào cuối thế kỷ 7 TCN. Về cuộc đời và sự nghiệp của ông, có quá nhiều các huyền thoại khiến việc tìm lại sự thật lịch sử không dễ dàng. Pythagoras và các học trò của ông tin rằng mọi sự vật đều liên hệ đến Toán học và mọi sự việc đều có thể tiên đoán qua các chu kỳ.
II. Lý thuyết Định lí Py-ta-go
1. Định lý Pitago
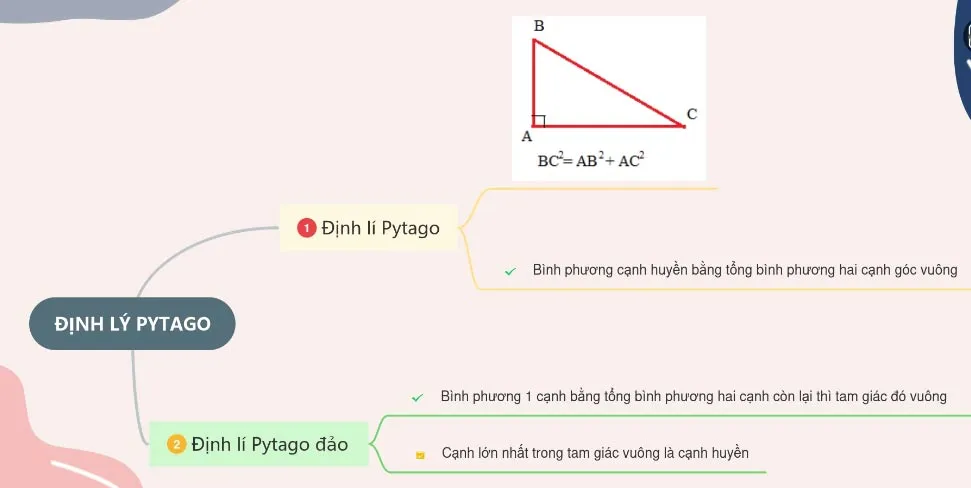
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
ΔABC vuông tại A ⇒ BC2 = AB2 + AC2
2. Công thức Pytago đảo
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
ΔABC có BC2 = AB2 + AC2 ∠BAC = 90o
3. Sơ đồ tư duy định lý Py-ta-go
III. Bài tập trắc nghiệm Định lí Py-ta-go
Bài 1: Cho tam giác ABC vuông tại B. Khi đó
A. AB2 + BC2 = AC2
B. AB2 – BC2 = AC2
C. AB2 + AC2 = BC2
D. AB2 = AC2 + BC2
Ta có tam giác ABC vuông tại B, theo định lí Py – ta – go ta có: AB2 + BC2 = AC2
Chọn đáp án A.
Bài 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2dm
A. BC = 4 dm
B. BC = √6 dm
C. BC = 8dm
D. BC = √8 dm
Áp dụng định lí Py – ta – go ta có: BC2 = AB2 + AC2
Khi đó ta có:
Chọn đáp án D.
Bài 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm
B. 10 cm, 24 cm
C. 12 cm, 24 cm
D. 15 cm, 24 cm
Gọi độ dài các cạnh góc vuông lần lượt là x, y (x, y > 0)
Theo định lí Py – ta – go ta có: x2 + y2 = 262 ⇔ x2 + y2 = 676
Theo bài ra ta có:
Khi đó ta có:
Chọn đáp án B.
Bài 4: Cho tam giác ABC vuông tại A có AC = 20cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16cm. Tính độ dài cạnh AB, AH ?
A. AH = 12cm, AB = 15cm
B. AH = 10cm, AB = 15cm
C. AH = 15cm, AB = 12cm
D. AH = 12cm, AB = 13cm
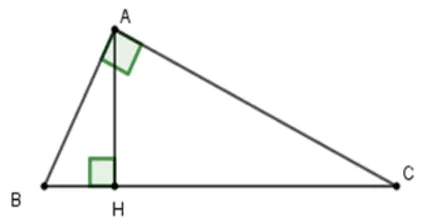
Ta có: BC = HB + HC = 9 + 16 = 25 (cm)
Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:
BC2 = AB2 + AC2 ⇒ AB2 = BC2 – AC2 = 252 – 202 = 225 ⇒ AB = 15cm
Xét tam giác ABH vuông tại H, theo định lí Py – ta – go ta có:
HB2 + HA2 = AB2 ⇒ AH2 = AB2 – HB2 = 152 – 92 = 144 ⇒ AH = 12cm
Vậy AH = 12cm, AB = 15cm
Chọn đáp án A.
Bài 5: Cho hình vẽ. Tính x
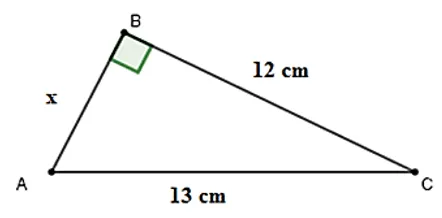
A. x = 10cm
B. x = 11cm
C. x = 8cm
D. x = 5cm
Xét tam giác ABC vuông tại B ta có:
⇒ x2 + 122 = 132 ⇒ x2 = 132 – 122 = 25
Khi đó: x = 5cm
Chọn đáp án D.
IV. Bài tập tự luận Định lí Py-ta-go
Câu 1
Tìm độ dài x trên hình 127.
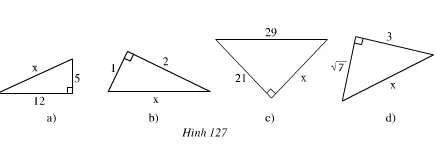
Giải
– Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
– Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
⇒ x = √5
Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 – 212 = 841 – 441 = 400
⇒ x = 20
– Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16
⇒ x = 4
Câu 2. Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.
Vẽ hình minh họa:
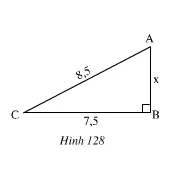
Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:
AB2 + BC2 = AC2
Nên AB2 = AC2 – BC2
= 8,52 – 7,52
= 72,25 – 56,25
=16
⇒ AB = 4 (m)
Giải
Vẽ hình minh họa:
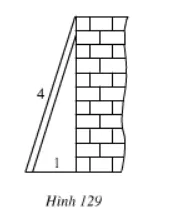
Kí hiệu như hình vẽ:
Vì mặt đất vuông góc với chân tường nên góc C = 90º.
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AC2 + BC2 = AB2
⇒ AC2 = AB2 – BC2 = 16 – 1 = 15
⇒ AC = √15 ≈ 3,87(m) hay chiều cao của bức tường là 3,87m.
Câu 4. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau.
a) 9cm, 15cm, 12cm.
b) 5dm, 13dm, 12dm.
c) 7m, 7m, 10m.
Giải
a) Ta có 92 = 81 ; 152 =225 ; 122 =144
Mà 225 = 144 + 81
Nên Theo định lí Py – ta – go đảo, tam giác có độ dài 3 cạnh 9cm ,12cm ,15cm là tam giác vuông.
b) Ta có 52 = 25 ; 132 =169 ; 122 =144
Mà 169 = 144 + 25
Nên Theo định lí Py – ta – go đảo tam giác có độ dài 3 cạnh 5dm ,13dm ,12dm là tam giác vuông.
c) Ta có 72 = 49 ; 102 =100
Mà 100 ≠ 49 + 49
Nên tam giác có độ dài 3 cạnh 7m, 7m, 10m không là tam giác vuông
V. Bài tập tự luyện định lý Pitago
Bài 1:
Cho DABC vuông tại A. biết AB + AC = 49cm; AB – AC = 7cm. Tính cạnh BC.
Bài 2:
Cho DABC vuông tại A. có BC = 26cm, AB:AC = 5:12. Tính độ dài AB và AC.
Bài 3:
Cho DABC vuông tại A. Kẻ đ ường cao AH. Biết BH = 18 cm; CH = 32cm. Tính các cạnh AB và AC.
Bài 4:
Cho DABC có AB = 9cm; AC = 11cm. Kẻ đường cao AH, bi ết BH = 26cm. Tính CH ?
Bài 5: Cho DABC vuông tại A. Kẻ AH vuông góc BC.
a/ Chứng minh: AB2 + CH2 = AC2 + BH2
b/ Trên AB lấy E, trên AC lấy đi ểm F. Ch ứng minh: EF
c/ Bi ết AB = 6cm, AC = 8 cm. Tính AH, BH, CH.
Bài 6:
Cho DABC cân, AB = AC = 17cm. Kẻ BD vuông góc AC. Tính BC, biết BD = 15cm.
Bài 7: Cho DABC. Biết BC = 52cm, AB = 20cm, AC = 48cm.
a/ CM: DABC vuông ở A.
b/ Kẻ AH vuông góc BC. Tính AH.
Bài 8:
Hãy kiểm tra xem tam giác ABC có phải là tam giác vuông không nếu các cạnh AB, AC và BC tỉ lệ với:
a/ 9; 12 và 15 b/ 3; 2,4 và 1,8.
c/ 4; 6 và 7 d/ 4; 4 và 4.
Bài 9: Cho DABC vuông tại A, đường cao AH, trên đó lấy điểm D. Trên tia đối của tia HA lấy E sao cho HE = AD. Đường vuông góc với AH tại D cắt AC tại F.
Chứng minh rằng: EB vuông góc EF.
Bài 10: Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).
a) Chứng minh tam giác HAB là tam giác cân
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Chứng minh BC ⊥ Ox.
c) Khi góc xOy bằng 600, chứng minh OA = 2OD.
Bài 11:
Cho tam giác ABC cân tại A. Gọi M, N là trung điểm các cạnh AB, AC. Các đường thẳng vuông góc với AB, AC tại M; N cắt nhau tại điểm O, AO cắt BC tại H. Chứng minh:
a. AMO = ANO
b. AH là phân giác của góc A
c. HB = HC và AH ⊥ BC
d. So sánh OC và HB
Bài 12: Cho tam giác cân ABC (AB = AC). Từ trung điểm M của BC vẽ ME ⊥ AC và MF ⊥AC. Chứng minh:
a. BEM = CFM
b. AE = AF
c. AM là phân giác của góc EMF
d. So sánh MC và ME
Bài 13: Cho tam giác ABC có = 900 , AB = 8cm, AC = 6cm .
a. Tính BC .
b. Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC .
c. Chứng minh DE đi qua trung điểm cạnh BC
Bài 14: Cho góc nhọn xOy, trên 2 cạnh Ox, Oy lần lượt lấy 2 điểm A và B sao cho OA = OB, tia phân giác của góc xOy cắt AB tại I.
a) Chứng minh OI ⊥ AB .
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OI Chứng minh BC ⊥ Ox .
Bài 15: Cho tam giác nhọn ABC có AB > AC, vẽ đường cao AH.
a. Chứng minh HB > HC
b. So sánh góc BAH và góc CAH.
c. Vẽ M, N sao cho AB, AC lần lượt là trung trực của các đoạn thẳng HM, HN. Chứng minh tam giác MAN là tam giác cân.

