Đường trung bình của hình thang

Đường trung bình của hình thang là gì? Cách tính đường trung bình của hình thang như thế nào? Mời quý thầy cô cùng các bạn học sinh lớp 8 theo dõi bài viết dưới đây.

Bạn đang đọc: Đường trung bình của hình thang

Đường trung bình của hình thang là tài liệu hữu ích được biên soạn đầy đủ lý thuyết và các dạng bài tập có đáp án kèm theo. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi học kì môn Toán. Vậy sau đây là nội dung chi tiết tài liệu cách tính đường trung bình của hình thang, mời các bạn cùng theo dõi tại đây.

Đường trung bình của hình thang

1. Hình thang là gì?

Hình thang là tứ giác có hai cạnh đối song song

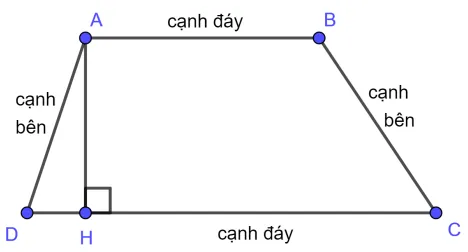
Hình thang ABCD (AB // CD):

AB và CD gọi là các cạnh đáy ( hoặc đáy). AB là đáy nhỏ, CD là đáy lớn.

AD và BC gọi là các cạnh bên.

Gọi AH là đường cao kẻ từ A đến CD. Khi đó, AH là đường cao của hình thang.

– Các trường hợp đặc biệt của hình thang:

– Hình thang vuông: là hình thang có một góc vuông.

– Hình thang cân: là hình thang có hai góc kề một cạnh đáy bằng nhau.

2. Đường trung bình của hình thang

a. Khái niệm

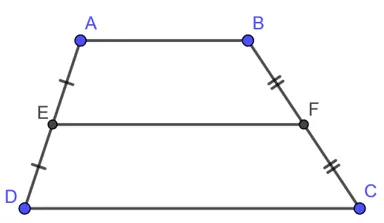
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang

b. Các định lí

– Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của cạnh bên thứ hai.

– Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

EF là đường trung bình của hình thang ABCD. Khi đó:

3. Bài tập về đường trung bình của hình thang

Bài 1: Một hình thang cân có cạnh bên là 2,5cm, đường trung bình là 3cm. Tính chu vi của
hình thang đó.

Giải:

Tổng hai cạnh đáy của hình thang là : 3 x 2 = 6 (cm)

Chu vi hình thang là : 6 + 2,5 + 2,5 = 11 (cm)

Đáp số : 11 cm

Bài 2

Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

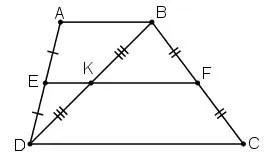
Giải:

Để chứng minh 3 điểm E, F, K thẳng hàng ta có thể chứng minh 2 trong 3 đoạn EK, FK, EF cùng // với AB và CD (theo tiên đề Ơcolit) thông qua tính chất đường trung bình của tam giác và hình thang.

‍Xét hình thang ABCD, có:

E là trung điểm của cạnh bên AD (gt)

F là trung điểm của cạnh bên BC (gt)

⇒ EF là đường trung bình của hình thang ABCD (theo định lí 3)

⇒ EF // AB // CD (theo định lí 4) (1)

Xét △ABD△ABD, có:

E là trung điểm của AD (gt)

K là trung điểm của BD (gt)

⇒ EK là đường trung bình của tam giác ABD (theo định lí 1)

⇒ EK // AB (theo định lí 2) (2)

Từ (1), (2) ⇒ E, F, K thẳng hàng (Theo tiên đề Ơcơlit).