Download.vn Học tập Lớp 8 Toán 8
Bạn đang đọc: Đường trung bình của tam giác, hình thang lớp 8
Đường trung bình của tam giác, hình thang lớp 8 Định nghĩa, định lý và bài tập áp dụng
Giới thiệu Tải về Bình luận
- 4
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Nhằm giúp các bạn học sinh có thêm nhiều tài liệu học tập, Download.vn giới thiệu Đường trung bình của tam giác, hình thang lớp 8.
Tài liệu bao gồm 37 trang tổng hợp toàn bộ kiến thức lý thuyết, định nghĩa, định lý phân dạng và hướng dẫn giải chi tiết các dạng toán cơ bản của tam giác và hình thang. Qua tài liệu này các bạn có thêm nhiều tư liệu tham khảo củng cố kiến thức chương 1: Tứ giác. Nội dung chi Ngoài ra bạn đọc tham khảo thêm tài liệu bài tập tổng hợp về Hằng đẳng thức. Chúc các bạn học tập tốt.
Đường trung bình của tam giác, hình thang lớp 8
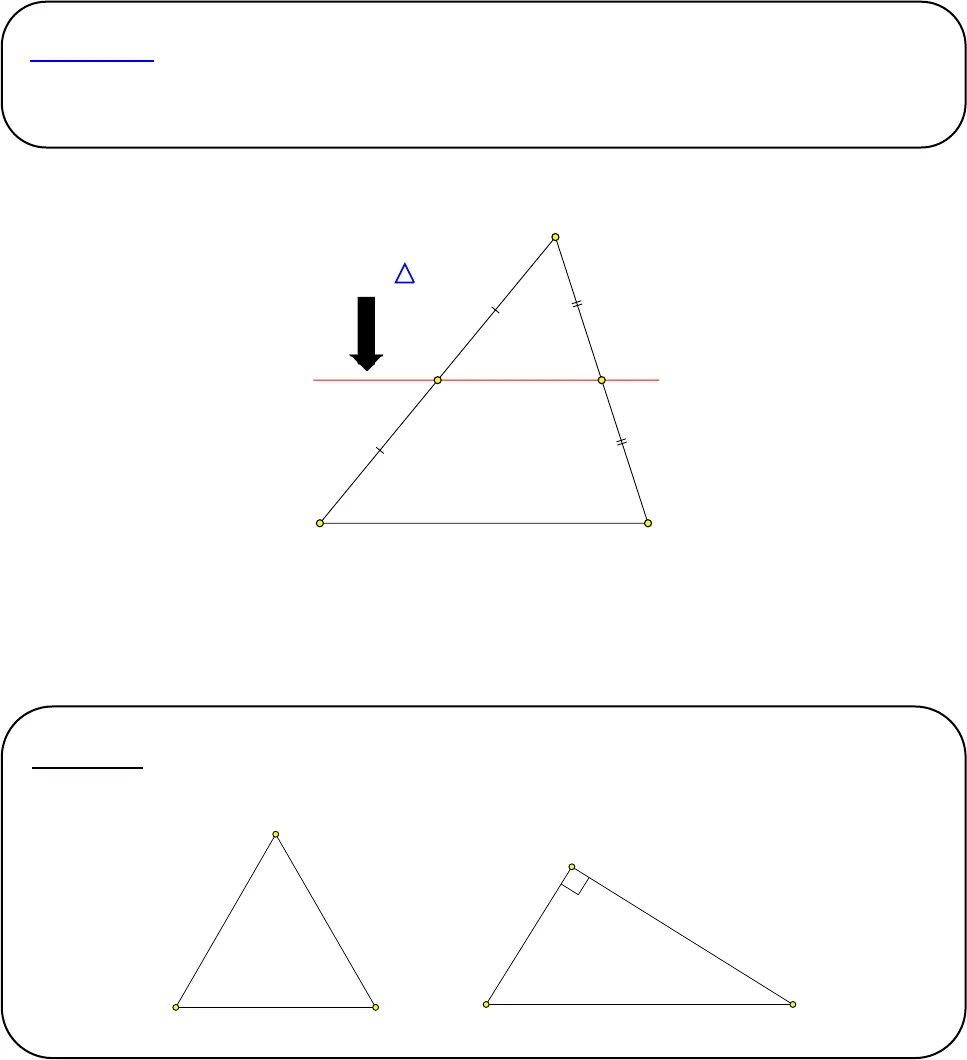GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro1CHƯƠNG V – TỨ GIÁC CHỦ ĐỀ 3 – ĐƯỜNG TRUNG BÌNH. A. LÝ THUYẾT 1. Đường trung bình của tam giác: 1.1. Định nghĩa Đường thẳng là đường trung bình của tam giác ABC vì đi qua trung điểm M, N của hai cạnh bên. Đường trungbình củaABCABCMNaĐịnh nghĩa: Đường trung bình của tam giác là đường thẳng đi qua trung điểm của hai cạnh tam giác Ví dụ 1: Hãy vẽ đường trung bình của các tam giác sau. PNMGFE
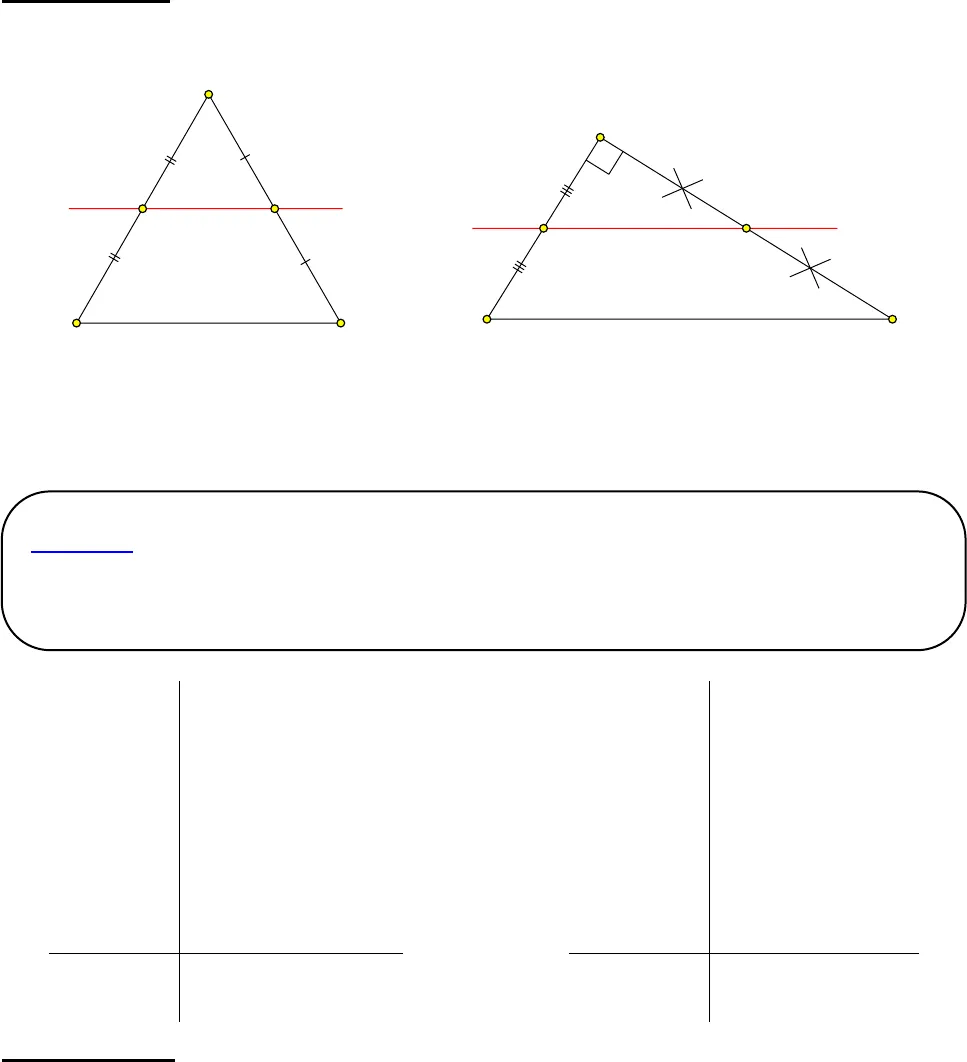GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro2Hướng dẫn giải: 2. Định lý:Giả thiết ABC M AB, MA = MB M d // BC d cắt AC tại NHoặc Giả thiết ABC M trung điểm AB M d // BC d cắt AC tại NKết luậnN AC, NA = NC Kết luậnN trung điểm ACCHỨNG MINH: Dựng đường thẳng qua N song song với AB, cắt BC tại P(so le trong) (1) (so le trong) (2)MN // BC (so le trong) (3)Từ (1)(3) suy ra Hình thang MNPB có MB // NP MB = NP EFGMNPabIJKLĐịnh lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba. 
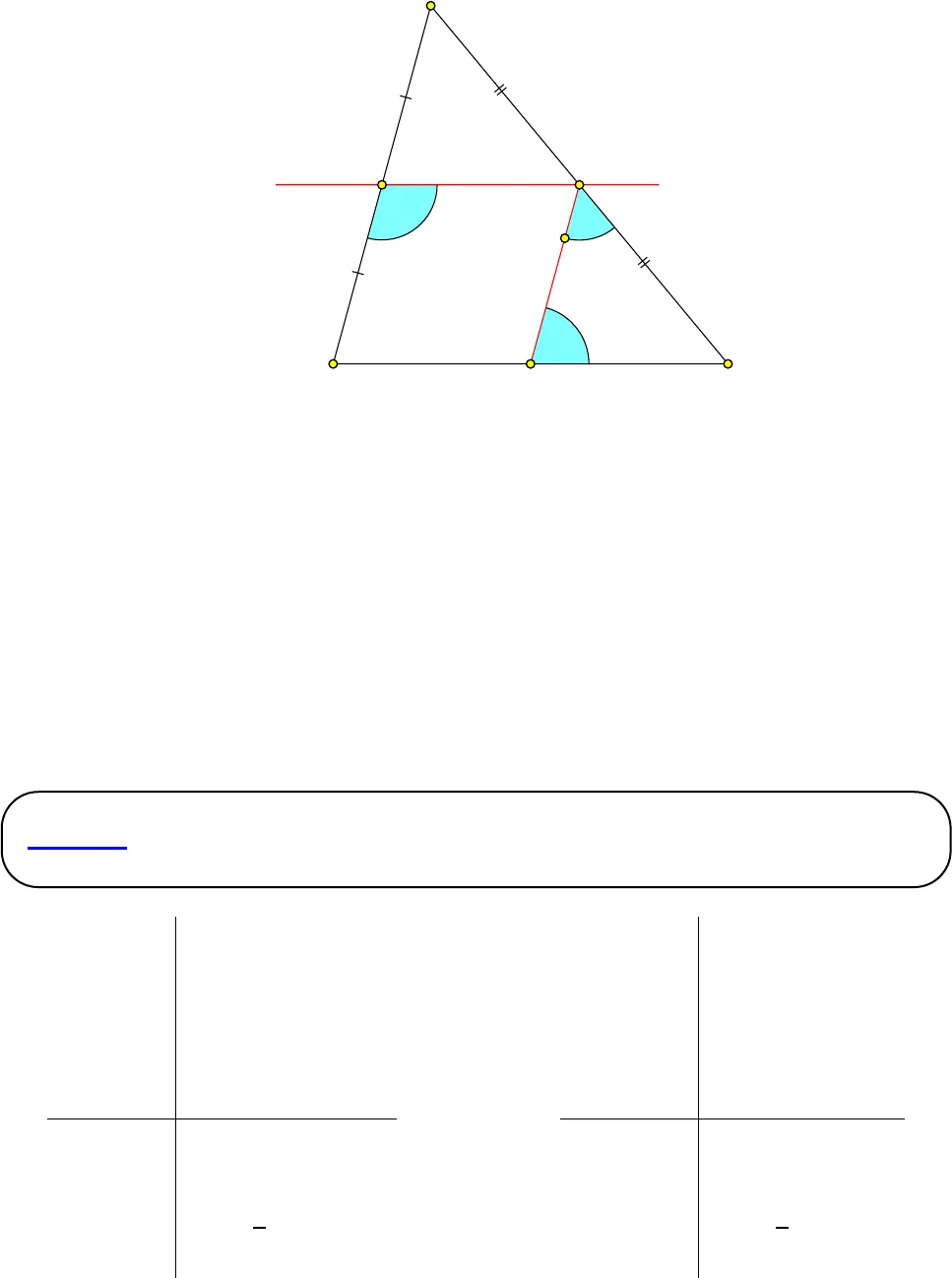GV: Thạc sĩ Bùi Đức Phương – SĐT 0906 434 811 Facebook: https://www.facebook.com/feo.pro3Mặt khác M trung điểm AB MB = MASuy ra MA = NPXét AMN & NPC có: ; ; MA = NPSuy ra AMN = NPC (g.c.g) NA = NC N là trung điểm AC.Giả thiết ABC M AB, MA = MB N AC, NA = NC Hoặc Giả thiết ABC M trung điểm AB N trung điểm AC Kết luậnMN // BC Kết luậnMN // BC dNMCBA111Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa cạnh ấy. 