Download.vn Học tập Lớp 12

Bạn đang đọc: Giải bài toán cực trị số phức bằng phương pháp hình học giải tích

Giải bài toán cực trị số phức bằng phương pháp hình học giải tích Giải số phức bằng hình học giải tích

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Giải bài toán cực trị số phức bằng phương pháp hình học giải tích là tài liệu hướng dẫn giải bài toán cực trị số phức bằng phương pháp hình học giải tích. Đây là lớp các bài toán vận dụng cao số phức và thường xuất hiện trong đề thi THPT Quốc gia.

Hy vọng với tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt kết quả cao trong các bài kiểm tra, bài thi học kì và thi THPT Quốc gia đạt kết quả cao. Đồng thời đây cũng là tài liệu hữu ích giúp quý thầy cô có thêm nhiều tư liệu trong giảng dạy. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Hướng dẫn giải bài tập số phức bằng hình học giải tích

Trang 1MỞ ĐẦUTrong chương trình Toán THPT, phần Đại số mà cụ thể là phần Số học, ở chươngtrình lớp 12, học sinh được hoàn thiện hiểu biết của mình về các tập hợp số thông quaviệc cung cấp một tập hợp số, gọi là Số phức. Trong chương này, học sinh đã bước đầulàm quen với các phép toán cộng, trừ, nhân, chia, khai căn, lũy thừa; lấy mô đun, …cácsố phức. Bằng cách đặt tương ứng mỗi số phức2,( ; , 1)z x yi x y i     với mỗiđiểm( ; )M x ytrên mặt phẳng tọa độOxy, ta thấy giữa Đại số và Hình học có mối liênhệ với nhau khá “gần gũi”. Hơn nữa, nhiều bài toán Đại số bên Số phức, khi chuyểnsang Hình học, từ những con số khá trừu tượng, bài toán đã được minh họa một cách rấttrực quan, sinh động và cũng giải được bằng Hình học với phương pháp rất đẹp. Đặcbiệt, trong các kỳ thi Đại học, Cao đẳng và THPT Quốc gia những năm gần đây, việc sửdụng phương pháp Hình học để giải quyết các bài toán về Số phức là một trong nhữngphương pháp khá hay và hiệu quả, đặc biệt là các bài toán về Cực trị trong số phức. Hơnnữa, với những bài toán Hình học theo phương pháp trắc nghiệm, nếu khi biểu diễnđược trên giấy thì qua hình ảnh minh họa, ta có thể lựa chọn đáp án một cách dễ dàng.Tuy nhiên, trong thực tế giảng dạy, việc chuyển từ bài toán Đại số nói chung vàSố phức nói riêng sang bài toán Hình học ở nhiều học sinh nói chung còn khá nhiềulúng túng, vì vậy việc giải các bài toán về Số phức gây ra khá nhiều khó khăn cho họcsinh.Bài toán Cực trị Số phức thông thường thì có khá nhiều cách lựa chọn để giải nhưdùng Bất đẳng thức, dùng Khảo sát hàm số, … Qua chuyên đề này, tôi muốn gợi ý chohọc sinh một lối tư duy vận dụng linh hoạt các phương pháp chuyển đổi từ bài toán Đạisố sang Hình học cho học sinh, giúp các em có cái nhìn cụ thể hơn về việc chuyển đổiđó và vận duy tư duy này cho những bài toán khác. Với mục tiêu đó, trong chuyên đềnày, tôi chỉ tập trung giải quyết bài toán theo hướng Hình học. Không đặt nặng việc sosánh phương pháp nào nhanh hơn, tối ưu hơn phương pháp nào. Trang 2II. NỘI DUNG1. Một số kiến thức, kí hiệu ban đầu1.1 Các định nghĩa và kí hiệua) Số i: Ta thừa nhận có một số mà bình phương của nó bằng1.Kí hiệu:.iNhư vậy,21.i  b) Số phức: Cho, ,x ybiểu thứcz x yi gọi là một (dạng đại số) số phức.:xPhần thực;:yPhần ảo c) Với mỗi số phức,z x yi giá trị biểu thức2 2x ygọi là mô đun của.zKíhiệu:z. Như vậy,2 2.z x y d) Với mỗi số phức.z x yi Số phức’ ( )z x y i x yi    gọi là số phức liênhợp của số phức.zKí hiệuz. Như vậy,z x yi thì.z x yi e) Với mỗi số phức.z x yi Xác định điểm( ; )M x ytrên mặt phẳng tọa độOxy. ĐiểmMgọi là biểu diễn hình học của số phức.zĐể cho tiện, trong tập tài liệu này, tôi kí hiệu( ; ) ( )M x y M z hay đơn giản( )M zđể chỉMlà điểm biểu diễn cho số phức.z x yi 1.2 Các phép toán trên tập hợp số phứcCho hai số phức2, ‘ ‘ ‘ .( , , ‘, ‘ , 1)z x yi z x y i x y x y i      + Phép cộng:’ ( ‘) ( ‘)z z x x y y i    + Phép trừ:’ ( ‘) ( ‘)z z x x y y i    + Phép nhân:. ‘ ( ‘ ‘) ( ‘ ‘ )z z xx yy xy x y i   + Phép chia:. ”’. ‘z z zzz zvới’ 0 0 .z i 1.3 Một số kí hiệu chuyển từ số phức sang tọa độ Oxy quen thuộc. + Với( )M zthì.z OM + Với( ), ‘ ‘( ‘)M M z M M z thì’ ‘.z z MM  + Với( ), ( ),A BA A z B B z  trong đó,A Bz zlà hai số phức khác nhau cho trướcthì tập hợp các điểm( )M M zthỏa mãn hệ thứcA Bz z z z   là đường trung trựccủa đoạn.AB + Với0 0 0( ),R 0M M z , tập hợp các điểm( )M M z thỏa mãn hệ thức0Rz z là đường tròn tâm0,Mbán kính R. 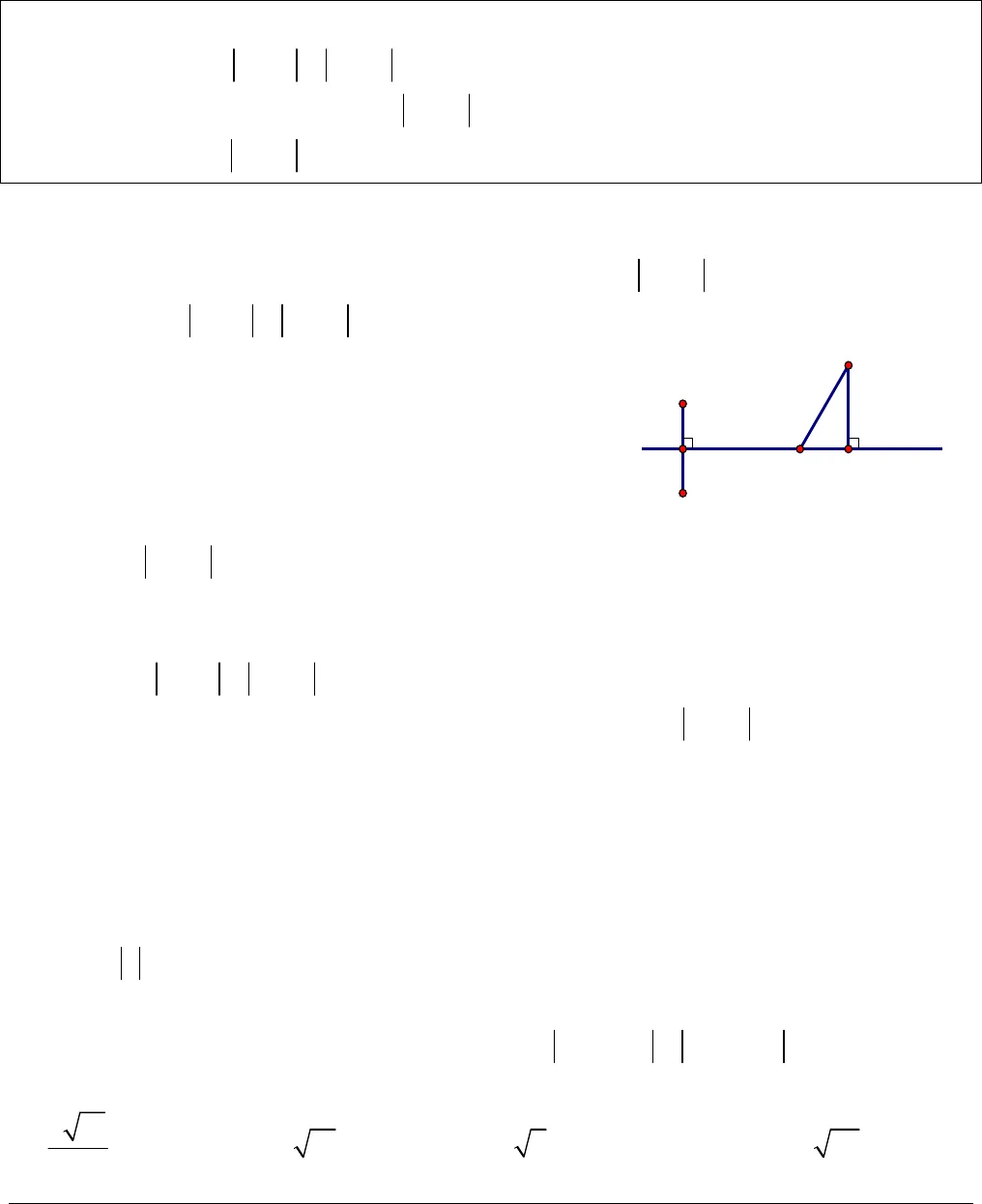Trang 32. Các bài toánBÀI TOÁN 1: Cho số phức0 0 0, ,z a b i a b  và tập hợp các số phứcz x yi thỏa mãn hệ thức:1 2.z z z z  a) Tìm giá trị nhỏ nhất của0z z b) Tìmzđể0z znhỏ nhấtNhận xét:+ Gọi( )M M z,0 0 0 1 2( ); ( ); ( )M M z A A z B B z  thì0 0z z MM + Từ đẳng thức1 2.z z z z  Suy ra,Mthuộc trung trựccủa đoạn AB.Bài toán chuyển thành:a) Tìm giá trị nhỏ nhất của0M Mvới.M b) TìmM sao cho0M Mnhỏ nhất+ Ta thấy, với mọi điểmM thì0 0,M M M Htrong đó H là hình chiếu của M0lên.Do đó,0 0min ( ; ).z z d M  Và để0M Mnhỏ nhất vớiM thìM Hhay M làhình chiếu của M0lên.Lời giải- Từ hệ thức1 2z z z z  , suy ra phương trình đường thẳng.+ Với câu a), ta tính khoảng cách0( ; ).d MVà kết luận,0 0min ( ; ).z z d M  + Với câu b),- Viết phương trình đường thẳng d đi qua M0, vuông góc với(hoặc song song với).AB– Giải hệ gồm hai phương trình:và d suy ra nghiệm( ; ).x yKết luận, số phức cần tìmlà.z x yi Đặc biệt:minztức là tìm số phứczsao cho mô đun củazlà nhỏ nhất.Ví dụ 1.1. Trong tất cả các số phức zthỏa mãn1 2 3 4 .z i z i    Tìm giá trị nhỏnhất của mô đun của.zA.5 1313B.2 13 C.2 D.26ΔA(z1)B(z2)M0HM