Giải Toán lớp 9 trang 10, 11, 12 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và 11 bài tập trong SGK bài 2 Căn thức bậc hai và hằng đẳng thức.
Bạn đang đọc: Giải Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức
Giải Toán 9 Bài 2 tập 1 Căn thức bậc hai và hằng đẳng thức được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 10, 11, 12 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Giải Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức
I. Trả lời câu hỏi trang 8 SGK Toán 9 tập 1
Câu 1
Hình chữ nhật ABCD có đường chéo AC = 5cm và cạnh BC = x (cm) thì cạnh . Vì sao? (h.2)
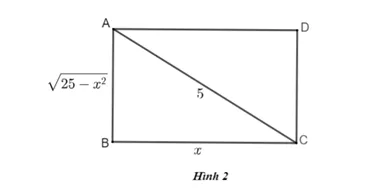
Hướng dẫn giải:
Áp dụng định lí Pi – ta – go vào tam giác ABC vuông tại B có:
0} right) cr}” width=”318″ height=”96″ data-type=”0″ data-latex=”eqalign{& A{B^2} + B{C^2} = A{C^2} Leftrightarrow A{B^2} + {x^2} = {5^2} cr & Leftrightarrow A{B^2} = 25 – {x^2} cr & Rightarrow AB = sqrt {left( {25 – {x^2}} right)} ,,,left( {do,,AB > 0} right) cr}” data-i=”2″ data-src=”https://tex.vdoc.vn/?tex=%5Ceqalign%7B%26%20A%7BB%5E2%7D%20%2B%20B%7BC%5E2%7D%20%3D%20A%7BC%5E2%7D%20%5CLeftrightarrow%20A%7BB%5E2%7D%20%2B%20%7Bx%5E2%7D%20%3D%20%7B5%5E2%7D%C2%A0%20%5Ccr%20%26%C2%A0%20%5CLeftrightarrow%20A%7BB%5E2%7D%20%3D%2025%20-%20%7Bx%5E2%7D%C2%A0%20%5Ccr%20%26%C2%A0%20%5CRightarrow%20AB%20%3D%20%5Csqrt%20%7B%5Cleft(%20%7B25%20-%20%7Bx%5E2%7D%7D%20%5Cright)%7D%20%5C%2C%5C%2C%5C%2C%5Cleft(%20%7Bdo%5C%2C%5C%2CAB%20%3E%200%7D%20%5Cright)%20%5Ccr%7D”>
Câu 2
Với giá trị nào của x thì xác định?
Hướng dẫn giải:
Điều kiện để căn thức xác định (có nghĩa) là:
Câu 3
Điền số thích hợp vào ô trống trong bảng sau:
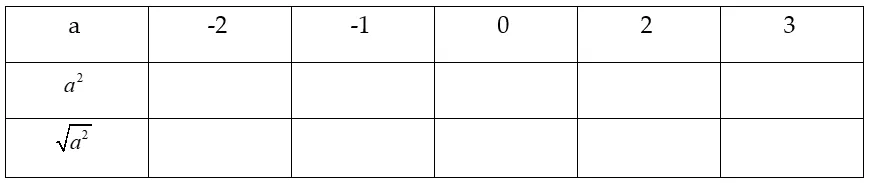
Hướng dẫn giải:
|
a |
-2 |
-1 |
0 |
2 |
3 |
|
a2 |
4 |
1 |
0 |
4 |
9 |
| √ a 2 |
2 |
1 |
0 |
2 |
3 |
II. Giải bài tập toán 9 trang 10, 11, 12 tập 1
Bài 6 (trang 10 SGK Toán 9 Tập 1)
Với giá trị nào của a thì mỗi căn thức sau có nghĩa:
Gợi ý đáp án
a) Ta có: có nghĩa khi
b) Ta có: có nghĩa khi
c) Ta có: có nghĩa khi
d) Ta có: có nghĩa khi
Bài 7 (trang 10 SGK Toán 9 Tập 1)
Tính:
c.
d.
Gợi ý đáp án
a)
Ta có:
b)
Ta có:
c)
Ta có:
d)
d.
Ta có:
= – 0,16
Bài 8 (trang 10 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a)
c) với a ≥ 0
b)
d) với a
Gợi ý đáp án
a)
Ta có:
(Vì 4>3 nên sqrt{3} Leftrightarrow 2> sqrt{3} Leftrightarrow 2- sqrt{3}>0 .” width=”287″ height=”23″ data-latex=”sqrt{4} > sqrt{3} Leftrightarrow 2> sqrt{3} Leftrightarrow 2- sqrt{3}>0 .” data-src=”https://tex.vdoc.vn?tex=%5Csqrt%7B4%7D%20%3E%20%5Csqrt%7B3%7D%20%5CLeftrightarrow%202%3E%20%5Csqrt%7B3%7D%20%5CLeftrightarrow%202-%20%5Csqrt%7B3%7D%3E0%20.”>
b)
Ta có:
(Vì 9
c) với a ≥ 0
Ta có:
d) với a
Vì a
Do đó:
Bài 9 (trang 11 SGK Toán 9 Tập 1)
Tìm x biết:
a)
b)
c)
d)
Gợi ý đáp án
a)
Ta có:
Vậy
b)
Ta có:
Vậy
c)
Ta có:
Vậy
d)
Ta có:
Vậy
Bài 10 (trang 11 SGK Toán 9 Tập 1)
Chứng minh
a)
b)
Gợi ý đáp án
a)
Ta có:
Vậy
b)
Ta có:
(do 1 Leftrightarrow sqrt 3 > sqrt 1 Leftrightarrow sqrt 3 > 1 Leftrightarrow sqrt 3 -1 > 0″ width=”354″ height=”24″ data-latex=”3>1 Leftrightarrow sqrt 3 > sqrt 1 Leftrightarrow sqrt 3 > 1 Leftrightarrow sqrt 3 -1 > 0″ data-src=”https://tex.vdoc.vn?tex=3%3E1%20%5CLeftrightarrow%20%5Csqrt%203%20%3E%20%5Csqrt%201%20%5CLeftrightarrow%20%5Csqrt%203%20%3E%201%20%5CLeftrightarrow%20%5Csqrt%203%20-1%20%3E%200″>
III. Giải bài tập toán 9 trang 11, 12 tập 1: Luyện tập
Bài 11 (trang 11 SGK Toán 9 Tập 1)
Tính:
a)
b)
c)
d)
Gợi ý đáp án
a) Ta có:
=4.5+14:7
=20+2=22 .
b) Ta có:
=36:18-13
=2-13=-11.
c) Ta có:
d) Ta có:
Bài 12 (trang 11 SGK Toán 9 Tập 1)
Tìm x để mỗi căn thức sau có nghĩa:
a)
c)
c.
d)
Gợi ý đáp án
a) Ta có:
có nghĩa khi và chỉ khi:
b) Ta có
có nghĩa khi và chỉ khi:
c) Ta có:
có nghĩa khi và chỉ khi:
0″ width=”218″ height=”42″ data-latex=”displaystyle {1 over displaystyle { – 1 + x}} ge 0 Leftrightarrow – 1 + x > 0″ data-src=”https://tex.vdoc.vn?tex=%5Cdisplaystyle%20%7B1%20%5Cover%20%5Cdisplaystyle%20%7B%20-%201%20%2B%20x%7D%7D%20%5Cge%200%20%5CLeftrightarrow%20-%201%20%2B%20x%20%3E%200″>
1″ width=”68″ height=”16″ data-latex=”Leftrightarrow x > 1″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%20x%20%3E%201″>
d)
Ta có:, với mọi số thực x
, (Cộng cả 2 vế của bất đẳng thức trên với 1)
, mà 1 >0
0″ width=”109″ height=”21″ data-latex=”Leftrightarrow x^2+1 >0″ data-src=”https://tex.vdoc.vn?tex=%5CLeftrightarrow%20x%5E2%2B1%20%3E0″>
Vậy căn thức trên luôn có nghĩa với mọi số thực x.
Bài 13 (trang 11 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) với a
b) với a ≥ 0.
c)
d) với a
Gợi ý đáp án
a) Ta có:
=-2a-5a
=(-2-5)a
=-7a
Vậy
b) Ta có:
=5a+3a
=(5+3)a
=8a.
(vì )
c) Ta có:
(Vì với mọi
).
d) Ta có:
(vì a)
=
Bài 14 (trang 11 SGK Toán 9 Tập 1)
Phân tích thành nhân tử:
a) x2 – 3 ;
b) x2 – 6
c) x2 + 2√3 x + 3 ;
d) x2 – 2√5 x + 5
Gợi ý đáp án
a) x2 – 3 = x2 – (√3)2 = (x – √3)(x + √3)
b) x2 – 6 = x2 – (√6)2 = (x – √6)(x + √6)
c) x2 + 2√3 x + 3 = x2 + 2√3 x + (√3)2
= (x + √3)2
d) x2 – 2√5 x + 5 = x2 – 2√5 x + (√5)2
=
Bài 15 (trang 11 SGK Toán 9 Tập 1)
Giải các phương trình sau:
a) x2 – 5 = 0 ;
b) x2 – 2√11 x + 11 = 0
Gợi ý đáp án
a) x2 – 5 = 0 ⇔ x2 = 5 ⇔ x1 = √5; x2 = -√5
Vậy phương trình có hai nghiệm x1 = √5; x2 = -√5
Cách khác:
x2 – 5 = 0 ⇔ x2 – (√5)2 = 0
⇔ (x – √5)(x + √5) = 0
hoặc x – √5 = 0 ⇔ x = √5
hoặc x + √5 = 0 ⇔ x = -√5
b) x2 – 2√11 x + 11 = 0
⇔ x2 – 2√11 x + (√11)2 = 0
⇔ (x – √11)2 = 0
⇔ x – √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11
Bài 16 (trang 12 SGK Toán 9 Tập 1)
Đố. Hãy tìm chỗ sai trong phép chứng minh “Con muỗi nặng bằng con voi” dưới đây:
Giả sử con muỗi nặng m (gam), còn con voi nặng V (gam). Ta có:
m2 + V2 = V2 + m2
Cộng cả hai vế với -2Mv, ta có:
m2 – 2mV + V2 = V2 – 2mV + m2
hay (m – V)2 = (V – m)2.
Lấy căn bậc hai mỗi vế của đẳng thức trên, ta được:
√(m – V)2 = √(V – m)2
Do đó m – V = V – m
Từ đó ta có 2m = 2V, suy ra m = V. Vậy con muỗi nặng bằng con voi (!).
Gợi ý đáp án
Sai lầm ở chỗ: sau khi lấy căn hai vế của (m – V)2 = (V – m)2 ta phải được kết quả |m – V| = |V – m| chứ không thể có m – V = V – m (theo hằng đẳng thức √A2 = |A|.
Do đó, con muỗi không thể nặng bằng con voi.
IV. Lý thuyết Căn thức bậc hai và hằng đẳng thức ![Giải Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức]( "Giải Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức")
1. Căn thức bậc hai
Với là một biểu thức đại số, người ta gọi là căn thức bậc hai của A. Khi đó, A được gọi là biểu thức lấy căn hay biểu thức dưới dấu căn.
xác định hay có nghĩa khi A lấy giá trị không âm.
2. Hằng đẳng thức
Với mọi số a, ta có
* Một cách tổng quát, với A là một biểu thức ta có
nghĩa là
nếu
và
nếu A
3. Các dạng toán cơ bản
Dạng 1: Tìm điều kiện để căn thức xác định
Ta có xác định hay có nghĩa khi
Ví dụ: xác định khi
Dạng 2: Rút gọn biểu thức
Sử dụng: Với A là một biểu thức ta có
Vì dụ: Với x>2 ta có:
