Giải Toán lớp 9 trang 104 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 2 Đường kính và dây của đường tròn thuộc chương 2.
Bạn đang đọc: Giải Toán 9 Bài 2: Đường kính và dây của đường tròn
Giải Toán 9 Bài 2 Chương 2 Hình học được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 104 tập 1 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 9 Bài 2: Đường kính và dây của đường tròn
Trả lời câu hỏi Toán 9 Bài 2
Câu hỏi 1
Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Gợi ý đáp án
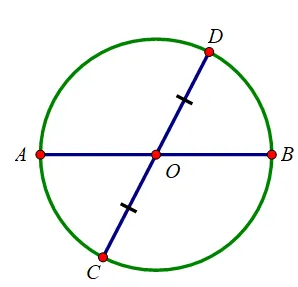
O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD
Câu hỏi 2
Cho hình 67. Hãy tính độ dài dây AB, biết OA = 13 cm, AM = MB, OM = 5 cm.
Gợi ý đáp án
Ta có:
OM là 1 phần đường kính đi qua trung điểm của AB
⇒ OM ⊥ AB
Xét tam giác OAM vuông tại M có:
 AB = 2AM = 24left( {cm} right) hfill
AB = 2AM = 24left( {cm} right) hfill
end{matrix}” width=”360″ height=”81″ data-type=”0″ data-latex=”begin{matrix}
O{A^2} = A{M^2} + O{M^2} hfill
Rightarrow AM = sqrt {O{A^2} – O{M^2}} = sqrt {{{13}^2} – {5^2}} = 12 hfill
= > AB = 2AM = 24left( {cm} right) hfill
end{matrix}” data-src=”https://tex.vdoc.vn/?tex=%5Cbegin%7Bmatrix%7D%0A%20%20O%7BA%5E2%7D%20%3D%20A%7BM%5E2%7D%20%2B%20O%7BM%5E2%7D%20%5Chfill%20%5C%5C%0A%20%20%20%5CRightarrow%20AM%20%3D%20%5Csqrt%20%7BO%7BA%5E2%7D%20-%20O%7BM%5E2%7D%7D%20%20%3D%20%5Csqrt%20%7B%7B%7B13%7D%5E2%7D%20-%20%7B5%5E2%7D%7D%20%20%3D%2012%20%5Chfill%20%5C%5C%0A%20%20%20%3D%20%20%3E%20AB%20%3D%202AM%20%3D%2024%5Cleft(%20%7Bcm%7D%20%5Cright)%20%5Chfill%20%5C%5C%20%0A%5Cend%7Bmatrix%7D”>
Giải bài tập toán 9 trang 104 tập 1
Bài 10
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE
Gợi ý đáp án
a) Gọi O là trung điểm của BC (1)
Vì DO là đường trung tuyến của tam giác vuông DBC.
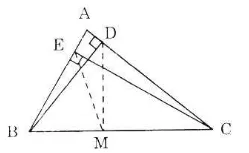
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
Từ (1) và (2) suy ra OD=OB=OC
Do đó ba điểm B,D, C cùng thuộc đường tròn tâm O bán kính OB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên
Suy ra ba điểm B, E, C cùng thuộc đường tròn tâm O bán kính OB.
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường với BC là đường kính.
Ta có DE là một dây cung không đi qua tâm nên ta có BC > DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
Bài 11
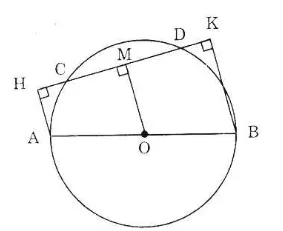
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Gợi ý đáp án
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
Lý thuyết Đường kính và dây của đường tròn
1. So sánh độ dài của đường kính và dây.
Định lý:
Trong các dây của một đường tròn, dây lớn nhất là đường kính.
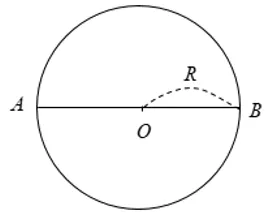
Xét đường tròn
2. Quan hệ vuông góc giữa đường kính và dây.
Định lý 1:
– Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung
CD AB tại H
=> H là trung điểm của AB
Định lý 2: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung, OAB
H là trung điểm của AB,
=> CD AB tại H

