Giải Toán lớp 9 trang 48 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 2 Hàm số bậc nhất thuộc chương 2 Hàm số bậc nhất.
Bạn đang đọc: Giải Toán 9 Bài 2: Hàm số bậc nhất
Giải Toán 9 Bài 2 tập 1 Hàm số bậc nhất được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 48 tập 1 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 9 Bài 2: Hàm số bậc nhất
Trả lời câu hỏi Toán 9 Bài 2
Câu hỏi 1
|
Hãy điền vào chỗ trống (…) cho đúng Sau 1 giờ, ô tô đi được: … Sau t giờ, ô tô đi được: … Sau t giờ, ô tô cách trung tâm Hà Nội là: s = … |
Gợi ý đáp án
Sau 1 giờ, ô tô đi được: 50 (km)
Sau t giờ, ô tô đi được: 50.t (km)
Sau t giờ, ô tô cách trung tâm Hà Nội là: s = 50.t – 8 (km)
Câu hỏi 2
Tính các giá trị tương ứng của s khi cho t lần lượt lấy các giá trị 1 giờ; 2 giờ; 3 giờ; 4 giờ; … rồi giải thích tại sao s là hàm số của t?
Gợi ý đáp án
Với t = 1, ta có s = 50.t – 8 = 50.1-8 = 42 (km)
Với t = 2, ta có s = 50.t – 8 = 50.2-8 = 92 (km)
Với t = 3, ta có s = 50.t – 8 = 50.3-8 = 142 (km)
Với t = 4, ta có s = 50.t – 8 = 50.4-8 = 92 (km)
Câu hỏi 3
Cho hàm số bậc nhất y = f(x) = 3x + 1.
Cho x hai giá trị bất kì x1, x2, sao cho x12. Hãy chứng minh f(x1) 2) rồi rút ra kết luận hàm số đồng biến trên R.
Gợi ý đáp án
Do x12 nên x1 – x2
Ta có: f(x1) – f(x2) = (3x1 + 1) – (3x2 + 1) = 3(x1 – x2 )
⇔ f(x1) 2)
Vậy hàm số y = 3x + 1 đồng biến trên R
Câu hỏi 4
Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:
a) Hàm số đồng biến;
b) Hàm số nghịch biến.
Gợi ý đáp án
a) Hàm số đồng biến là y = 8x + 1
b) Hàm số nghịch biến là y = -1,5x – 5
Giải bài tập Toán 9 trang 48 tập 1
Bài 8
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?
a) y = 1 – 5x ;
b) y = -0,5x
c) y = √2(x – 1) + √3 ;
d) y = 2×2 + 3
Gợi ý đáp án
a) y = 1 – 5x là hàm số bậc nhất có a = -5, b = 1, nghịch biến vì a = -5
b) y = -0,5x là hàm số bậc nhất có a = -0,5, b = 0, nghịch biến vì a = -0,5
c) y = √2(x – 1) + √3 = √2 x + √3 – √2 là hàm số bậc nhất có a = √2, b = √3 – √2, đồng biến vì a = √2 > 0
d) y = 2×2 + 3 không phải là hàm số bậc nhất (vì số mũ của x là 2)
Bài 9
Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số:
a) Đồng biến
b) Nghịch biến
Gợi ý đáp án
Hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a
a) y = (m – 2)x + 3 đồng biến khi m – 2 > 0 ⇔ m > 2
Vậy với m > 2 thì hàm số đồng biến.
b) y = (m – 2)x + 3 nghịch biến khi m – 2
Vậy với m
Bài 10
Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của nó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.
Gợi ý đáp án
Theo bài ra ta vẽ hình sau:
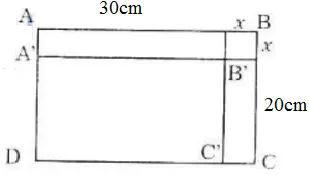
– Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
– Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A’B’C’D’ có:
A’B’ = 30 – x
B’C’ = 20 – x
Gọi y là chu vi của hình chữ nhật A’B’C’D’, ta có:
y = 2[(30 – x) + (20 – x)]
=> y = 2(50 – 2x)
=> y = -4x + 100 (cm)
Giải bài tập toán 9 trang 48 tập 1: Luyện tập
Bài 11
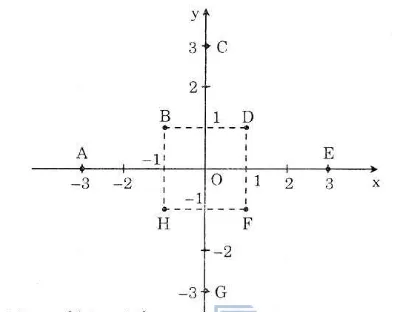
Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), F(1; -1), G(0; 3), H(-1; -1).
Gợi ý đáp án
Biểu diễn các điểm trên mặt phẳng tọa độ: A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), F(1; -1), G(0; 3), H(-1; -1). như hình vẽ sau:
Bài 12
Cho hai hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5.
Gợi ý đáp án
Thay x = 1, y = 2,5 vào y = ax + 3 ta được:
2,5 = a.1 + 3
=> a = 2,5 – 3 = -0,5
Vậy a = -0,5
Bài 13
Với những giá trị nào của m thì mỗi hàm số sau là hàm số bậc nhất ?
Gợi ý đáp án
a) Ta có
Hệ số là
Điều kiện để là hàm số hàm bậc nhất là:
 0 Leftrightarrow m 0 Leftrightarrow m
0 Leftrightarrow m 0 Leftrightarrow m
Vậy m
b) Ta có: Hệ số
Điều kiện để hàm số là hàm bậc nhất là:
Vậy 1 thì hàm số đã cho là hàm số bậc nhất.
Bài 14
Hàm số bậc nhất y = (1 – √5)x – 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao?
b) Tính giá trị của y khi x = 1 + √5.
c) Tính giá trị của x khi y = √5
Gợi ý đáp án
a) Ta có a = 1- √5
b) Khi x = 1 + √5 ta có:
y = (1 – √5).(1 + √5) – 1 = (1 – 5) – 1 = -5
c) Khi y = √5 ta có:
√5 = (1 – √5)x – 1
=> √5 + 1 = (1 – √5)x
Lý thuyết Hàm số bậc nhất
1. Định nghĩa
– Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số thực cho trước và a ≠ 0
– Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x
2. Tính chất
a) Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R
b) Trên tập hợp số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a
Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x12 thì f(x1 ) 2 )
Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x12 thì f(x1 ) > f(x2 )
3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0)
a) Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0; nằm ở góc phần tư thứ II và thứ IV khi a
b) Đồ thị của hàm số y = ax + b là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0.
Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn gọi là đường thẳng y = ax + b; b được gọi là tung độ gốc của đường thẳng.

