Giải bài tập SGK Toán 9 Tập 1 trang 54, 55 để xem gợi ý giải các bài tập của Bài 4: Đường thẳng song song và đường thẳng cắt nhau thuộc chương 2 Đại số 9.
Bạn đang đọc: Giải Toán 9 Bài 4: Đường thẳng song song và đường thẳng cắt nhau
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 54, 55. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 4 Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Giải Toán 9 Bài 4: Đường thẳng song song và đường thẳng cắt nhau
Lý thuyết Đường thẳng song song và đường thẳng cắt nhau
1. Cho hai đường thẳng (d1 ): y = ax + b (a ≠ 0)
(d2 ): y =a’x + b’ (a’ ≠ 0)
+ (d1 ) // (d2 ) ⇔ a = a’; b ≠ b’
+ (d1 ) ≡ (d2 ) ⇔ a = a’; b = b’
+ (d1 ) cắt (d2 ) ⇔ a ≠ a’
2. Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn;
Khi a
3. Bổ sung
Cho hai đường thẳng (d1 ): y = ax + b (a ≠ 0)
(d2 ): y = a’x + b’ (a’ ≠ 0)
+ (d1 ) ⊥ (d2 ) ⇔ a.a’ = 1
+ Nếu (d1 ) cắt (d2 ) thì hoành độ giao điểm là nghiệm của phương trình ax + b = a’x + b’ (gọi là phương trình hoành độ giao điểm)
+ Góc α là góc tạo bởi đường thẳng y = ax + b và trục Ox. Nếu a > 0 thì tanα = a
Giải bài tập toán 9 trang 54, 55 tập 1
Bài 20 (trang 54 SGK Toán 9 Tập 1)
Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:
a) y = 1,5x + 2 ;
b) y = x + 2 ;
c) y = 0,5x – 3
d) y = x – 3 ;
e) y = 1,5x – 1 ;
g) y = 0,5x + 3
Gợi ý đáp án
– Các đường thẳng cắt nhau khi có a ≠ a’. Ta có ba cặp đường thẳng cắt nhau là:
a) y = 1,5x + 2 và b) y = x + 2 (vì có 1,5 ≠ 1)
a) y = 1,5x + 2 và c) y = 0,5x – 3 (vì có 1,5 ≠ 0,5)
a) y = 1,5x + 2 và d) y = x – 3 (vì có 1,5 ≠ 1)
…v…v……v…..v…..
– Các đường thẳng song song khi có a = a’ và b ≠ b’. Ta có các cặp đường thẳng song song với nhau là:
a) y = 1,5x + 2 và e) y = 1,5x – 1 (vì có 1,5 = 1,5 và 2 ≠ -1)
b) y = x + 2 và d) y = x – 3 (vì có 1 = 1 và 2 ≠ -3)
c) y = 0,5x – 3 và g) y = 0,5x + 3 (vì có 0,5 = 0,5 và -3 ≠ 3)
Bài 21 (trang 54 SGK Toán 9 Tập 1)
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5
Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
Gợi ý đáp án
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a’ = 2m + 1, b’ = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a’ phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay m ≠ 0 và m ≠
Theo đề bài ta có b ≠ b’ (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a’ tức là:
m = 2m + 1 => m = – 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có: m ≠ 0 và m ≠ và m ≠ -1.
Bài 22 (trang 55 SGK Toán 9 Tập 1)
Cho hàm số y = ax + 3. Hãy xác định hệ số a trong mỗi trường hợp sau:
a) Đồ thị của hàm số song song với đường thẳng y = -2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
Gợi ý đáp án
a) Theo đề bài ta có b ≠ b’ (vì 3 ≠ 0)
Vậy đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi a = a’ tức là:
a = -2.
Hàm số có dạng y = 2x + 3.
b) Thay x = 2, y = 7 vào hàm số y = ax + 3 ta được:
7 = a.2 + 3 => a = 2
Hàm số có dạng y = 2x + 3.
Giải bài tập toán 9 trang 55 tập 1: Luyện tập
Bài 23 (trang 55 SGK Toán 9 Tập 1)
Cho hàm số y = 2x + b. Hãy xác định hệ số b trong mỗi trường hợp sau:
a) Đồ thị của hàm số đã cho cắt trục tung tại điểm có tung độ bằng – 3.
b) Đồ thị của hàm số đã cho đi qua điểm A(1; 5).
Gợi ý đáp án
a) Đồ thị của hàm số y = 2x + b cắt trục tung tại điểm có tung độ bằng -3, nghĩa là khi x = 0 thì y = -3, do đó:
-3 = 2.0 + b => b = -3
b) Đồ thị hàm số y = 2x + b đi qua điểm (1; 5), do đó ta có:
5 = 2.1 + b => b = 3
Bài 24 (trang 55 SGK Toán 9 Tập 1)
Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k – 3. Tìm điều kiện đối với m và k để đồ thị của hai hàm số là:
a) Hai đường thẳng cắt nhau.
b) Hai đường thẳng song song với nhau.
c) Hai đường thẳng trùng nhau.
Gợi ý đáp án
Hàm số y = 2x + 3k có các hệ số a = 2, b = 3k.
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a’ = 2m + 1, b’ = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
⇔ m ≠
a) Hai đường thẳng cắt nhau khi a ≠ a’ tức là:
2 ≠ 2m + 1 ⇔ 2m ≠ 1
m ≠
Kết hợp với điều kiện trên ta có m = ±
b) Hai đường thẳng song song với nhau khi a = a’ và b ≠ b’ tức là:
2 = 2m + 1 và 3k ≠ 2k – 3
m = và k ≠ -3
Kết hợp với điều kiện trên ta có m = và k ≠ -3
c) Hai đường thẳng trùng nhau khi a = a’ và b = b’ tức là:
2 = 2m + 1 và 3k = 2k – 3
m = và k ≠ -3
Kết hợp với điều kiện trên ta có m = m = và k ≠ -3
Bài 25 (trang 55 SGK Toán 9 Tập 1)
a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt các đường thẳng theo thứ tự tại hai điểm M và N. Tìm tọa độ của hai điểm M và N.
Gợi ý đáp án
a) Hàm số
Cho
Cho y= 0
Đường thẳng đi qua hai điểm A, B là đồ thị của hàm số
+) Hàm số
Cho
Cho
Đường thẳng đi qua hai điểm A, C là đồ thị của hàm số
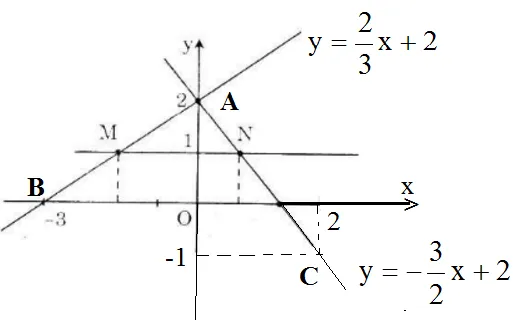
b) Đường thẳng song song với trục Ox cắt trục Oy tại điểm có tung độ 1 có dạng: y=1.
Vì M là giao của đường thẳng và y=1 nên hoành độ của M là nghiệm của phương trình:
Do đó tọa độ M là:
Vì N là giao của đường thẳng và y=1 nên hoành độ của N là nghiệm của phương trình:
Do đó tọa độ N là:
Bài 26 (trang 55 SGK Toán 9 Tập 1)
Cho hàm số bậc nhất y = ax – 4 (1). Hãy xác định hệ số a trong mỗi trường hợp sau:
a) Đồ thị của hàm số (1) cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2.
b) Đồ thị của hàm số (1) cắt đường thẳng y = -3x + 2 tại điểm có tung độ bằng 5.
Gợi ý đáp án
Hàm số y = ax – 4 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2 nên thay x = 2 vào phương trình hoành độ giao điểm ta có:
2a – 4 = 2.2 – 1 ⇔ 2a = 7 ⇔ a = 3,5
Kết hợp với điều kiện trên ta thấy a = 3,5 là giá trị cần tìm.
b) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = -3x + 2 tại điểm A có tung độ bằng 5 nên đường thẳng y = -3x + 2 đi qua điểm có tung độ bằng 5. Thay tung độ vào phương trình đường thẳng ta được hoành độ của giao điểm A là:
5 = -3x + 2 ⇔ – 3x = 3 ⇔ x = -1
Ta được A(-1; 5).
Đường thẳng y = ax – 4 cũng đi qua điểm A(-1; 5) nên ta có:
5 = a.(-1) – 4 ⇔ -a = 9 ⇔ a = -9
Kết hợp với điều kiện trên ta thấy a = -9 là giá trị cần tìm.

