Giải bài tập SGK Toán 9 Tập 1 trang 109, 110 để xem gợi ý giải các bài tập của Bài 4: Vị trí tương đối của đường thẳng và đường tròn thuộc chương 2 Hình học 9.
Bạn đang đọc: Giải Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 109, 110. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài Vị trí tương đối của đường thẳng và đường tròn Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Giải Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
Lý thuyết Vị trí tương đối của đường thẳng và đường tròn
1. Bảng tóm tắt
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
|
Đường thẳng và đường tròn cắt nhau Đường thẳng và đường tròn tiếp xúc nhau Đường thẳng và đường tròn không giao nhau |
2 1 0 |
d d = R d > R |
Trong đó, d là khoảng cách từ tâm đường tròn đến đường thẳng.
2. Dấu hiệu nhận biết tiếp tuyến
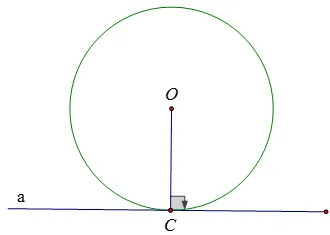
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
3. Tính chất của tiếp tuyến
Nếu một đường thẳng là một tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
4. Tính chất của hai tiếp tuyến cắt nhau.
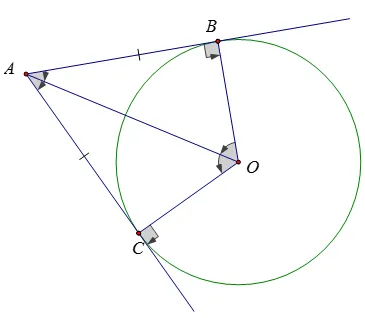
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
– Điểm đó cách đều hai tiếp điểm.
– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
5. Đường tròn nội tiếp tam giác
– Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
– Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân giác các góc trong của tam giác.
6. Đường tròn bàng tiếp tam giác
– Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.
– Tâm đường tròn bàng tiếp góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C.
Giải bài tập toán 9 trang 104 tập 1
Bài 17 (trang 109 SGK Toán 9 Tập 1)
Điền vào các chỗ trống (…) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):
| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 3cm | … |
| 6cm | … | Tiếp xúc nhau… |
| 4cm | 7cm | … |
Gợi ý đáp án
Từ hệ thức giữa d và R ta có bảng:
| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 3cm | Cắt nhau (d |
| 6cm | 6cm | Tiếp xúc nhau (d = R) |
| 4cm | 7cm | Không giao nhau (d > R) |
Bài 18 (trang 110 SGK Toán 9 Tập 1)
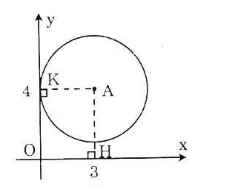
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
Bài 19 (trang 110 SGK Toán 9 Tập 1)
Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?
Gợi ý đáp án
Theo bài ra ta vẽ hình như sau:
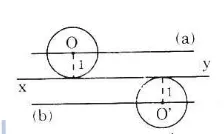
Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.
Ta có: R = 1, và đường tròn tiếp xúc với đường thẳng xy nên ta có: d = R, suy ra d = 1.
=> Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.
Bài 20 (trang 110 SGK Toán 9 Tập 1)
Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.
Gợi ý đáp án
Theo bài ra ta vẽ hình như sau:
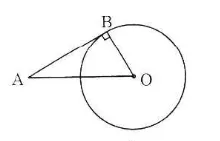
Xét đường tròn (O) có B là tiếp điểm nên OB=R=6cm.
Xét đường tròn (O) có AB là tiếp tuyến tại B nên AB bot OB tại B.
Xét vuông tại B, áp dụng định lý Pytago, ta có: