Download.vn Học tập Lớp 9 Toán 9

Bạn đang đọc: Hệ thức Vi-et: Lý thuyết, ứng dụng và các dạng toán

Hệ thức Vi-et: Lý thuyết, ứng dụng và các dạng toán Giải Toán 9

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Nhằm đem đến cho các bạn học sinh lớp 9 có thêm nhiều tài liệu học tập môn Toán, Download.vn giới thiệu chuyên đề Hệ thức Vi-et.

Chuyên đề Hệ thức Vi-et tổng hợp toàn bộ kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận, trắc nghiệm hệ thức Vi-ét. Qua tài liệu này giúp các bạn học sinh có thêm nhiều tư liệu tham khảo, tích lũy kiến thức biết giải các bài toán hệ thức Vi-ét để học tốt chương trình Toán 9.

Chuyên đề hệ thức Vi-ét và ứng dụng

CHUYÊN ĐỀ HỆ THỨC VI-ÉT VÀ ỨNG DỤNG A.TRỌNG TÂM CẦN ĐẠT I. TÓM TẮT LÝ THUYẾT 1. Hệ thức Vi-ét Cho phương trình bậc hai ax2+bx + c = 0 (a 0). Nếu x1, x2là hai nghiệm của phương trình thì: 1212..bSxxacPxxa2. Ứng dụng của hệ thức Vi-ét a) Xét phương trình bậc hai ax2+ bx + c = 0 (a ≠ 0). – Nếu a + b + c = 0 thì phương trình có một nghiệm là x1= 1, nghiệm còn lại là 2.cxa- Nếu a – b + c = 0 thì phương trình có một nghiệm là x1= -1, nghiệm còn lại là 2.cxab) Tìm hai số biết tổng và tích của chúng: Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình: X2- SX + P = 0. II. BÀI TẬP VÀ CÁC DẠNG TOÁN Dạng 1. Không giải phương trình, tính giá trị của biêu thức đối xứng giữa các nghiệm Phương pháp giải: Ta thực hiện theo các bước sau: Bước 1. Tìm điều kiện để phương trình có nghiệm: 0.0a Từ đó áp dụng hệ thức Vi-ét ta có: 12bSxxavà12..cPxxaBước 2. Biến đổi biểu thức đối xứng giữa các nghiệm của đề bài theo tổng x1+ x2và tích x1x2sau đó áp dụng Bước 1. Chú ý: Một số biểu thức đối xứng giữa các nghiệm thường gặp là: 22 2 212 12 12()2x 2;Axx xx xS P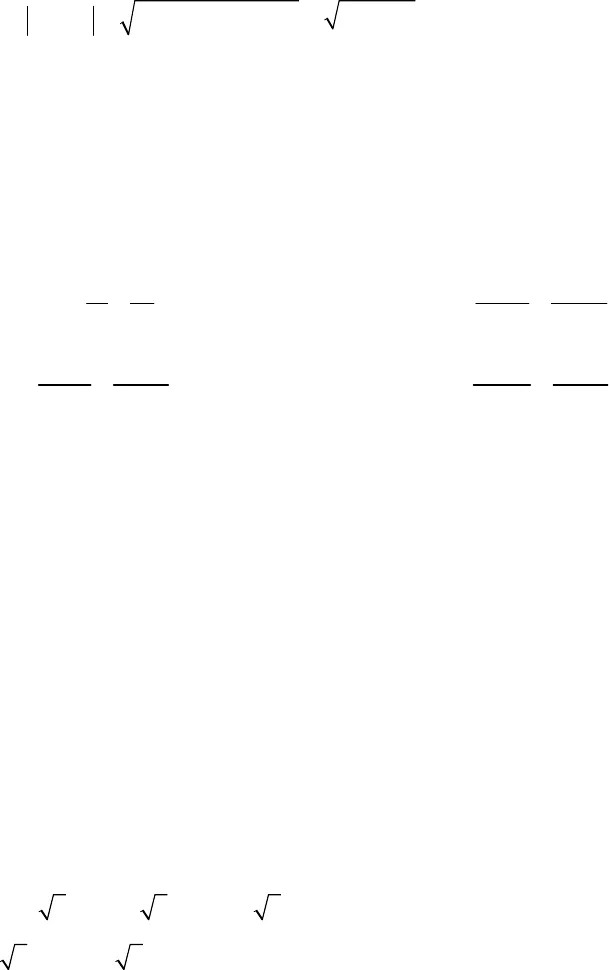      33 3 31 2 12 1212()3x() 3S;Bxx xx xxx S P       44 222 222 2 212 12 12()2x(2)2;Cx x x x xS P P      2212 12 12()4x 4.Dxx xx x S P      1.1. Gọi x1, x2là nghiệm của phương trình x2- 5x + 3 = 0. Không giải phương trình, hãy tính giá trị của các biểu thức: a)2212;Axx b)3312;Bxx1.2 .Cho phưoug trình: -3x2- 5x-2 = 0. Với x1,x2là nghiệm của phương trình, không giải phương trình, hãy tính:a)121211;Mxxxx  b)1211;33Nxxc)12221233;xxPxx d)1221.22xxQxx2.1.Cho phương trình x2- 2(m – 2)x + 2m -5 = 0 (ra là tham số). a) Tìm điều kiện của ra để phương trình có hai nghiệm phân biệt x1,x2.b) Với ra tìm được ở trên, tìm biểu thức liên hệ giữa x1,x2không phụ thuộc vào ra. 2.2. Cho phương trình x2+(m + 2)x + 2m = 0. Với giá trị nào của tham số m thì phương trình có hai nghiệm phân biệt x1,x2? Khi đó, hãy tìm biểu thức liên hệ giữa x1, x2không phụ thuộc vào ra.Dạng 2. Giải phương trình bằng cách nhấm nghiệm Phương pháp giải: Sử dụng ứng dụng của hệ thức Vi-ét. 3.1. Xét tổng a + b + c hoặc a – b + c rồi tính nhẩm các nghiệm của các phương trình sau: a) 15×2-17x + 2 = 0;b) 1230x2- 4x – 1234 = 0; c) (2 – 3 )x2+ 2 3 x – (2 + 3 ) = 0; d)25x- (2 – 5 )x – 2 = 0. 3.2. Tính nhẩm nghiệm của các phương trình sau: a) 7×2-9x + 2 = 0; b) 23×2-9x-32 = 0;c) 1975×2+ 4x – 1979 = 0; d) 31, 1×2- 50,9x + 19,8 = 0.4.1. Cho phương trình (ra – 2)x2- (2m + 5)x + ra + 7 = 0 với tham số ra. a) Chứng minh phương trình luôn có một nghiệm không phụ thuộc vào tham số m. 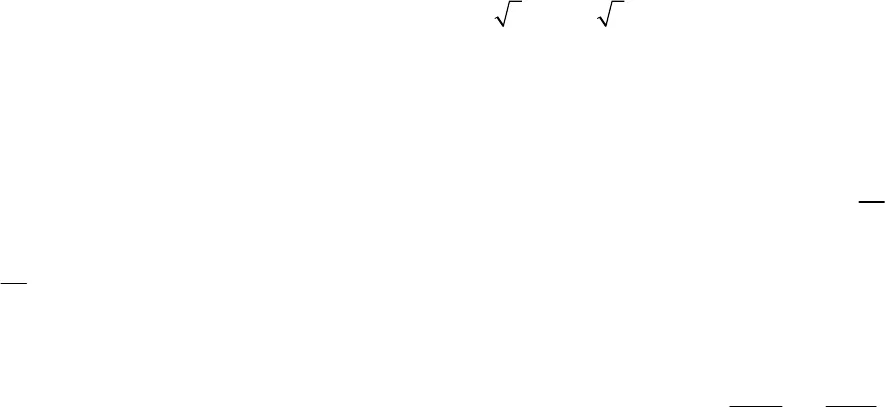b) Tìm các nghiệm của phương trình đã cho theo tham số ra. 4.2. Cho phương trình (2m – 1)x2+ (m – 3)x – 6m – 2 = 0.a) Chứng minh phương trình đã cho luôn có nghiệm x = -2. b) Tìm các nghiệm của phương trình đã cho theo tham số ra. 5.1. Cho phương trình mx2-3(m + l)x + m2- 13m – 4 = 0 (ra là tham số). Tìm các giá trị của ra để phương trình có một nghiệm là x = -2. Tìm nghiệm còn lại. 5.2. Tìm giá trị của tham số ra để phương trình x2+3mx – 108 = 0 (ra là tham số) có một nghiệm là 6. Tìm nghiệm còn lại. Dạng 3. Tìm hai số khi biết tổng và tích Phương pháp giải: Để tìm hai số x, y khi biết tổng S = x + y và tích P = x.y, ta làm như sau: Bước 1. Giải phương trình X2-SX+P = 0 để tìm các nghiệm X1,X2.Bước 2. Khi đó các số x, y cần tìm là x = X1,y = X2hoặc x = X2, y = X1.6.1. Tìm hai số u và v trong mỗi trường hợp sau: a) u + v = 15,uv = 36; b) u2+ v2= 13,uv = 6. 6.2. Tìm hai số u và v trong mỗi trường hợp sau: a) u + v = 4,uv = 7; b) u + v = -12,uv – 20. 7.1. Lập phương trình bậc hai có hai nghiệm là 2 + 3 và 2 – 3 . 7.2. Tìm phương trình bậc hai biết nó nhận 7 và -11 là nghiệm. 8.1.Cho phương trình x2+ 5x – 3m = 0 (m là tham số). a) Tìm tham số m để phương trình có hai nghiệm là x1và x2. b) Với điều kiện m tìm được ở câu a), hãy lập một phương trình bậc hai có hai nghiệm là 212xvà222x. 8.2. Cho phương trình 3x2+5x – m = 0. Với giá trị nào của tham số m, phương trình có hai nghiệm là x1và x2? Khi đó, hãy viết phương trình bậc hai có hai nghiệm là121xx và21.1xx Dạng 4. Phân tích tam thức bậc hai thành nhân tử Phương pháp giải: Nếu tam thức bậc hai ax2+ bx + c = 0 (a ≠ 0) có hai nghiệm x1; x2thì tamthức được phân tích thành nhân tử: ax2+ bx + c – a(x – x1)(x – x2).