Download.vn Học tập Lớp 10 Lớp 11 Toán 11

Bạn đang đọc: Hình không gian thể tích từ cơ bản đến nâng cao

Hình không gian thể tích từ cơ bản đến nâng cao Lý thuyết và bài tập thể tích trong Hình học không gian

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Nhằm đem đến cho các bạn học sinh lớp 11, 12 có thêm nhiều tài liệu học tập môn Toán, Download.vn xin giới thiệu tài liệu Hình không gian thể tích từ cơ bản đến nâng cao.

Đây là tài liệu vô cùng hữu ích, gồm 42 trang tóm tắt lý thuyết, công thức tính và hướng dẫn giải các dạng toán về thể tích của khối đa diện. Tài liệu phù hợp để các học sinh bị “mất gốc” ôn lại kỹ năng giải toán hình học không gian. Hy vọng với tài liệu này các bạn có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, thi THPT Quốc gia sắp tới. Mời bạn đọc cùng theo dõi và tải tại đây.

Hình không gian thể tích từ cơ bản đến nâng cao

http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan BẠN KHÔNG THÊTHAYĐÔI ĐICH ĐÊN NÊUBẠN KHÔNGĐÔI THAY CON ĐƯƠNG1HÌNH KHÔNG GIAN THỂ TÍCH TỪ CƠ BẢN ĐẾN NÂNG CAO FULL Giáo viên: Nguyễn Tiến ĐạtHÌNH KHÔNG GIAN THỂ TÍCHÔN TẬP 1: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 9 – 101. Hệ thức lượng trong tam giác vuông: Cho ABCvuông ởA. Ta có:a) Định lý Pitago :222BC AB ACb)22.; .BA BH BC CA CH CBc)..AB AC BC AHd)222111AH AB ACe)2BC AMf)sin ,cos , tan ,cotbcbcBBBBaacbg).sin .cos , .sin .cos ,sin cosba Ba CcabbBBaCCa   .tan .cotbc Bc C2. Hệ thức lượng trong tam giác thườngĐịnh lý hàm số côsin:2222.cosabc bc AĐịnh lý hàm số sin:2sin sin sinabcRABC3. Các công thức tính diện tícha)Công thức tính diện tích tam giác.11.sin22 4aabcSabCprppaapbpcRhvới2abcpĐặc biệt: ABCvuông ởA:1.2SABACABCđều cạnhABC:234aS b) Diện tích hình vuông: S cạnh x cạnhc) Diện tích hình chữ nhật: S dài x rộngd) Diện tích hình thoi:12S (chéo dài x chéo ngắn)ac bAMBCH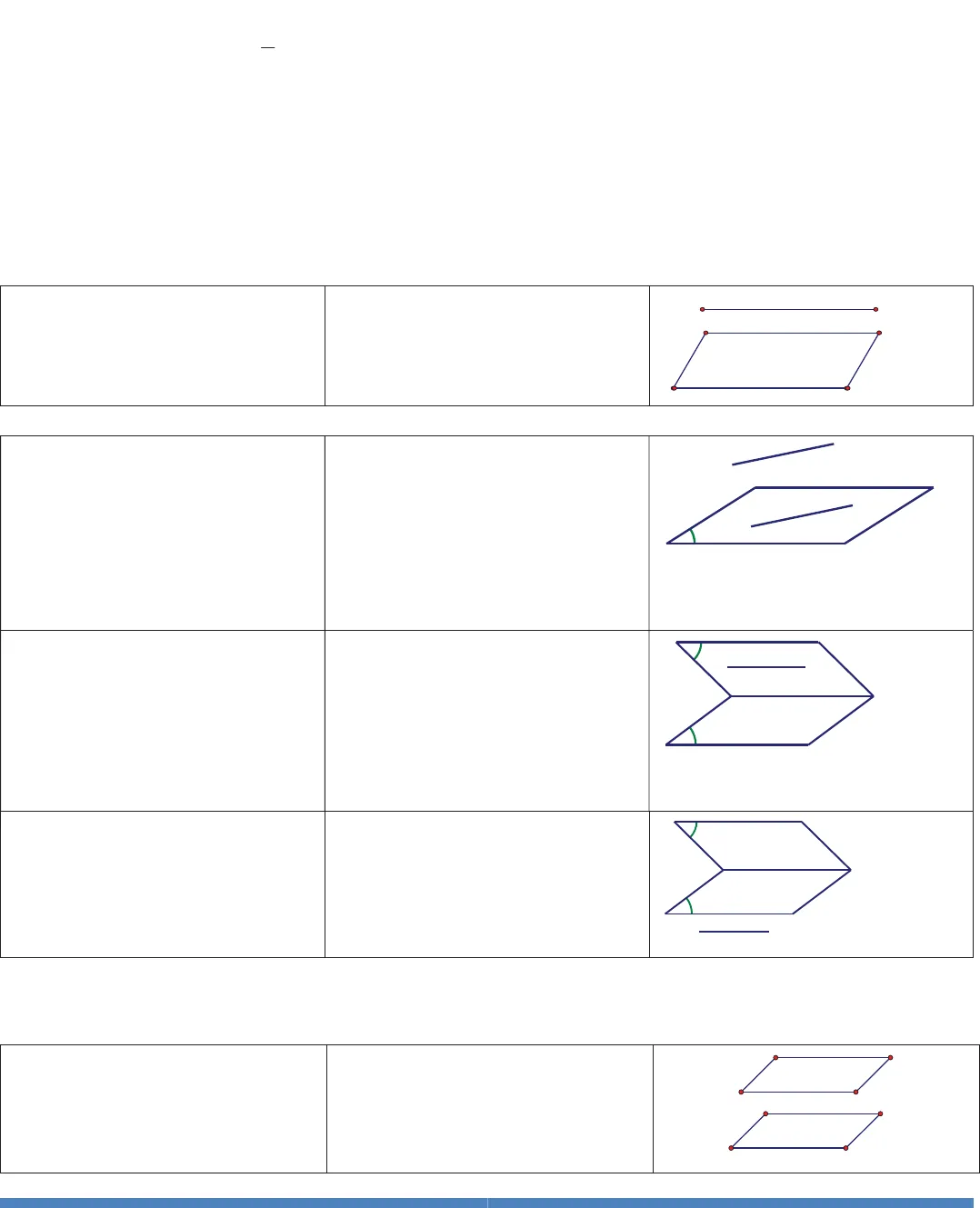http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan BẠN KHÔNG THÊTHAYĐÔI ĐICH ĐÊN NÊUBẠN KHÔNGĐÔI THAY CON ĐƯƠNG2e) Diện tích hình thang:12S (đáy lớn + đáy nhỏ) x chiều caof) Diện tích hình bình hành: S đáy x chiều caog) Diện tích hình tròn: 2SRÔN TẬP 2: KIẾN THỨC CƠ BẢN HÌNH HỌC LỚP 11A. QUAN HỆ SONG SONG§1.ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG1. Định nghĩaĐường thẳng và mặt phẳng gọi làsong song với nhau nếu chúngkhông có điểm nào chung.aP aP &2.Các định lý:Định lý 1: Nếu đường thẳng akhông nằm trên mặt phẳngvàsong song với một đường thẳngnào đó nằm trênthìasongsong với.aba ab&&Định lý 2: Nếu đường thẳng asong song với mặt phẳngP thìmọi mặt phẳngQ chứa amàcắtP thì cắt theo giao tuyếnsong song vớia.()aPaQ baPQb&&Định lý 3: Nếu hai mặt phẳng cắt nhau cùng song song với mộtđường thẳng thì giao tuyến củachúng cũng song song với đườngthẳng đó.PQbPa baQa&&&§2.HAI MẶT PHẲNG SONG SONG1. Định nghĩa:Hai mặt phẳng được gọi là songsong với nhau nếu chúng không cóđiểm nào chung.PQ PQ &a(P)αbaQPbaQPbaQP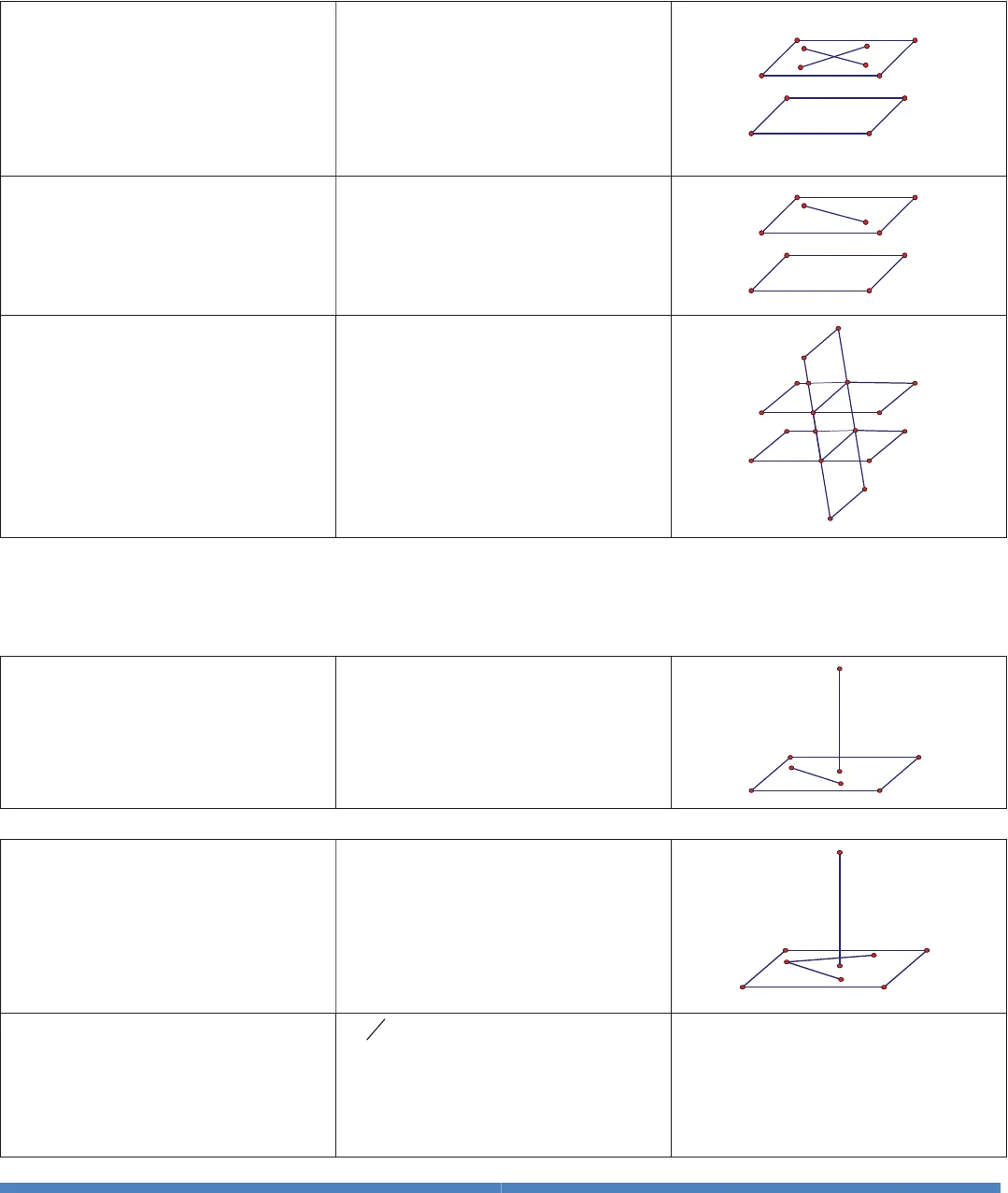http://www.toanmath.com/ Thầy NGUYỄN TIẾN ĐẠT https://www.facebook.com/thaydat.toan BẠN KHÔNG THÊTHAYĐÔI ĐICH ĐÊN NÊUBẠN KHÔNGĐÔI THAY CON ĐƯƠNG32. Các định lý:Định lý 1: Nếu mặt phẳng Pchứa hai đường thẳng a, b cắt nhauvà cùng song song với mặt phẳngQ thì PvàQsong songvới nhau.,,ab Pab I P QaQbQ &&&Định lý 2: Nếu một đường thẳng nằm một trong hai mặt phẳng songsong thì song song với mặt phẳngkia.PQaQaP&&Định lý 3: Nếu hai mặt phẳng PvàQ song song thì mọi mặtphẳngRđã cắtPthì phải cắtQvà các giao tuyến của chúngsong song. PQRPa abRQb&&B. QUAN HỆ VUÔNG GÓC§1.ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG1. Định nghĩa:Một đường thẳng được gọi làvuông góc với một mặt phẳng nếunó vuông góc với mọi đường thẳngnằm trên mặt phẳng đó.,aP accP2. Các định lý:Định lý 1: Nếu đường thẳng dvuông góc với hai đường thẳng cắtnhauavà b cùng nằm trong mặtphẳngP thì đường thẳng dvuông góc với mặt phẳngP .,,dadbab P d PabĐịnh lý 3: (Ba đường vuông góc) Cho đường thẳngakhông vuônggóc với mặt phẳngP và đườngthẳngb nằm trong P . Khi đó, ,’aPbPba baIbaQPaQPbaRQPPcadabP