Download.vn Học tập Lớp 12

Bạn đang đọc: Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC

Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC Tài liệu luyện thi THPT Quốc gia môn Toán

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC là tài liệu gồm 35 trang tuyển chọn 60 bài toán hàm số và đồ thị mức độ vận dụng và vận dụng cao trích từ các đề thi thử THPT Quốc gia môn Toán năm học 2018 – 2019.

Các bài toán được phân tích và hướng dẫn giải chi tiết. Tài liệu nhằm hỗ trợ các em trong quá trình ôn tập chuẩn bị cho kỳ thi THPT Quốc gia 2019 môn Toán. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Hướng dẫn giải 60 bài toán hàm số và đồ thị VD – VDC

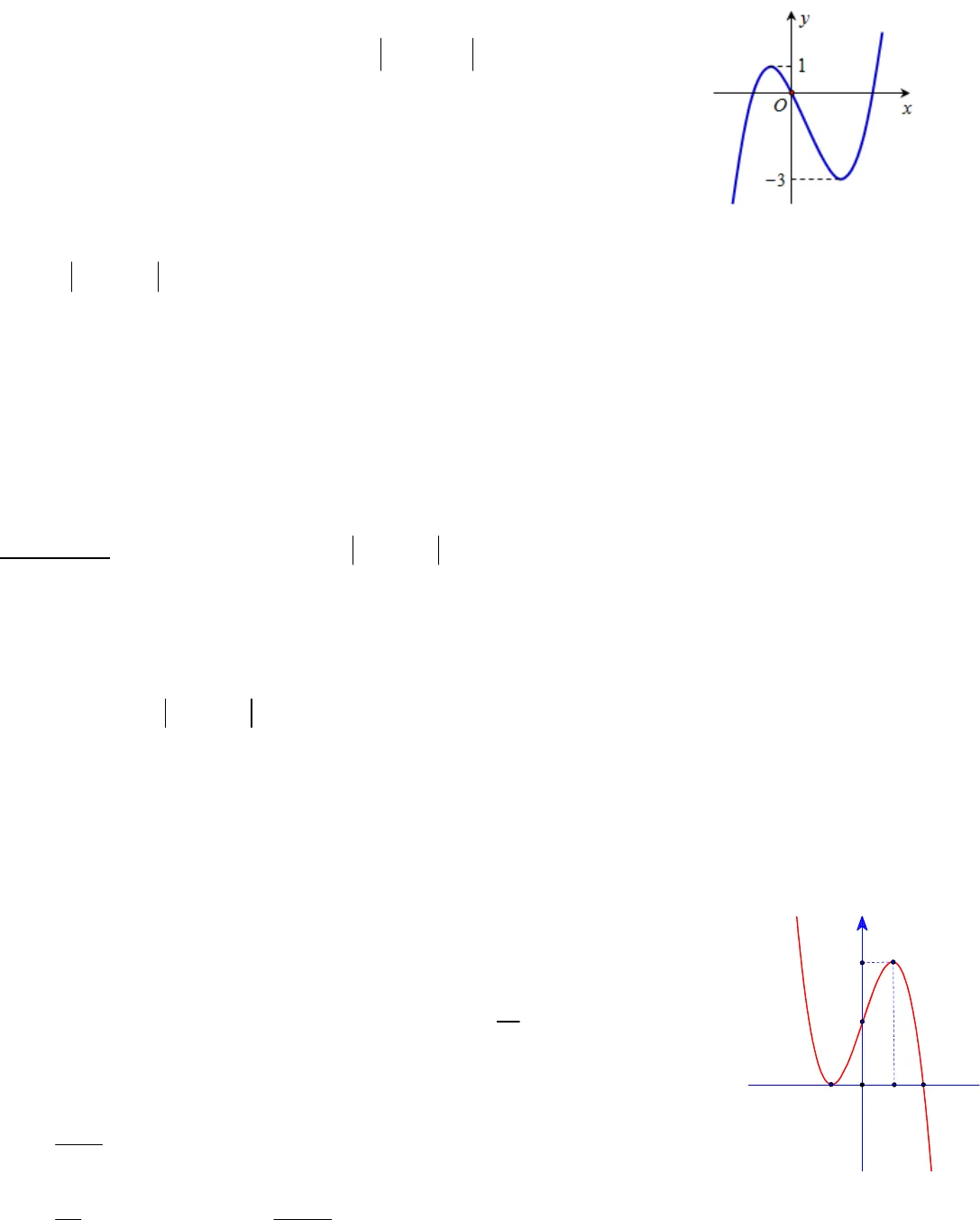1HÀM SỐ VD_VDCCâu 1: VD.Cho hàm số đa thức bậc ba yfxcó đồ thị như hình bên. Tìm tấtcả các giá trị của tham số m để hàm sốyfxmcó ba điểm cực trị.A. 1m  hoặc 3m  B. 3m  hoặc 1m  C.1m hoặc3m  D. 13m: Đáp án là A gồm và , trong đó có điểm cực trịcó 3 điểm cực trị có nghiệm đơn hoặc có nghiệm đơn và nghiệm kép .Trắc nghiệm: Số cực trị của hàm số bằng số cực trị của hàm số cộng số giao điểm của (không tính tiếp điểm)Hàm số có cực trịDo đó hàm số có cực trịphương trình có nghiệm đơn hoặc có nghiệm đơn và có nghiệm kép .Câu 2: VD.Cho hàm số yfxcó đạo hàmfx. Hàm sốyfxliên tụctrên tập số thực và có đồ thị như hình vẽ. Biết 131,264ff . Tổng giá trịlớn nhất và giá trị nhỏ nhất của hàm số33gx f x f xtrên1; 2bằng:A.157364 B. 198C.374 D. 1424564       12 0 0fxm khifxm LLy f x mfxmkhifxm L L1L2Lyfxm2L0fx m11131mm31mmyfxmyfxfxmyfx2yfxm3fxm11131mm31mmy22-114O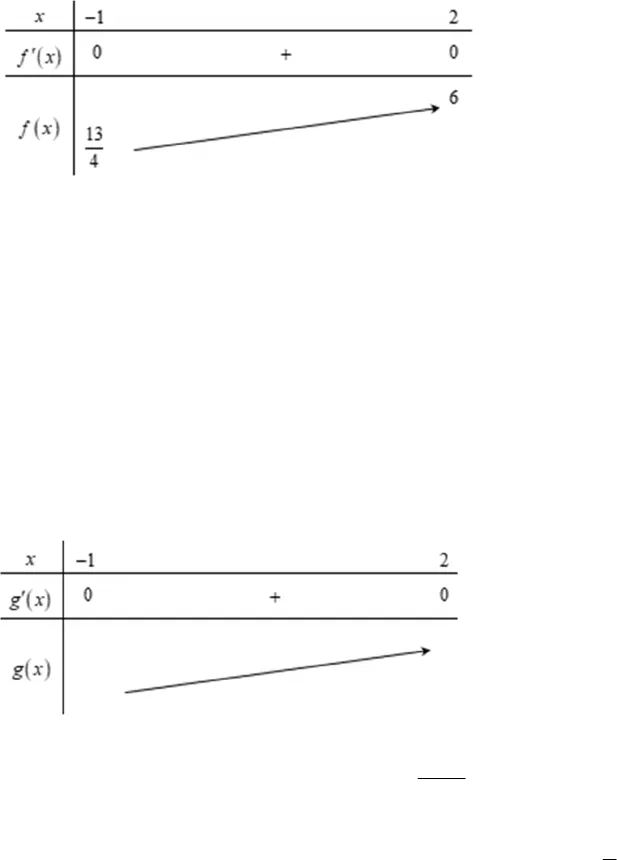2Đáp án là A Bảng biến thiênTa có .Xét trên đoạn . Bảng biến thiên.Câu 3 (VD): Gọi 12x,xlà hai điểm cực trị của hàm số321f(x) x 3x 2x3. Giá trị của2212xxbằng:A.13 B. 32 C. 4 D. 36 Cách giải:Ta có: 22f’ x x 6x 2 f’ x 0 x 6x 2 0  (*) Có12x;xlà hai điểm cực trị của đồ thị hàm số12yf(x) x,xlà hai nghiệm của phương trình (*).Áp dụng hệ thức Vi-et ta có:1212xx 6xx 222 2 212 12 12xx(xx)2xx62.(2)40   Chọn C.Câu 4 (VD): Biết rằng đồ thị hàm số 2332231 1 3 4ya xb xcxdcó hai điểm cực trị là (1;–7), (2:-8). Hãy xác định tổng222 2Mabcd.23. 3gx f xf x f x1; 20gx2310fx f x 0fx12xx   31;21573min 1 1 3 164gx g f f    3 A. -18 B. 18 C. 15 D. 8 Cách giải:Ta có22 3 2’33 1 2 1 3yaxbxcTừ giả thiết ta suy ra các điểm có tọa độ (1;-7), (2;-8) thuộc đồ thị hàm số đã cho và 1; 2xxlà hai điểm cựctrị của hàm số nên ta có hệ phương sau 23 223222 3 222 3 231.8 1.464 831.1 1.134 73. 3 1 .1 2. 1 3 03. 3 1 .2 2.2. 1 3 0ab cdabcdabcabc   Đặt23 231; 1;3; 4Aa Bb CcDd  ta được hệ mới 232842884282312773 1 91932 0 32 0 1231212 4 0 12 4 0 12412ABCD ABCD AaABCD A BC BbABC ABC CcABC ABC Dd          22222 222141849abMabcdcdChọn B.Câu 5 (VD): Tìm m để đường thẳng y2xmcắt đồ thị hàm sốx3yx1tại hai điểm M, N sao cho độ dàiMN nhỏ nhất:A.3B. -1 C. 2 D. 1 Cách giải:Phương trình hoành độ giao điểm của 2 đồ thị hàm số là:2x32x m x 1 2x (m 1)x m 3 0x1    (*)Ta có:222m 1 8(m 3) m 6m 25 (m 3) 16 0 m           (*) luôn có hai nghiệm phân biệt12x,xvới mọi m. Áp dụng hệ thức Vi-et ta có:1212m1xx2m3xx2Gọi11 2 2M(x ;2x m), N(x ;2x m)là hai giao điểm của 2 đồ thị hàm số.Khi đó ta có: