Download.vn Học tập Lớp 12
Bạn đang đọc: Hướng dẫn giải bài toán cực trị số phức
Hướng dẫn giải bài toán cực trị số phức Tài liệu ôn thi THPT Quốc gia 2019 môn Toán
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Dưới đây Download.vn xin giới thiệu đến quý thầy cô và các em học sinh, đặc biệt là học sinh lớp 12 tài liệu Hướng dẫn giải bài toán cực trị số phức.
Tài liệu gồm 11 trang trình bày 2 phương pháp giải bài toán cực trị số phức – một dạng toán số phức vận dụng cao trong chương trình Giải tích 12 chương 4. Tài liệu giúp thầy cô giáo có thêm nhiều tư liệu ra đề thi cũng như ôn luyện cho các em. Đồng thời giúp các em học sinh luyện và nâng cao kỹ năng giải toán. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Hướng dẫn giải bài toán cực trị số phức
Lương Đức Trọng – ĐHSPHN (SĐT:0982715678)CỰC TRỊ SỐ PHỨCA. TÓM TẮT LÝ THUYẾT1. Bất đẳng thức tam giác:• |z1+ z2| ≤ |z1| + |z2|, dấu “=” khi z1= kz2với k ≥ 0.• |z1− z2| ≤ |z1| + |z2|, dấu “=” khi z1= kz2với k ≤ 0.• |z1+ z2| ≥ ||z1| − |z2||, dấu “=” khi z1= kz2với k ≤ 0.• |z1− z2| ≥ ||z1| − |z2||, dấu “=” khi z1= kz2với k ≥ 0.2. Công thức trung tuyến: |z1+ z2|2+ |z1− z2|2= 2(|z1|2+ |z2|2)3. Tập hợp điểm:• |z −(a + bi)| = r : Đường tròn tâm I(a; b) bán kính r.• |z −(a1+ b1i)| = |z − (a2+ b2i)|: Đường trung trực của AB với A(a1; b1), B(a2; b2).• |z −(a1+ b1i)| + |z −(a2+ b2i)| = 2a:– Đoạn thẳng AB với A(a1; b1), B(a2; b2) nếu 2a = AB.– Elip (E) nhận A, B làm hai tiêu điểm với độ dài trục lớn là 2a nếu 2a > AB.Đặc biệt |z + c|+ |z − c| = 2a: Elip (E) :x2a2+y2b2= 1 với b =√a2− c2.B. CÁC DẠNG BÀI TẬPPhương pháp đại sốVÍ DỤ 1 (Sở GD Hưng Yên 2017). Cho số phức z thỏa mãn |z −1 −2i| = 4. Gọi M, m lầnlượt là giá trị lớn nhất, giá trị nhỏ nhất của |z + 2 + i|. Tính S = M2+ m2.A. S = 34 B. S = 82 C. S = 68 D. S = 36LỜI GIẢI 1. Ta có4 = |z + 2+ i −(3+ 3i)| ≥ ||z + 2 + i|−|3 + 3i|| = ||z + 2 + i|−3√2| ⇒(|z + 2 + i| ≤ 4 + 3√2 = M|z + 2 + i| ≥ 3√2 − 4 = m.Khi đó S = M2+ m2= 68.Đáp án là C.VÍ DỤ 2 (Sở GD Hà Tĩnh 2017). Trong các số phức z thỏa mãn |z − (2 + 4i)| = 2, gọi z1và z2là số phức có mô đun lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức z1và z2bằngA. 8i B. 4 C. −8 D. 81
https://www.facebook.com/luong.d.trongLỜI GIẢI. Ta có2 ≥ ||z| − |2 + 4i|| = ||z| − 2√5| ⇒ 2√5 − 2 ≤ |z| ≤ 2√5 + 2.Giá trị lớn nhất |z| là 2√5 − 2 khi z = k(2 + 4i) với (k − 1)√5 = 1 ⇒ k = 1 +1√5. Do đóz1=1 +1√5(2 + 4i).Giá trị nhỏ nhất |z| là 2√5 − 2 khi z = k(2 + 4i) với (1 − k)√5 = 1 ⇒ k = 1 −1√5. Do đóz2=1 −1√5(2 + 4i).Như vậy, tổng hai phần ảo của z1, z2là 41 +1√5+ 41 −1√5= 8.Đáp án là D.VÍ DỤ 3 (THPT Chuyên Thái Nguyên 2017 L3). Cho số phức z thỏa mãn |z2+ 4| = 2|z|.Kí hiệu M = max |z|, m = min |z|. Tìm mô đun của số phức w = M + mi.A. |w| = 2√3 B. |w| =√3 C. |w| = 2√5 D. |w| =√5LỜI GIẢI. Ta có2|z| ≥ |z|2− 4 ⇔ |z|2− 2|z| − 4 ≤ 0 ⇒ |z| ≤ 1 +√5 = M.và2|z| ≥ 4 − |z|2⇔ |z|2+ 2|z| − 4 ≥ 0 ⇒ |z| ≥ −1 +√5 = m.Vậy |w| =√M2+ m2= 2√3.Đáp án là A.VÍ DỤ 4 (THPT Yên Lạc-Vĩnh Phúc 2017). Trong các số phức z thỏa mãn |2z +z| = |z −i|,tìm số phức có phần thực không âm sao cho |z−1| đạt giá trị lớn nhất.A. z =√64+i2B. z =i2C. z =√34+i8D. z =√68+i8LỜI GIẢI. Gọi z = a + bi (a ≥ 0) thì z = a − bi. Khi đó√9a2+ b2=pa2+ (b − 1)2⇔ 2b = 1 − 8a2⇔ b =12− 4a2.Ta có |z−1| =1|z|lớn nhất khi và chỉ khi |z| =√a2+ b2nhỏ nhất.|z|2= a2+12− 4a22= 16a4− 3a2+14=4a2−382+764≥764⇒ |z| ≥√78.Do đó số phức z cần tìm thỏa mãna2=332⇒ a =√68b =12− 4a2=18. Vậy z =√68+i8.Đáp án là D.2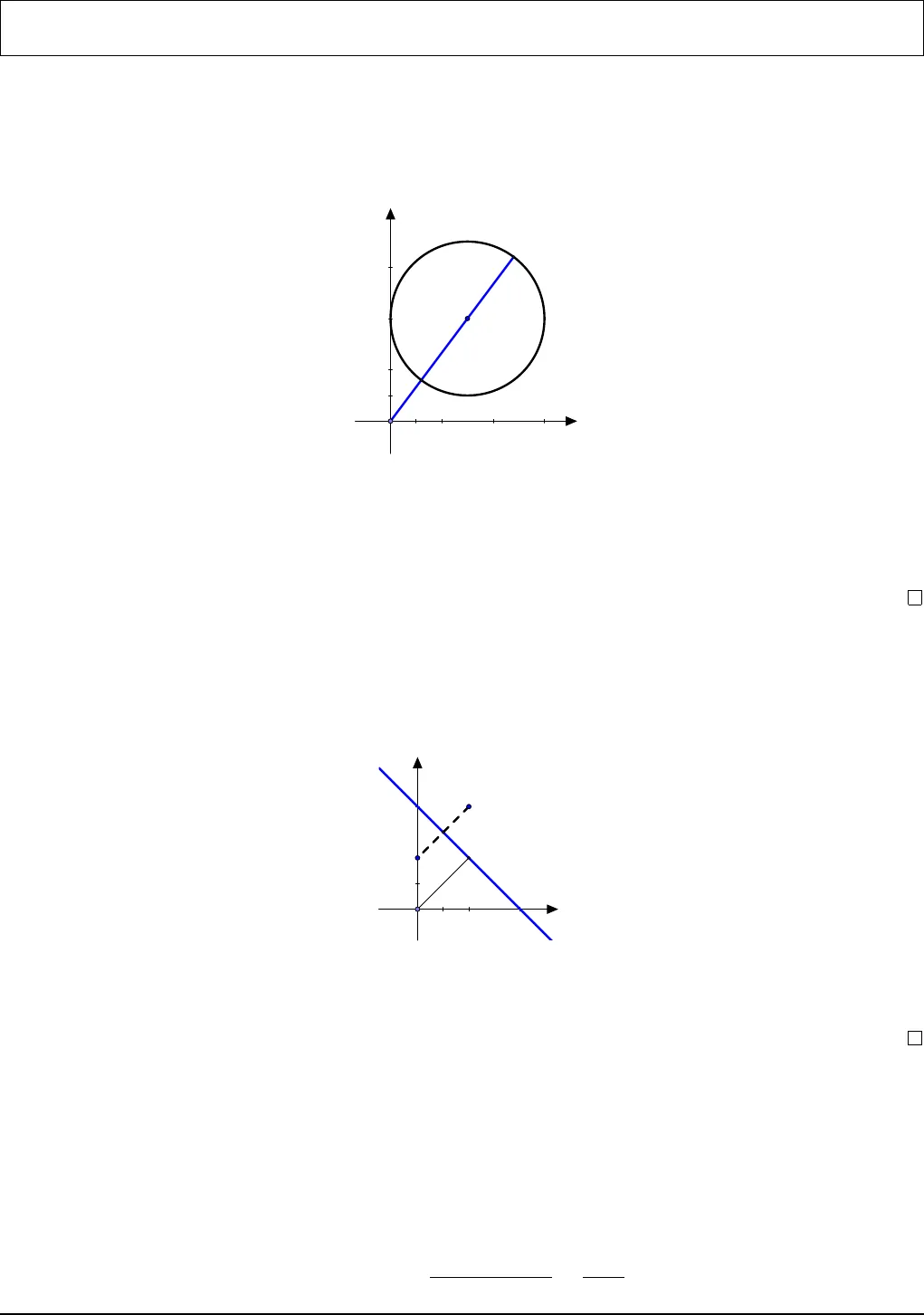
Lương Đức Trọng – ĐHSPHN (SĐT:0982715678)Phương pháp hình họcVÍ DỤ 5 (THPT Phan Bội Châu-Đăk Lăk 2017). Cho số phức z thỏa mãn |z −3−4i| = 1.Mô đun lớn nhất của số phức z là:A. 7 B. 6 C. 5 D. 4LỜI GIẢI.xyIOMNTập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(3; 4) bánkính r = 3. Khi đó |z| = OM với O là gốc tọa độ. Do đómax |z| = OI + r = 5 + 1 = 6.Đáp án là B.VÍ DỤ 6 (THPT Đồng Quan-Hà Nội 2017,THPT Chuyên Biên Hòa-Hà Nam 2017).Trong các số phức z thỏa mãn |z − 2 − 4i| = |z − 2i|. Tìm số phức z có mô đun nhỏ nhấtA. z = 2 − 2i B. z = 1 + i C. z = 2 + 2i D. z = 1 − iLỜI GIẢI.xyABIKOHGọi A(2; 4), B(0; 2), tập hợp các điểm z thỏa mãn giả thiết đề bài là đường trung trực dcủa AB có phương trình x + y −4 = 0. Khi đó |z| = OM nhỏ nhất khi M là hình chiếu củaO trên d là H(2; 2).Đáp án là C.VÍ DỤ 7 (THPT Trần Phú-Hà Nội 2017). Cho số phức z thỏa mãn |z + 3| + |z − 3| = 10.Giá trị nhỏ nhất của |z| làA. 3 B. 4 C. 5 D. 6LỜI GIẢI. Gọi A(−3; 0), B(3; 0) có trung điểm là O(0; 0). Điểm M biểu diễn số phức z. Theocông thức trung tuyến thì|z|2= MO2=MA2+ MB22−AB24.3