Download.vn Học tập Lớp 12
Bạn đang đọc: Hướng dẫn giải các dạng toán số phức
Hướng dẫn giải các dạng toán số phức Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Download.vn xin giới thiệu đến quý thầy cô giáo cùng các bạn học sinh lớp 12 tài liệu Hướng dẫn giải các dạng toán số phức. Đây là một chủ đề toán hay nhằm hỗ trợ các em trong quá trình học tập nội dung chương trình Giải tích 12 chương 4 và ôn tập chuẩn bị cho kì thi THPT Quốc gia.
Tài liệu gồm 104 trang phân dạng và hướng dẫn giải các dạng toán số phức thường gặp, trong mỗi dạng toán, tài liệu đều trình bày đầy đủ lý thuyết, hướng dẫn phương pháp giải toán, cùng với đó là các ví dụ minh họa và bài tập có lời giải chi tiết. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Hướng dẫn giải các dạng toán số phức
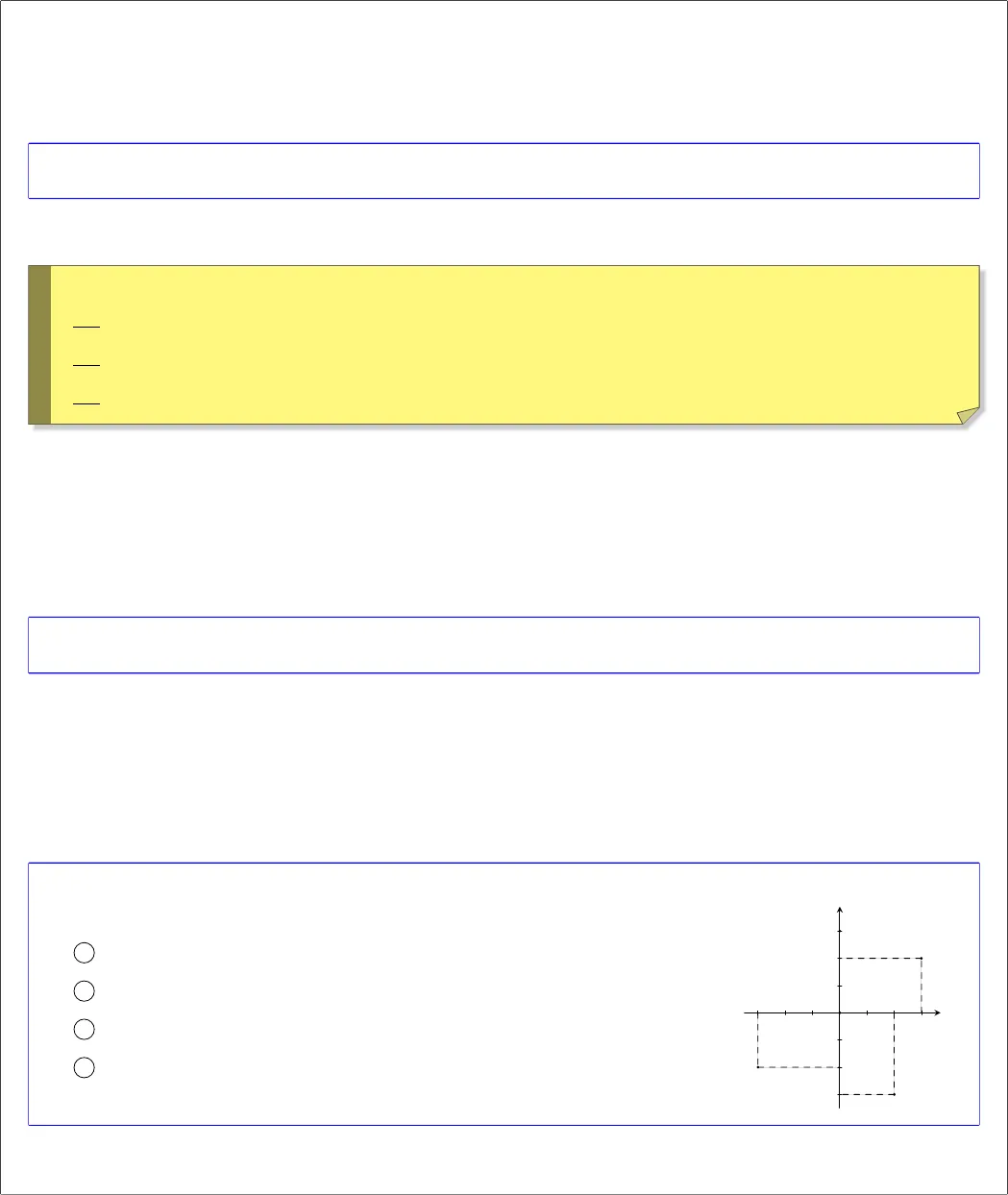LATEX PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/SỐ PHỨCBÀI 1. DẠNG ĐẠI SỐ CỦA SỐ PHỨC VÀ CÁC PHÉPTOÁN TRÊN SỐ PHỨCA. TÓM TẮT LÝ THUYẾT1. Định nghĩaĐịnh nghĩa 1. Mỗi biểu thức dạng a + bi, trong đó a, b ∈ R, i2= −1 được gọi là một số phức.Đối với số phức z = a + bi, ta nói a là phần thực, b là phần ảo của z, i gọi là đơn vị ảo.Tập số phức C = {a + bi|a, b ∈ R, i2= −1}. Tập số thực R ⊂ C.VÍ DỤ 1. Số phức z = 3 −2i có phần thực là ......phần ảo là ......Lời giải.Số phức z = 3 −2i có phần thực là 3 phần ảo là −2. !Đặc biệtKhi phần ảo b = 0 ⇔ z = a ∈ R ⇔ z là số thực.Khi phần thực a = 0 ⇔ z = bi ⇔ z là số thuần ảo.Số 0 = 0 + 0i vừa là số thực, vừa là số ảo.2. Hai số phức bằng nhauHai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.a + bi = c + di ⇔®a = cb = d, với a, b, c, d ∈ R.VÍ DỤ 2. Tìm các số thực x, y biết rằng (2x + 1) + (3y − 2)i = (x + 2) + (y + 4)i.Lời giải.Từ định nghĩa ta có®2x + 1 = x + 23y − 2 = y + 4⇔®x = 1y = 3.3. Biểu diễn hình học của số phứcĐiểm M(a; b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn của số phức z = a + bi.VÍ DỤ 3.Quan sát hình vẽ bên cạnh, ta có1 Điểm A biểu diễn cho số phức . . . . . . . . . . . . . . .2 Điểm B biểu diễn cho số phức ...............3 Điểm C biểu diễn cho số phức ...............4 Điểm D biểu diễn cho số phức ...............xy3A22B−3−3C−23DOLời giải.Ta có”Toán học là môn thể dục của trí tuệ “–Isocrates Trang 1
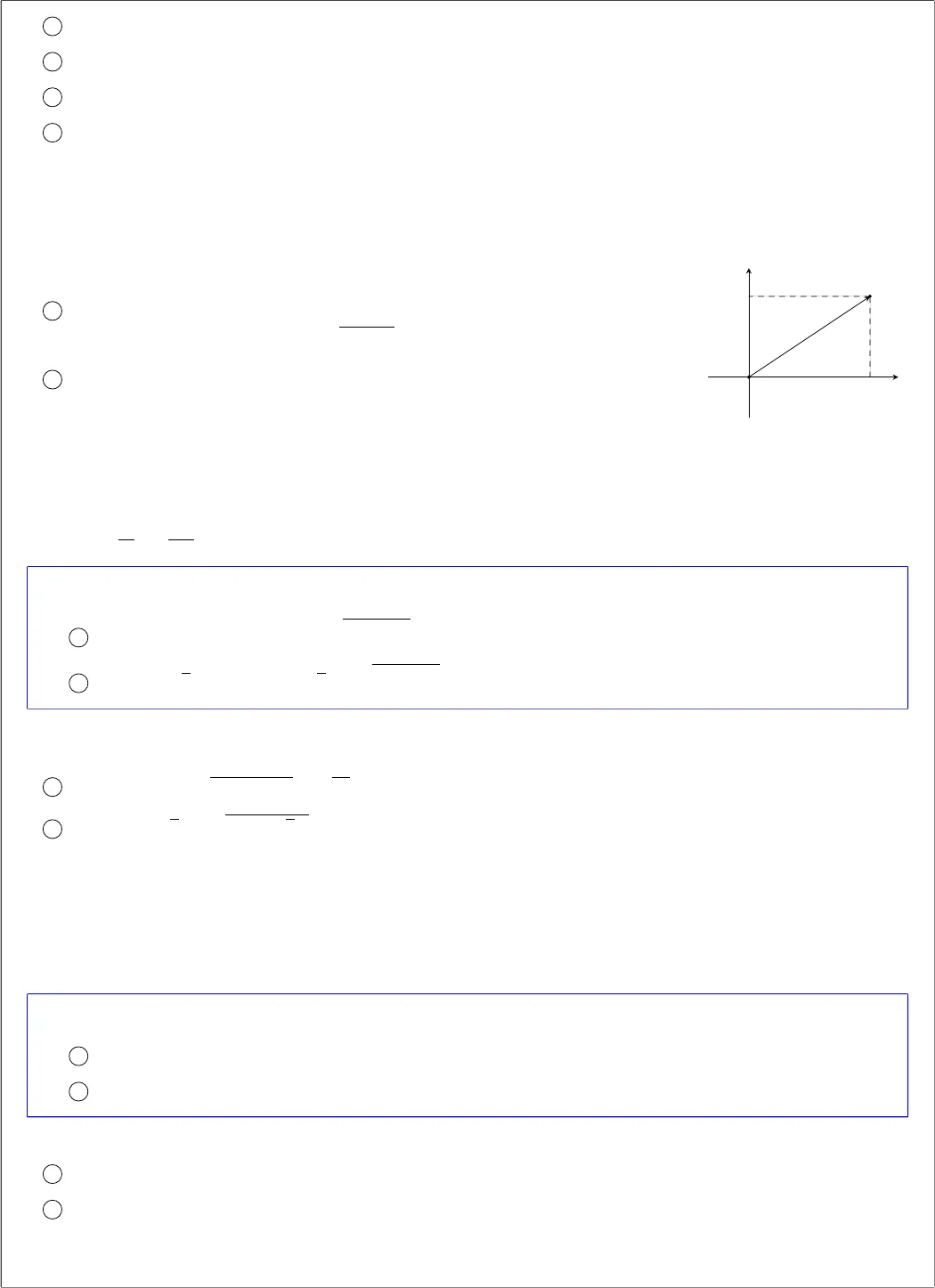PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/ LATEX1 Điểm A biểu diễn cho số phức z = 3 + 2i.2 Điểm B biểu diễn cho số phức z = 2 − 3i.3 Điểm C biểu diễn cho số phức z = −3 − 2i.4 Điểm D biểu diễn cho số phức z = 3i.4. Mô-đun của số phứcGiả sử số phức z = a + bi được biểu diễn bởi điểm M(a; b) trên mặt phẳng tọa độ.1 Độ dài của véc-tơ# »OM được gọi là mô-đun của số phức z và được ký hiệu là |z|.Khi đó, |z| =# »OM= |a + bi| =√a2+ b2.2 Kết quả, với mọi số phức z ta có(a) |z| ≥ 0 và |z| = 0 ⇔ z = 0.(b) z · ¯z = |z|2.(c) |z| = |¯z|.(d) |z1· z2| = |z1| · |z2|.(e)z1z2=|z1||z2|.xyaMbOVÍ DỤ 4. Tìm mô-đun của các số phức sau1 z = 3 − 2i ⇒ |z| = |3 − 2i| =». . . . . . . . . = . . . . . .2 z = 1 + i√3 ⇒ |z| = |1 + i√3| =». . . . . . . . . = . . . . . .Lời giải.Ta có1 |z| = |3 − 2i| =p32+ (−2)2=√13.2 |z| = |1 + i√3| =»12+ (√3)2= 2.5. Số phức liên hợpĐịnh nghĩa 2. Cho số phức z = a + bi, (a, b ∈ R). Ta gọi a − bi là số phức liên hợp của z và được ký hiệu là¯z = a − bi.VÍ DỤ 5.1 Cho z = −3 − 2i ⇒ ¯z = . . . . . . . . .2 Cho ¯z = 4 + 3i ⇒ z = . . . . . . . . .Lời giải.1 Cho z = −3 − 2i ⇒ ¯z = −3 + 2i.2 Cho ¯z = 4 + 3i ⇒ z = 4 − 3i.Trang 2 “Toán học là môn thể dục của trí tuệ “–Isocrates
LATEX PAGE TOÁN HỌC SƠ CẤP https://www.facebook.com/MATHDDT/Trên mặt phẳng tọa độ, các điểm biểu diễn z và ¯z đối xứng với nhau qua trụcOx.Từ định nghĩa ta có các kết quả sau2¯¯z = z; |¯z| = |z|.2 z1± z2= ¯z1± ¯z2.2 z1· z2= ¯z1· ¯z2.2Åz1z2ã=¯z1¯z2.2 z là số thực ⇔ z = ¯z.2 z là số thuần ảo ⇔ z = −¯z.xyaz = a + bib¯z = a − bi−bO6. Cộng, trừ, nhân, chia số phứcCho hai số phức z1= a + bi và z2= c + di.1 Phép cộng và phép trừ hai số phức được thực hiện theo quy tắc cộng, trừ đa thức.Phép cộng: z1+ z2= (a + bi) + (c + di) = (a + c) + (b + d)i.Phép trừ: z1− z2= (a + bi) − (c + di) = (a − c) + (b −d)i.Số phức đối của của số phức z = a + bi là −z = −a − bi. Do đó, z + (−z) = (−z) + z = 0.VÍ DỤ 6. Cho hai số phức z1= 5 + 2i và z2= 3 + 7i. Tìm phần thực, phần ảo và mô-đun của số phứcw = z1+ z2và số phức w0= z2− z1.Lời giải.Ta có w = (5 + 2i) + (3 + 7i) = 8 + 9i và w0= (3 + 7i) − (5 + 2i) = −2 + 5i.Như thế• w có phần thực là 8, phần ảo là 9 và mô-đun là |w| =√82+ 92=√145,• w0có phần thực là −2, phần ảo là 5 và mô-đun là |w0| =p(−2)2+ 52=√29.2 Phép nhân số phức được thực hiện theo quy tắc nhân đa thức, rồi thay i2= −1 trong kết quả nhận được.Cụ thể, z1· z2= (ac − bd) + (ad + bc)i.3 Phép chia:z1z2=z1· ¯z2z2¯z2=z1· ¯z2|z2|2=ac + bdc2+ d2+bc − adc2+ d2· i, (z26= 0).4 Số phức nghịch đảo của z = a + bi 6= 0 là1z=¯z|z|2=¯za2+ b2=a − bia2+ b2.VÍ DỤ 7. Cho hai số phức z1= 5 + 2i và z2= 4 + 3i. Hãy tính• w = z1· z2= . . . . . ........ . . . . . . . . . . . .. . . . . .. . . . . . .. . . . . .. . . . . . . . . . . . .. . . . . .. . . . . . . . . . . . .. . . . .• z1· ¯z2= . . . .. . . . . . .. . . . . .. . . . . . . . . . . . .. . . . . .. . . . . . . . . . . . .. . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . .. . . . .• r =z1z2= .. . . . . .. . . . . . .. . . . . .. . . . . .. . . . . . . . . . . . .. . . . . .. . . . . . .. . . . . .. . . . . . . . . . . . .. . . . . .. . . . . . . .Lời giải.Ta có• w = z1· z2= (5 + 2i)(4 + 3i) = 14 + 23i.• z1· ¯z2= (5 + 2i)(4 − 3i) = 26 − 7i = 26 + 7i.• r =z1z2=5 + 2i4 + 3i=(5 + 2i)(4 − 3i)(4 + 3i)(4 − 3i)=26 − 7i25=2625−725· i.”Toán học là môn thể dục của trí tuệ “–Isocrates Trang 3