Download.vn Học tập Lớp 12

Bạn đang đọc: Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Mời quý thầy cô cùng các bạn học sinh lớp 12 tham khảo tài liệu Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao được Download.com.vn đăng tải ngay sau đây.

Đây là tài liệu vô cùng hữu ích, hướng dẫn giải 65 bài toán số phức hay và khó, các bài toán số phức liên quan đến min – max, bất đẳng thức. Sau đây là nội dung chi tiết mời các bạn cùng tải tài liệu tại đây.

Hướng dẫn giải một số bài tập số phức mức độ vận dụng cao

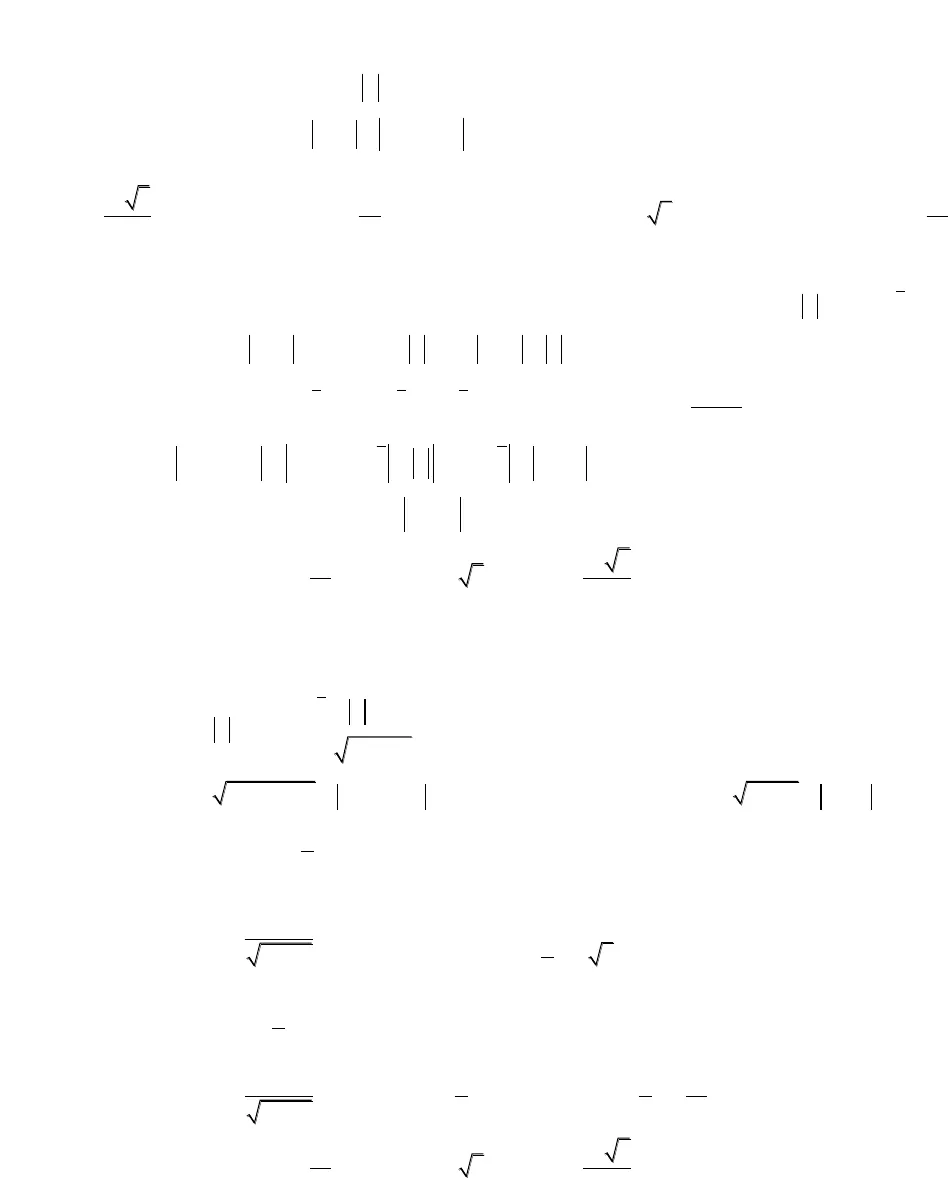Bài 1: Cho số phức z thỏa mãn 1z . Gọi M và m lần lượt là giá trị lớn nhất và giá trịnhỏ nhất của biểu thức211P z z z    . Tính giá trị của M.n A. 13 34B.394C.33D.134 Cách 1:Re( )zlà phần thực của số phức z, Im(z) là phần ảo của số phức z,1 . 1  z z z Đặt 1tz, ta có:0 1 1 1 2 0;2z z z t          2221 1 1 . 2 2Re( ) Re( )2tt z z z z z z z z          2 2 21 . 1 3z z z z z z z z z t          Xét hàm số:  23 , 0;2f t t t t    . Xét 2 TH: 134Maxf t ; 3Minf t 13 3.4Mn Cách 2: cos sinz r x i x a bi    Do222.111z z zzr a b  2 2cos 2cos 1P x x   , đặt  cos 1;1tx   2 2 2 1f t t t     TH1: 11;2t     131′ 2 013222maxf t fftminf t ft      TH1: 1;12t   1 7 7 13′ 2 08 8 422f t t maxf t ft          134Maxf t ; 3Minf t 13 3.4Mn———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————-Hướng dẫn giải một số bài tập số phức mức độ vận dụng caoBiên soạn: Phạm Minh Tuấn – TOANMATH.com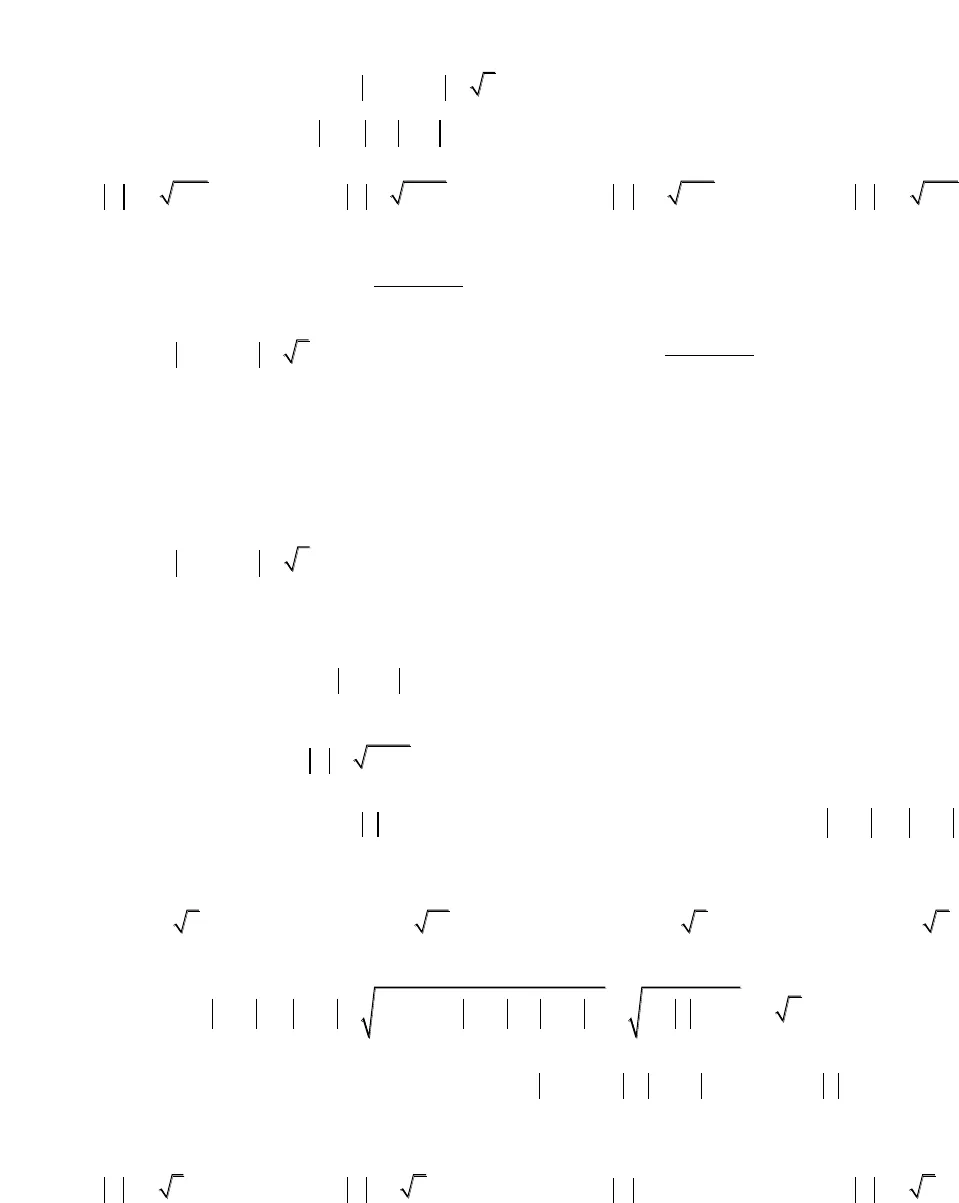Bài 2: Cho số phức z thỏa mãn 3 4 5zi  . Gọi M và m là giá trị lớn nhất và giá trịnhỏ nhất của biểu thức 222P z z i   . Tính module số phức w M mi.A. 2 314w B.1258w C.3 137w D.2 309w  Cách 1:434 2 32PxP x y y           22 2 2433 4 5 3 4 5 3 4 52Pxz i x y x f x                  ’ 8 3 8 4 11 0 0,2 1,6 0,1 1,7f x x P x x P y P            Thay vào  fxta được:   22330,2 1,6 3 0,1 1,7 4 5 013PPPP        Cách 2:     223 4 5 3 4 5:z i x y C       ( ):4 2 3 0x y P     Tìm P sao cho đường thẳng và đường tròn Ccó điểm chung ; 23 10 13 33d I R P P         Vậy 33MaxP ;13MinP 33 13 1258w i w   Bài 3: Cho số phức z thỏa mãn 1z. Tìm giá trị lớn nhất của biểu thức 1 2 1P z z   .A. max25PB.max2 10PC.max35PD.max32P Giải: Theo BĐT Bunhiacopxki: 2 2 2221 2 1 1 2 1 1 10 1 2 5P z z z z z           Bài 4: Cho số phức z x yi ,x y Rthỏa mãn2 4 2z i z i   vàm min z. Tínhmodule số phức  w m x y i  .A. 23w B.32w C.5w D.26w ———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————-Hướng dẫn giải một số bài tập số phức mức độ vận dụng caoBiên soạn: Phạm Minh Tuấn – TOANMATH.com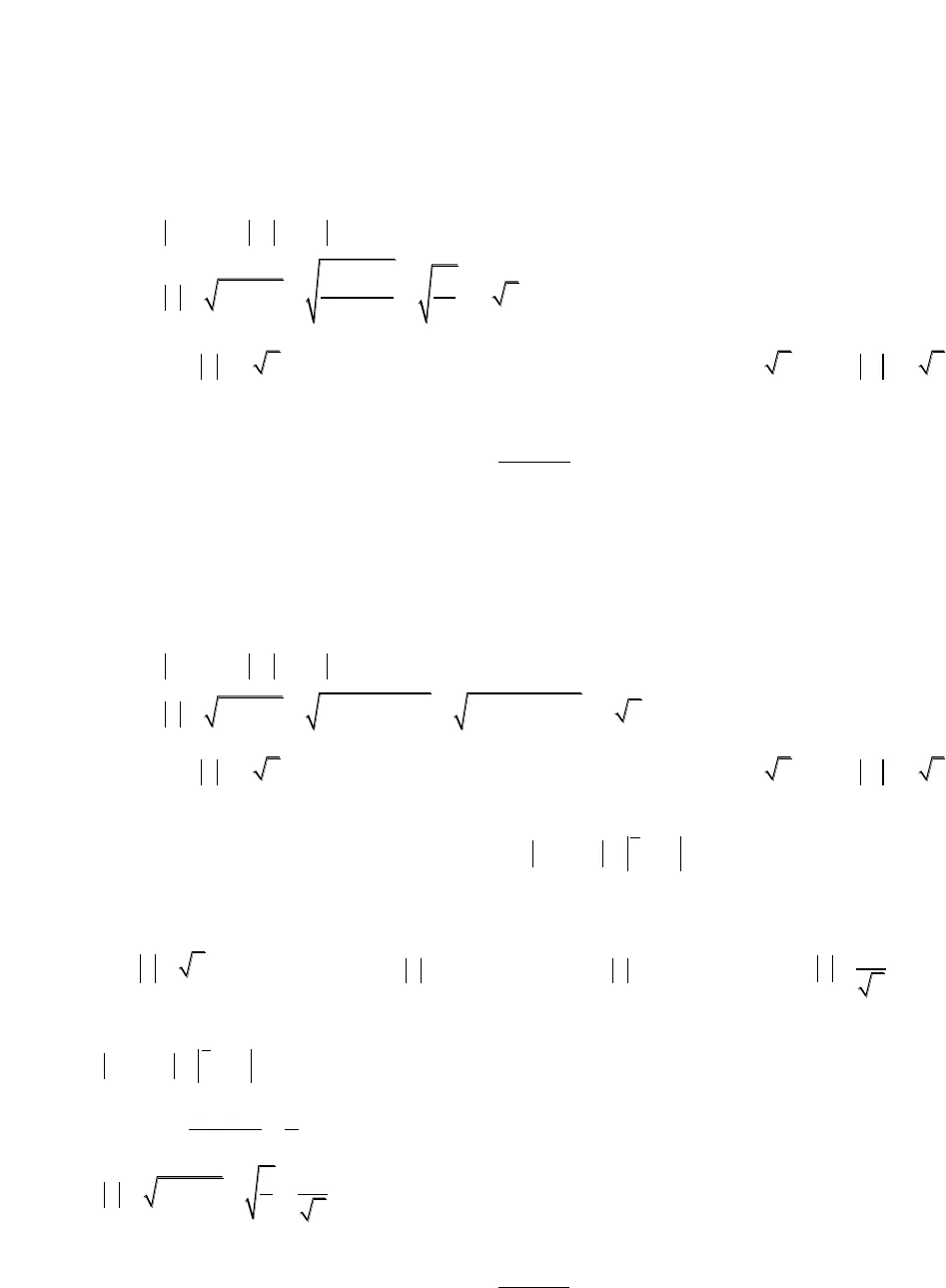 Cách 1:2 4 2 4z i z i x y       222242222xyz x y    22min z , Dấu “=” xảy ra khi42w 2 2 4 w 2 62x y xix y y       Chú ý: Với mọi x, y là số thực ta có:  2222xyxyDấu “=” xảy ra khixy Cách 2:2 4 2 4z i z i y x         222 2 24 2 2 8 2 2z x y x x x        22min z . Dấu “=” xảy ra khi42w 2 2 4 w 2 622x y xixy       Bài 5: Cho số phức z x yi ,x y Rthỏa mãn 12z i z i   . Tìm môđun nhỏ nhất của z.A.2min z B.1min z C.0min z D.12min z  Cách 1:1 2 1z i z i x y       222122xyxy  221122z x y   Chú ý: Với mọi x, y là số thực ta có:  2222xyxy Cách 2:———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————-Hướng dẫn giải một số bài tập số phức mức độ vận dụng caoBiên soạn: Phạm Minh Tuấn – TOANMATH.com