Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Lý thuyết và bài tập chuyên đề giới hạn

Lý thuyết và bài tập chuyên đề giới hạn Tổng hợp lý thuyết và bài tập chuyên đề giới hạn

Giới thiệu Tải về Bình luận

• 5

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Lý thuyết và bài tập chuyên đề giới hạn là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo.

Tài liệu gồm 75 trang tóm tắt lý thuyết chuyên đề giới hạn và tuyển chọn bài tập tự luận, trắc nghiệm giới hạn dãy số, giới hạn hàm số và hàm số liên tục có đáp án và lời giải chi tiết giúp học sinh học tốt chương trình Đại số và Giải tích 11 chương 4. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tại đây.

Tổng hợp lý thuyết và bài tập chuyên đề giới hạn

MỤC LỤCPHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN§1. GIỚI HẠN CỦA DÃY SỐ 01 – 14 §2. GIỚI HẠN CỦA HÀM SỐ 15 – 31 §3. HÀM SỐ LIÊN TỤC 32 – 40 ÔN TẬP CHƯƠNG IV 41 – 49PHẦN II. TRẮC NGHIỆM GIỚI HẠN CỦA DÃY SỐ 50 – 54GIỚI HẠN CỦA HÀM SỐ 55 – 59HÀM SỐ LIÊN TỤC 60 – 62ÔN TẬP CHƯƠNG IV. GIỚI HẠN 63 – 72ĐÁP ÁN TRẮC NGHIỆM 73 – 74 Toán 11 GV. Lư Sĩ Pháp1BT. ĐS&GT 11 Chương IV. Giới hạnCHƯƠNG IV.GIỚI HẠN PHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN§1. GIỚI HẠN CỦA DÃY SỐ A. KIẾN THỨC CẤN NẮM 1. Giới hạn hữu hạn của dãy số nnulim 0→+∞=khi và chỉ khinucó thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trởđi.  n nn nv a v alim lim ( ) 0→+∞ →+∞= ⇔ − = Dãy số (un) có giới hạn 0 khi và chỉ khi dãy số()nucó giới hạn 0 2. Giới hạn vô cực nnulim→+∞= +∞khi và chỉ khinucó thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đótrở đi. Kí hiệu: n nu hay u khi nlim= +∞ → +∞ → +∞ Dãy số (nu) được gọi là có giới hạn−∞khin→ +∞nếunulim( )− = +∞ Nhận xét: n nn nu ulim lim ( )→+∞ →+∞= +∞ ⇔ − = −∞;n nn nu ulim lim ( )→+∞ →+∞= −∞ ⇔ − = +∞Lưu ý: Thay cho viếtn nn nu L ulim , lim→+∞ →+∞= = ±∞, ta viếtn nu a ulim ,lim= = ±∞3. Các giới hạn đặc biệt a) n1lim 0=; kn1lim 0=; knlim= +∞, với k nguyên dương. b) nqlim 0=, nếuq1 nqlim= +∞nếu q > 1 c) c clim=; kcnlim 0=, lim(c un) = climun, với c là hằng số,k*∈ℕd) nnqlim 0=nếuq1>4. Định lí về giới hạn hữu hạnĐịnh lí 1. Nếunu Llim=vànv Mlim=, thì:  n n n nu v u v L Mlim( ) lim lim+ = + = + n n n nu v u v L Mlim( ) lim lim− = − = − n n n nu v u v L Mlim . lim .lim .= =  nc u c Llim( . ) .= ( với c là hằng số)  nnuLv Mlim = (nếu M0≠)Định lí 2. Giả sử nu Llim= Nếu nu0≥với mọi n thìL0≥vànu Llim = nu Llim=vànu L33lim = Nếu nulim= +∞thìnu1lim 0=5. Một vài quy tắc tìm giới hạn vô cực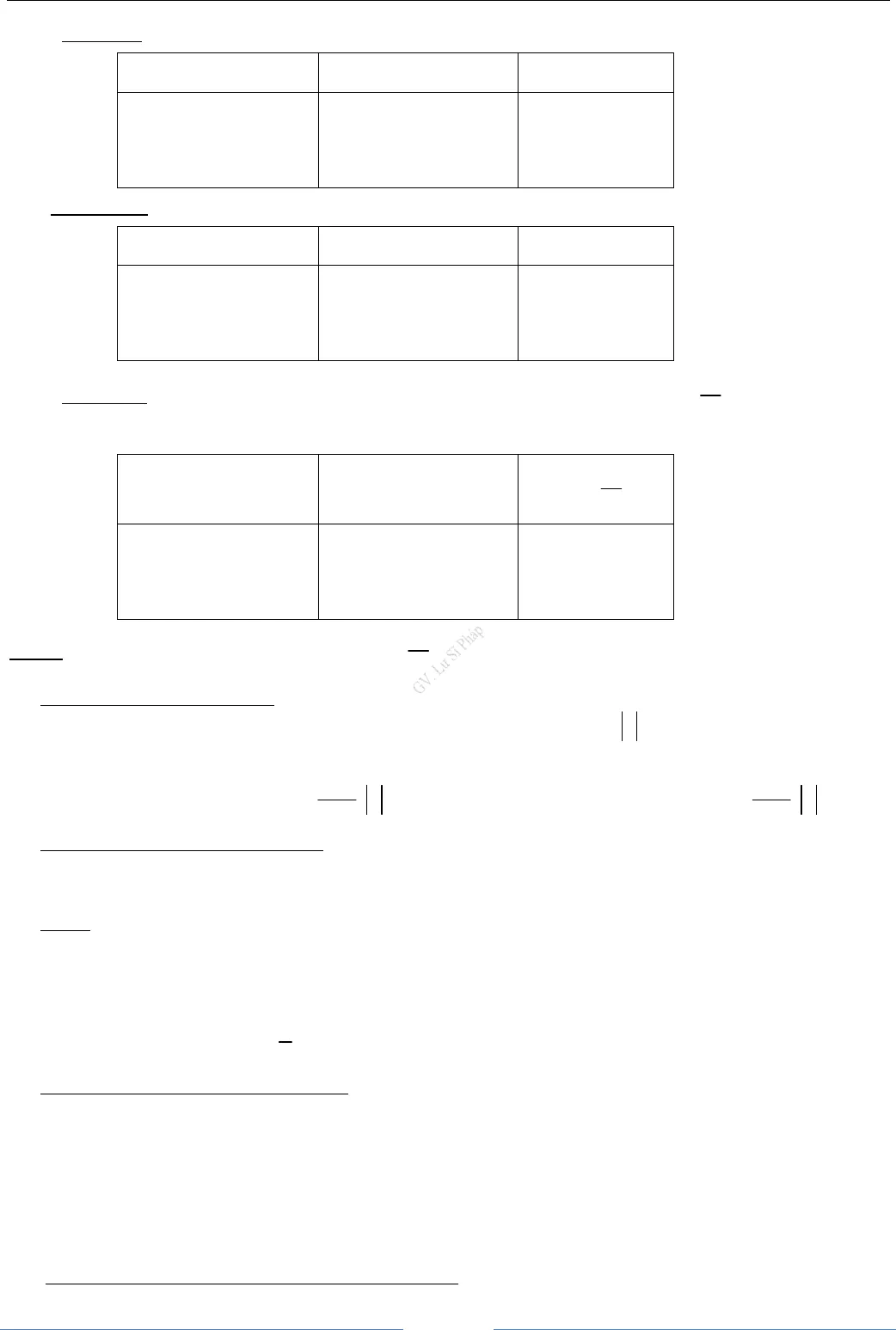Toán 11 GV. Lư Sĩ Pháp2BT. ĐS&GT 11 Chương IV. Giới hạna) Quy tắc 1. Nếunulim= ±∞vànvlim= ±∞thì()n nu vlimđược cho trong bảng:nulimnvlim()n nu vlim+∞+∞−∞−∞+∞−∞+∞−∞+∞−∞−∞+∞b) Quy tắc 2. Nếunulim= ±∞vànv Llim 0= ≠thì()n nu vlimđược cho trong bảng:nulimDấu của L()n nu vlim+∞+∞−∞−∞+−+−+∞−∞−∞+∞c) Quy tắc 3. . Nếunu Llim 0= ≠vànvlim 0=vànv0>hoặcnv0    được cho trongbảng:Dấu của LDấu củanvnnuvlim    ++−−+−+−+∞−∞−∞+∞Chú ý . Nếu n nu L vlim 0,lim= > = ±∞thìnnuvlim 0=6. Tổng cấp số nhân lùi vô hạn Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa mãn q1 Công thức tính tổng S của cấp số nhân lùi vô hạn (un)nuS u u u u qq11 2 3… ... ; 11= + + + + + = u u q u q u q qq2 111 1 1 1… … ; 11−= + + + + + = Định lí kẹp về giới hạn của dãy sốCho ba dãy số (un), (vn) ,(wn) và số thực L. Nếun n nu v w≤ ≤với mọi n và lim un= lim wn= L thì dãy số (vn) có giới hạn và lim vn= L.8. Lưu ý a) Dãy số tăng và bị chặn trên thì có giới hạnb) Dãy số giảm và bị chặn dưới thì có giới hạn c) Nếu limun= a thì limun + 1= ad) Số e:nnen1lim 1→+∞ = +  9. Phương pháp tìm giới hạn của dãy số– Vận dụng nội dung định nghĩa– Tìm giới hạn của một dãy số ta thường đưa về các giới hạn dạng đặc biệt và áp dụng các định lí về giới hạn hoặc các định lí về giới hạn vô cực: + Nếu biểu thức có dạng phân thức mà mẫu và tử đều chứa các lũy thừa của n, thì chia tử và mẫucho nk, với k là số mũ cao nhất. + Nếu biểu thức có chứa n dưới dấu căn, thì có thể nhân tử số và mẫu số với cùng một biểu thứcliên hợp. 10. Phương pháp tính tổng của cấp số nhân lùi vô hạn

admincd

Trả lời Hủy

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *

Bình luận *

Tên *

Email *

Trang web

Lưu tên của tôi, email, và trang web trong trình duyệt này cho lần bình luận kế tiếp của tôi.

• 
  

• Assign a menu in Theme Options > Menus

WooCommerce not Found

• 
  
  Newsletter