Download.vn Học tập Lớp 12
Bạn đang đọc: Một số bài toán phương trình logarit khác cơ số
Một số bài toán phương trình logarit khác cơ số Tài liệu ôn tập môn Toán lớp 12
Giới thiệu Tải về Bình luận
- 2
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Nhằm đem đến cho các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập môn Toán Download.vn xin giới thiệu tài liệu Một số bài toán phương trình logarit khác cơ số.
Để giải các dạng bài tập về phương trình logarit với cơ số khác nhau, nhiều học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về các phương trình cơ bản.Tài liệu này sẽ giới thiệu các phương pháp thường được áp dụng để giải dạng toán này. Bao gồm: Đổi cơ số; Đặt ẩn phụ để đưa về phương trình mũ; Biến đổi tương đương; Đánh giá hai vế. Hy vọng qua tài liệu này các bạn nắm vững được kiến thức giải nhanh các bài toán để đạt kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia. Mời các bạn cùng theo dõi.
Một số bài toán phương trình logarit khác cơ số
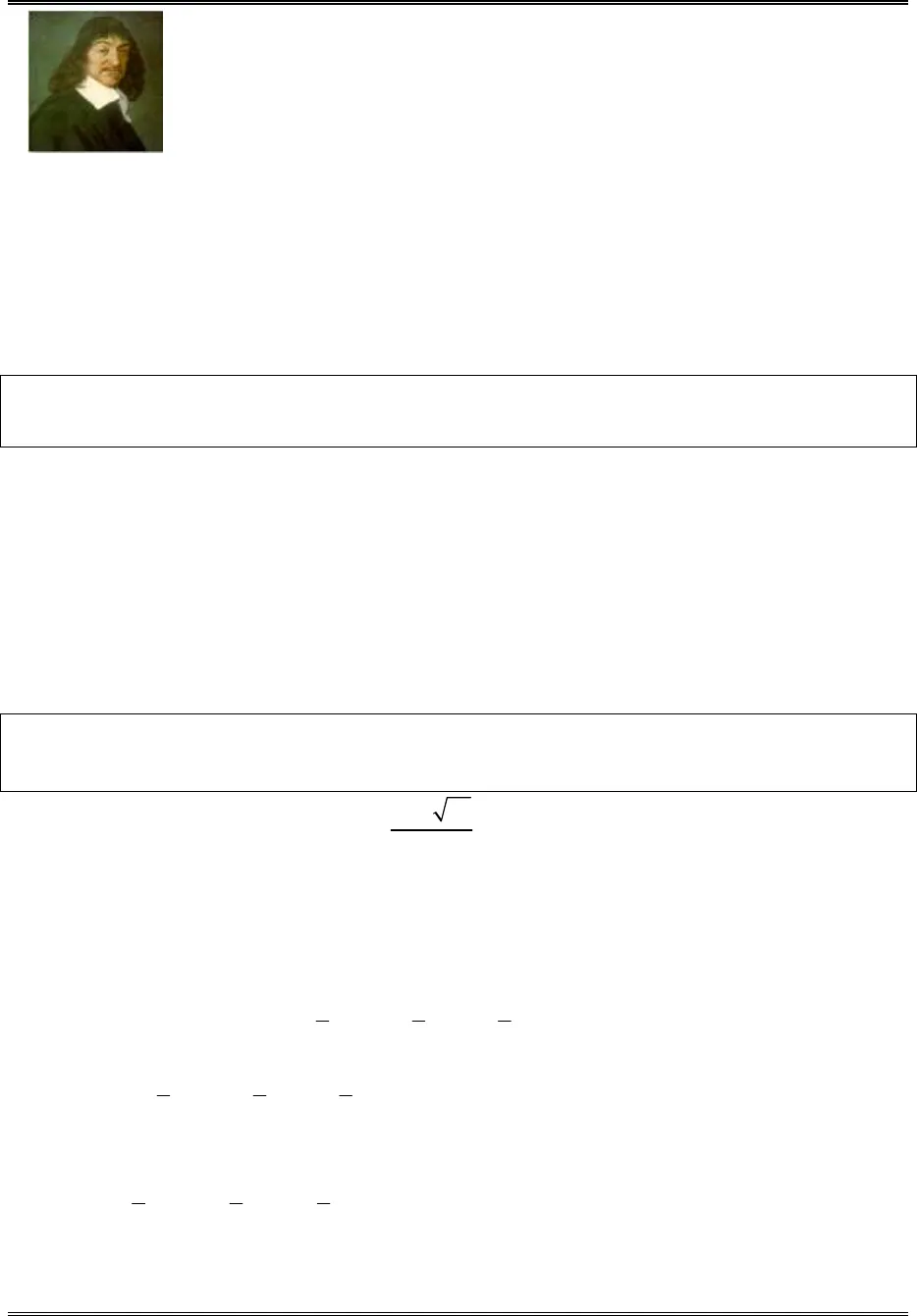Chuaån bò cho kyø thi Ñaïi hoïcPage 1VVVVài bài toán về phương trình logarit khác cơ số Huỳnh Đức Khánh – 0975.120.189Descartes Giải tích – ĐH Quy NhơnPhương trình logarit với cơ số khác nhau luôn là vấn đề gây khó dễ cho học sinh khi gặp phảitrong các đề thi. Học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa vềcác phương trình cơ bản. Tôi viết bài xin đóng góp vài bài mẫu về vấn đề này, nó được dùng các phươngpháp: Đổi cơ số, đặt ẩn phụ để đưa về phương trình mũ, biến đổi tương đương, đánh giá hai vế. Ví dụ 1. Giải phương trình: 2 3 4 20log x log x log x log x+ + = . Điều kiện:x 0>.Với điều kiện trên phương trình tương đương2 3 2 4 2 20 2log x log 2.log x log 2.log x log 2.log x+ + =()2 3 4 20log x 1 log 2 log 2 log 2 0⇔ + + − = 2log x 0⇔ =(do3 4 201 log 2 log 2 log 2 0+ + − ≠)x 1⇔ =(thỏa mãn).Vậy phương trình có nghiệmx 1=.Ví dụ 2. Giải phương trình: ()23 2log x 3x 13 log x− − =.Điều kiện:2x 3x 13 03 61xx 02 − − >+⇔ >>.Đặt:t2log x t x 2= ⇔ =.Phương trình trở thành:( )t t3log 4 3.2 13 t− − =t t t4 3.2 13 3⇔ − − =t t t3 1 21 13 34 4 4 ⇔ = + + . (*)Hàm sốt t t3 1 2y 13 34 4 4 = + + là tổng của các hàm nghịch biến nên y nghịch biến,hàmy 1=là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất.Ta có:3 3 33 1 21 13 34 4 4 = + + . Suy ra phương trình (*) có nghiệmt 3=.Với3t 3 x 2 8= ⇒ = =(thỏa mãn).Vậy phương trình có nghiệm duy nhấtx 8=.
Chuaån bò cho kyø thi Ñaïi hoïcPage 2Ví dụ 3. Giải phương trình: ()2 3log 1 x log x+ = . Điều kiện: x 0> . Đặt:t3log x t x 3= ⇔ = . Phương trình trở thành:( )t2log 1 3 t+ =t t1 3 2⇔ + =tt1 312 2 ⇔ + = . (*)Hàm sốtt1 3y2 2 = + là tổng của các hàm nghịch biến nên y nghịch biến, hàmy 1=là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất.Ta có:221 312 2 + = . Suy ra phương trình (*) có nghiệmt 2=.Với2t 2 x 3 9= ⇒ = =(thỏa mãn).Vậy phương trình có nghiệm duy nhấtx 9=.Ví dụ 4. Giải phương trình: ()()2 23 2log x 2x 1 log x 2x+ + = +. (1)Điều kiện:22x 2x 1 0 x 2x 0x 2x 0 + + > −⇔>+ >.Đặt:2u x 2x= +. Phương trình (1) trở thành:()3 2log u 1 log u+ =. (2) Xét phương trình (2). Ta đặt:t2log u t u 2= ⇔ =.Phương trình (2) trở thành:( )t3log 2 1 t+ =t t2 1 3⇔ + =t t2 113 3 ⇔ + = . (3)Hàm sốt t2 1y3 3 = + là tổng của các hàm nghịch biến nên y nghịch biến, hàmy 1=là hàm hằng. Do đó phương trình (3) có nghiệm duy nhất.Ta có:1 12 113 3 + = . Suy ra phương trình (3) có nghiệmt 1=.Với1 2x 1 3t 1 u 2 2 x 2x 2x 1 3= − −= ⇒ = = ⇒ + = ⇔= − +(thỏa mãn).Vậy phương trình có nghiệmx 1 3; x 1 3= − − = − +.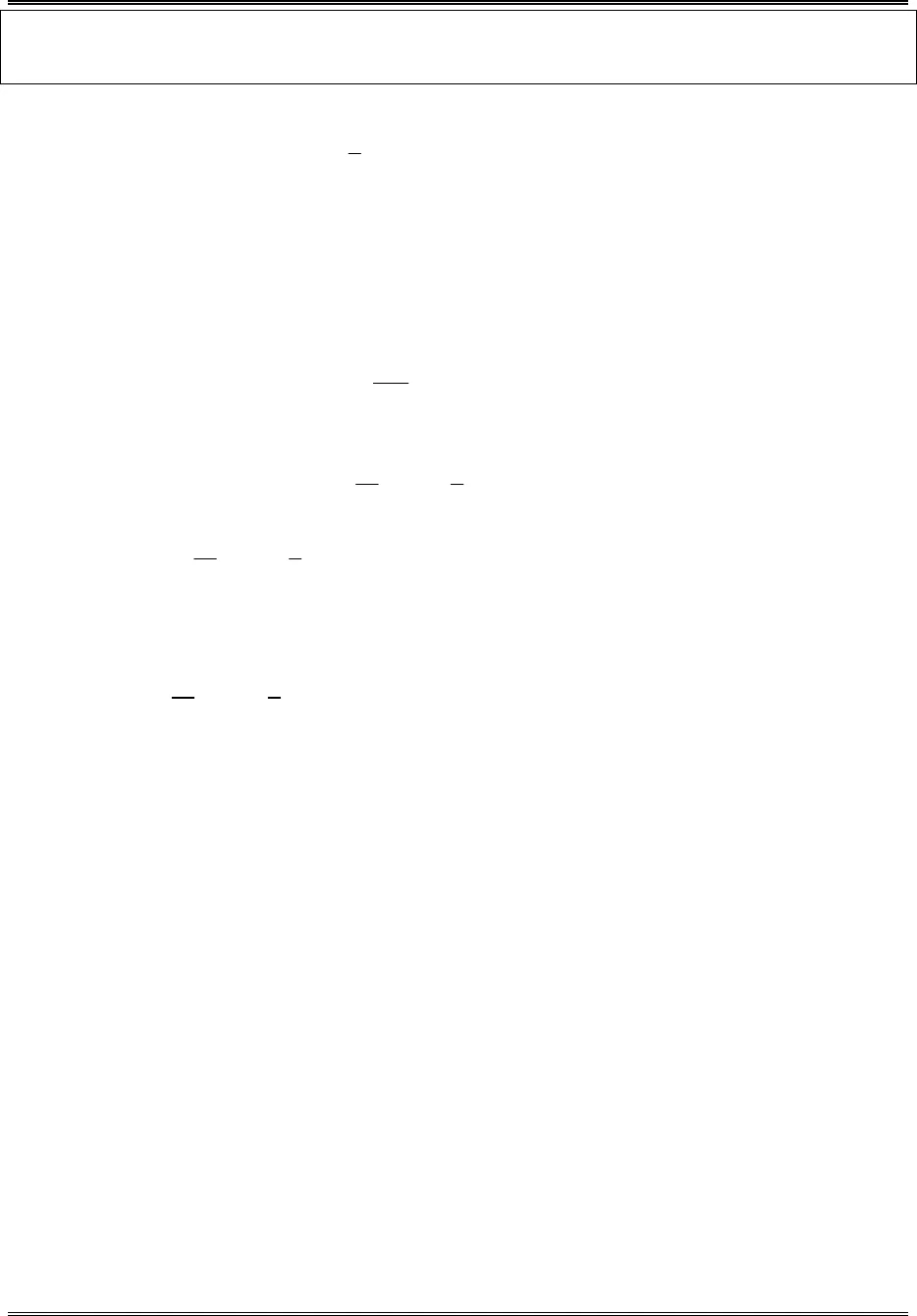
Chuaån bò cho kyø thi Ñaïi hoïcPage 3Ví dụ 5. Giải phương trình: ()()3 5log x 1 log 3x 1 4+ + + =.Điều kiện:x 1 01x3x 1 03+ >⇔ > −+ >.Đặt:()t3log x 1 t x 1 3+ = ⇔ + = , suy ra: t3x 1 3.3 2+ = −.Phương trình trở thành:( )t5t log 3.3 2 4+ − =( )t5log 3.3 2 4 t⇔ − = −t 4 t3.3 2 5−⇔ − =tt6253.3 25⇔ − =t t3.15 2.5 625⇔ − =t t1 13 625 215 3 ⇔ = + .Hàm sốt t1 1y 625 215 3 = + là tổng của các hàm nghịch biến nên y nghịch biến, hàmy 3=là hàm hằng. Do đó phương trình có nghiệm duy nhất.Ta có:2 21 13 625 215 3 = + . Suy ra phương trình có nghiệmt 2=.Với2t 2 x 1 3 x 8= ⇒ + = ⇔ =(thỏa mãn).Vậy phương trình có nghiệm duy nhấtx 8=.Cách khác: ● Kiểm trax 8=là nghiệm của phương trình.● Nếux 8>thì()()()()( ) ( )3 33 55 5log x 1 log 8 1 2log x 1 log 3x 1 4log 3x 1 log 3.8 1 2+ > + =⇒ + + + >+ > + =.● Nếux 8thì()()()()( ) ( )3 33 55 5log x 1 log 8 1 2log x 1 log 3x 1 4log 3x 1 log 3.8 1 2+ + =⇒ + + + + =.Vậy phương trình có nghiệm duy nhấtx 8=.