Download.vn Học tập Lớp 12
Bạn đang đọc: Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số Tài liệu luyện thi THPT Quốc gia 2019
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 cùng tham khảo.
Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số là tài liệu gồm 96 trang tuyển tập bài tập trắc nghiệm về cực trị của hàm số, nội dung gồm 4 phần: Biện luận nghiệm bằng đồ thị; Biến đổi đồ thị trị tuyệt đối; Tổng ôn; Phép tịnh tiến. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tại đây.
Phương pháp giải trắc nghiệm chuyên đề hàm số
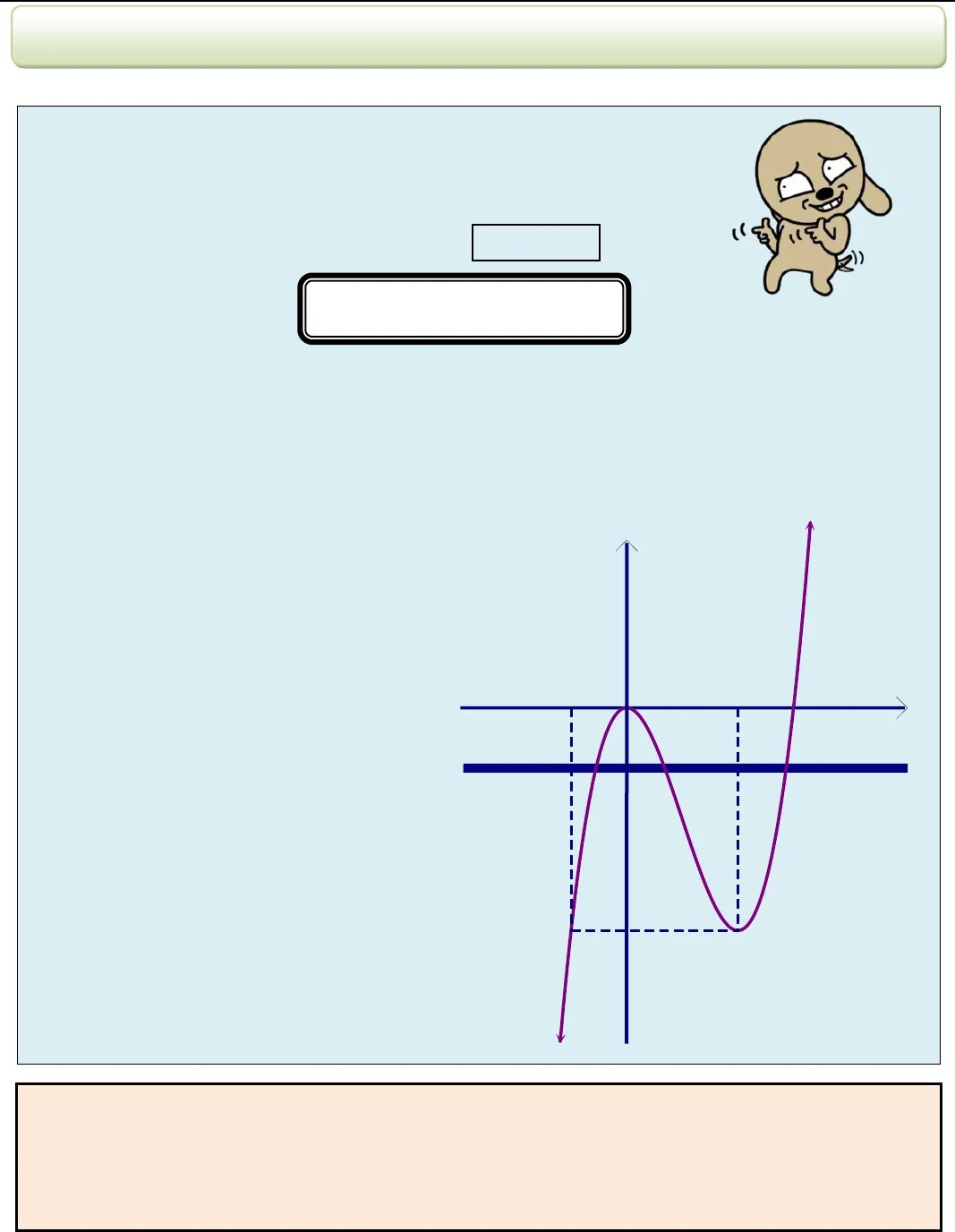 1Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 ◙ Lý Thuyết : Ta xét bài toán sau đây : Vẽ đồ thị (C) của hàm số()y f xsau đó biện luận theo tham số m số nghiệm của phương trình : ( ; m) 0hx (♥)☻ Ta đưa (♥) về dạng Trong đó()fmlà biểu thức theo m, không chứa xSố nghiệm của (♥) chính là số giao điểm của (C) và đường thẳng (D)()y f mmà ta nhìn thấy qua đồ thị ((D) ……………………….. Ox ) VD như hình bên, ta thấy (♥) có : ☻ 3 nghiệm khi …………………………………….. ☻ 2 nghiệm khi ………………….. hoặc ………………………….☻ 1 nghiệm khi ………………….. hoặc ………………………….Ví dụ 01 : Cho hàm số 3234y x x (có đồ thị là (C)) a/ Khảo sát và vẽ đồ thị hàm số. b/ Biện luận theomsố nghiệm của phương trình 3230x x m .PHẦN 8 : BIỆN LUẬN NGHIỆM BẰNG ĐỒ THỊ _ x _ , _ _ y _ = _ f _ ( _ m _ ) _ y _ -4 _ 3 _ 2 _ – 1 _ O
1Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 ◙ Lý Thuyết : Ta xét bài toán sau đây : Vẽ đồ thị (C) của hàm số()y f xsau đó biện luận theo tham số m số nghiệm của phương trình : ( ; m) 0hx (♥)☻ Ta đưa (♥) về dạng Trong đó()fmlà biểu thức theo m, không chứa xSố nghiệm của (♥) chính là số giao điểm của (C) và đường thẳng (D)()y f mmà ta nhìn thấy qua đồ thị ((D) ……………………….. Ox ) VD như hình bên, ta thấy (♥) có : ☻ 3 nghiệm khi …………………………………….. ☻ 2 nghiệm khi ………………….. hoặc ………………………….☻ 1 nghiệm khi ………………….. hoặc ………………………….Ví dụ 01 : Cho hàm số 3234y x x (có đồ thị là (C)) a/ Khảo sát và vẽ đồ thị hàm số. b/ Biện luận theomsố nghiệm của phương trình 3230x x m .PHẦN 8 : BIỆN LUẬN NGHIỆM BẰNG ĐỒ THỊ _ x _ , _ _ y _ = _ f _ ( _ m _ ) _ y _ -4 _ 3 _ 2 _ – 1 _ O 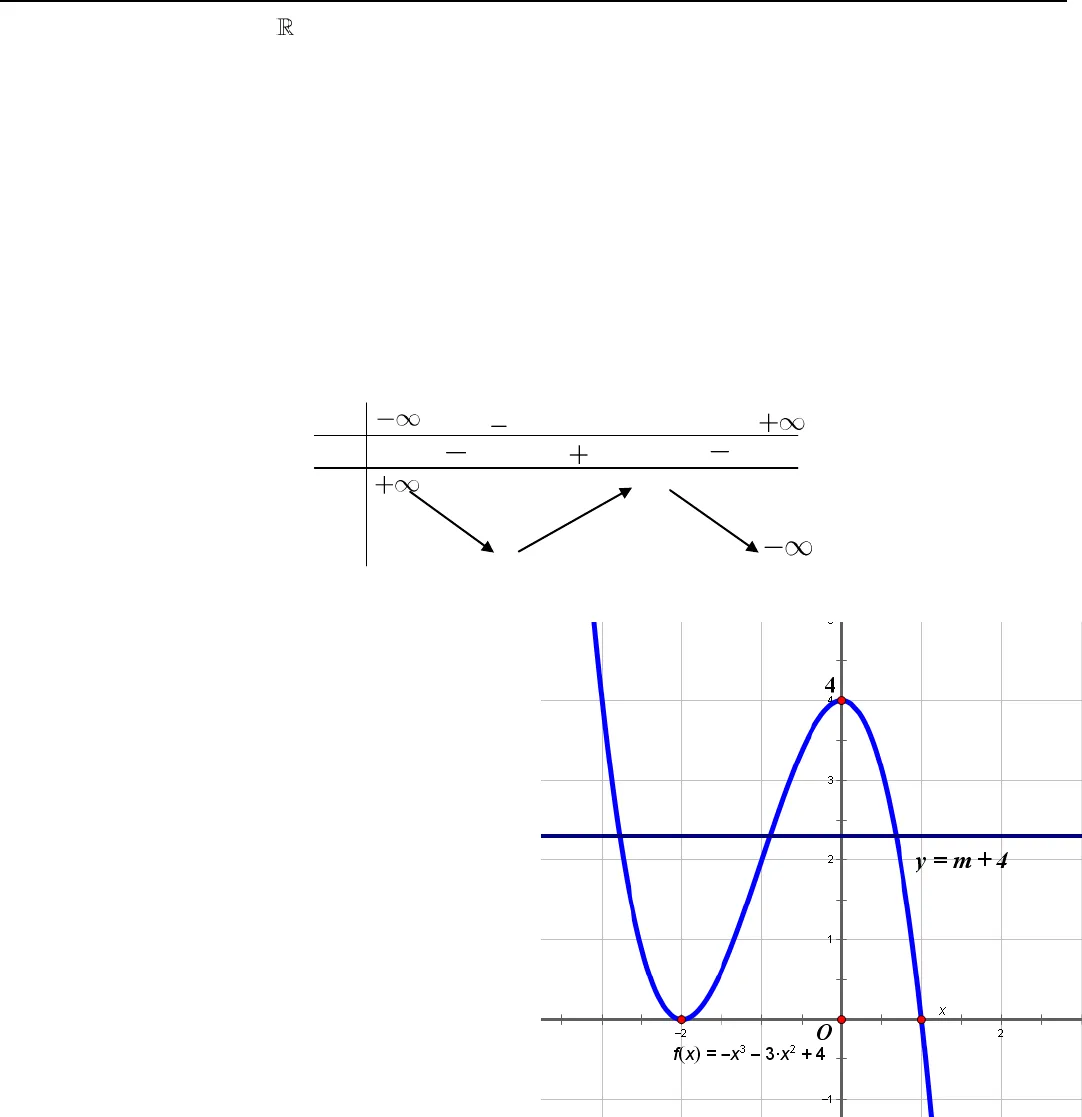 2Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 a/ ► Tập xác định D .► Đạo hàm 2′ 3 6 3 2y x x x x ;0’02xyx.► Hàm số đồng biến trên khoảng 2;0;nghịch biến trên các khoảng ;2 và 0;.► Hàm số đạt cực đại tại 0x ,CD4y ; đạt cực tiểu tại 2x ,CT0y .► Giới hạn tại vô cực limxy ; vàlimxy .► Bảng biến thiên ► Đồ thị hàm số đi qua các điểm 3;4, 1;0.b/ Ta có3230x x m 323 4 4 *x x m . Phương trình *là phương trình hoành độgiao điểm của đồ thị và đường thẳng 4ym.Do đó số nghiệm của phương trình *là số giao điểm của đồ thị và đường thẳngd:4ym. (d cùng phương Ox)Dựa vào đồ thị, ta có♥ Với 4 4 04 0 4mmmm : Phương trình códuy nhất 1nghiệm. ♥ Với 4 4 04 0 4mmmm : Phương trình có 2nghiệm. ♥ Với 0 4 4 4 0mm : Phương trình có 3nghiệm. yx’y240000
2Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 a/ ► Tập xác định D .► Đạo hàm 2′ 3 6 3 2y x x x x ;0’02xyx.► Hàm số đồng biến trên khoảng 2;0;nghịch biến trên các khoảng ;2 và 0;.► Hàm số đạt cực đại tại 0x ,CD4y ; đạt cực tiểu tại 2x ,CT0y .► Giới hạn tại vô cực limxy ; vàlimxy .► Bảng biến thiên ► Đồ thị hàm số đi qua các điểm 3;4, 1;0.b/ Ta có3230x x m 323 4 4 *x x m . Phương trình *là phương trình hoành độgiao điểm của đồ thị và đường thẳng 4ym.Do đó số nghiệm của phương trình *là số giao điểm của đồ thị và đường thẳngd:4ym. (d cùng phương Ox)Dựa vào đồ thị, ta có♥ Với 4 4 04 0 4mmmm : Phương trình códuy nhất 1nghiệm. ♥ Với 4 4 04 0 4mmmm : Phương trình có 2nghiệm. ♥ Với 0 4 4 4 0mm : Phương trình có 3nghiệm. yx’y240000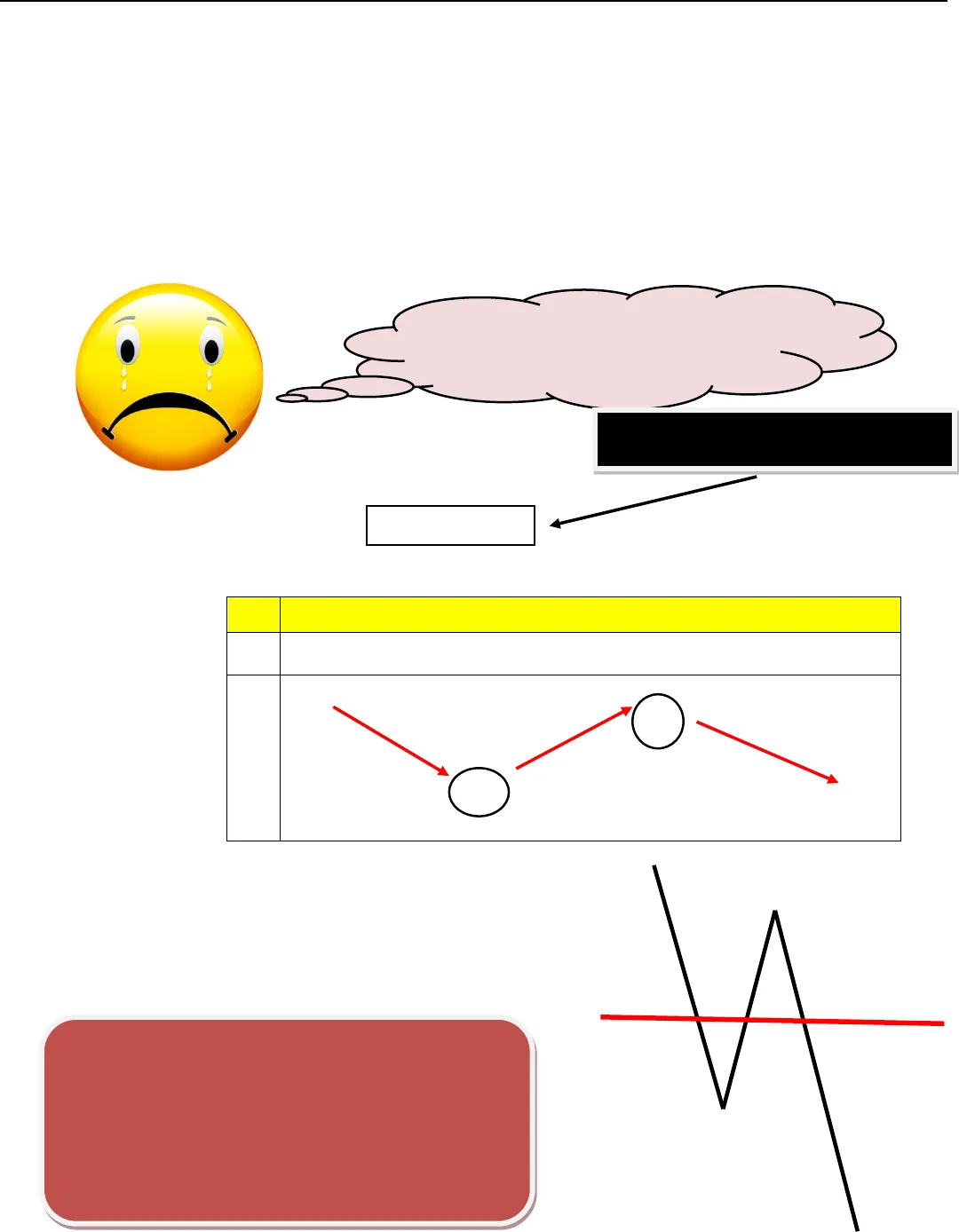 3Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 0-4-∞+∞ m☻Toán nếu trắc nghiệm thì đề sẽ bắt chúng ta “suy luận và hiểu” nhiều hơn là phương pháp “Casio thần chưởng” ☻Vậy phải làm sao ??? ☻Thật ra thì “bảng biến thiên đã nói lên tất cả”rồi Chúng ta bắt tay vào làm !!! Ở đây thầy không dùng bảng biến thiên cũ (nếu dùng vẫn được) để cho các em biết là đưa về hàm nào cũng được ☺ Phương trình 3230x x m ta viết lại 323m x x Lập BBT đi “phác thảo” đồ thị Từ đồ thị “phác thảo” này ta thấy rõ ràngở đây thầy ví dụ có 3 nghiệm !!!thì m chạy từ – 4 đến 0 x20’y00y042 con số đáng yêu !!! (biện luận ko cần vẽ đồ thị) Đây không phải là công thức giải nhanh – chỉ là hướng tư duy giúp giải bài toán nhanh hơn cho trắc nghiệm !! Vẽ đồ thị mất 15 phút rồiNhìn hàm g(x) này nè !!!
3Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – BIỆN LUẬN 2017 0-4-∞+∞ m☻Toán nếu trắc nghiệm thì đề sẽ bắt chúng ta “suy luận và hiểu” nhiều hơn là phương pháp “Casio thần chưởng” ☻Vậy phải làm sao ??? ☻Thật ra thì “bảng biến thiên đã nói lên tất cả”rồi Chúng ta bắt tay vào làm !!! Ở đây thầy không dùng bảng biến thiên cũ (nếu dùng vẫn được) để cho các em biết là đưa về hàm nào cũng được ☺ Phương trình 3230x x m ta viết lại 323m x x Lập BBT đi “phác thảo” đồ thị Từ đồ thị “phác thảo” này ta thấy rõ ràngở đây thầy ví dụ có 3 nghiệm !!!thì m chạy từ – 4 đến 0 x20’y00y042 con số đáng yêu !!! (biện luận ko cần vẽ đồ thị) Đây không phải là công thức giải nhanh – chỉ là hướng tư duy giúp giải bài toán nhanh hơn cho trắc nghiệm !! Vẽ đồ thị mất 15 phút rồiNhìn hàm g(x) này nè !!! 
