Download.vn Học tập Lớp 7 Toán 7 Kết nối tri thức

Bạn đang đọc: Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực

Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực Ôn tập môn Toán lớp 7 chương 1

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Với mong muốn đem đến cho các bạn học sinh lớp 7 có thêm nhiều tài liệu học tập môn Toán, Download.vn giới thiệu tài liệu Phương pháp giải các dạng toán chuyên đề số hữu tỉ, số thực.

Đây là tài liệu cực kì hữu ích, gồm 42 trang tổng hợp lý thuyết trong sách giáo khoa, phân dạng và hướng dẫn giải các dạng toán chuyên đề số hữu tỉ – số thực trong chương trình Đại số 7 chương 1. Hi vọng với tài liệu này các bạn có thêm nhiều tư liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi học kì 1 sắp tới. Ngoài ra các bạn tham khảo thêm tài liệu Tổng hợp bài tập Chương I môn Toán lớp 7. Mời các bạn cùng theo dõi và tải tài liệu tại đây.

Phương pháp giải dạng toán chuyên đề số hữu tỉ, số thực

CHUYÊN ĐỀ SỐ HỮU TỈ – SỐ THỰC ĐẠI SỐ 7§1. TẬP HỢP QCÁC SỐ HỮU TỈA. TÓM TẮT LÝ THUYẾT1. Số hữu tỉ là số viết được dưới dạng phân sốabvới, , ab b02. Ta có thể biểu diễn mọi số hữu tỉ trên trục số. Trên chục số, điểm biểu diễn số hữu tỉđược gọi là điểmx3. Với hai số hữu tỉ bất kỳ,xyta luôn có hoặcxyhoặcxyhoặcxy. Ta có thể sosánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.• Nếuxythì trên trục số, điểmxở bên trái điểm;y• Sốhữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;• Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm;• Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.B. CÁC DẠNG TOÁNDạng 1. SỬ DỤNG CÁC KÍ HIỆU, , , , , . Phương pháp giải.Cần nắm vững ý nghĩa của từng ký hiệu: • Kí hiệuđọc là “phần tử của” hoặc “thuộc”.• Kí hiệuđọc là “không phải là phần tử của” hoặc “khồng thuộc”.• Kí hiệuđọc là “là tập hợp con của”.• Kí hiệuchỉ tập hợp các số tự nhiên.• Kí hiệuchỉ tập hợp các số nguyên.• Kí hiệuchỉ tập hợp các số hữu tỉ.Ví dụ 1. (Bài 1 tr.7 SGK)Điền ký hiệu  , , thích hợp vào ô trống:-3 ; -3 ; -323; 23; Giải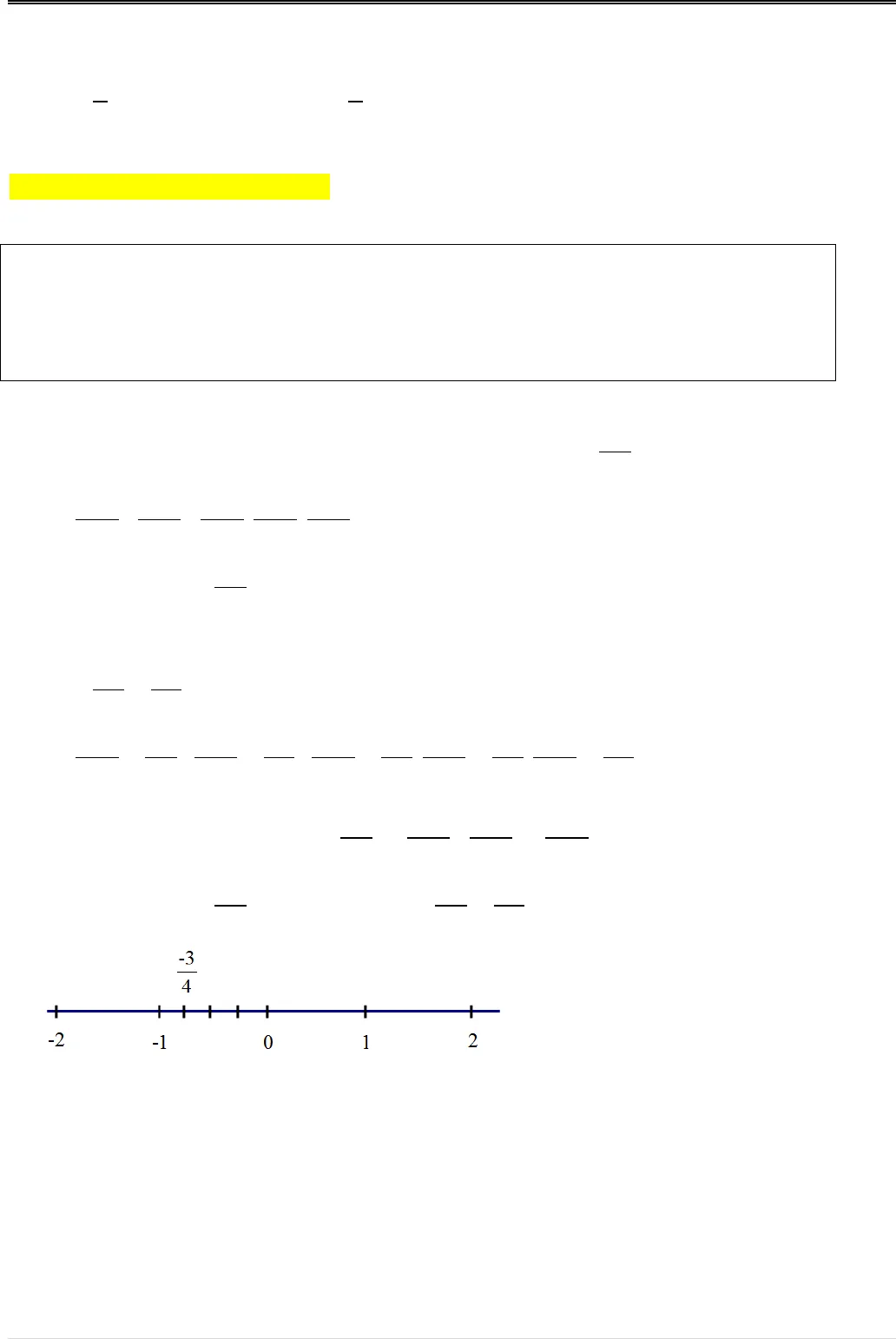-3; -3; -323; 23;Dạng 2. BIỂU DIỄN SỐ HỮU TỈPhương pháp giải. •Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản.• Khi biểu diến số hữu tỉ trên trục số, ta thường viết số đó dưới dạng phân số tối giản cómẫu dương. Khi đó mẫu cửa phân số cho biết đoạn thẳng đơn vị cần được chia thành baonhiêu phần bằng nhau.Ví dụ 2. (Bài 2 tr.7 SGK)a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ34:, , , , ?  12 15 24 20 2715 20 32 28 36b) Biểu diễn số hữu tỉ34trên trục số.Giảia) Ta có.3344Rút gọn các phân số đã cho ta được:; ; ; ; .   12 4 15 3 24 3 20 5 27 315 5 20 4 32 4 28 7 36 4Vậy các phân số biểu diễn số hữu tỉ34là:;15 2420 32và2736b) Biểu diễn số hữu tỉ34trên trục số: Ta viết3344và biểu diễn trên trục số như sau: 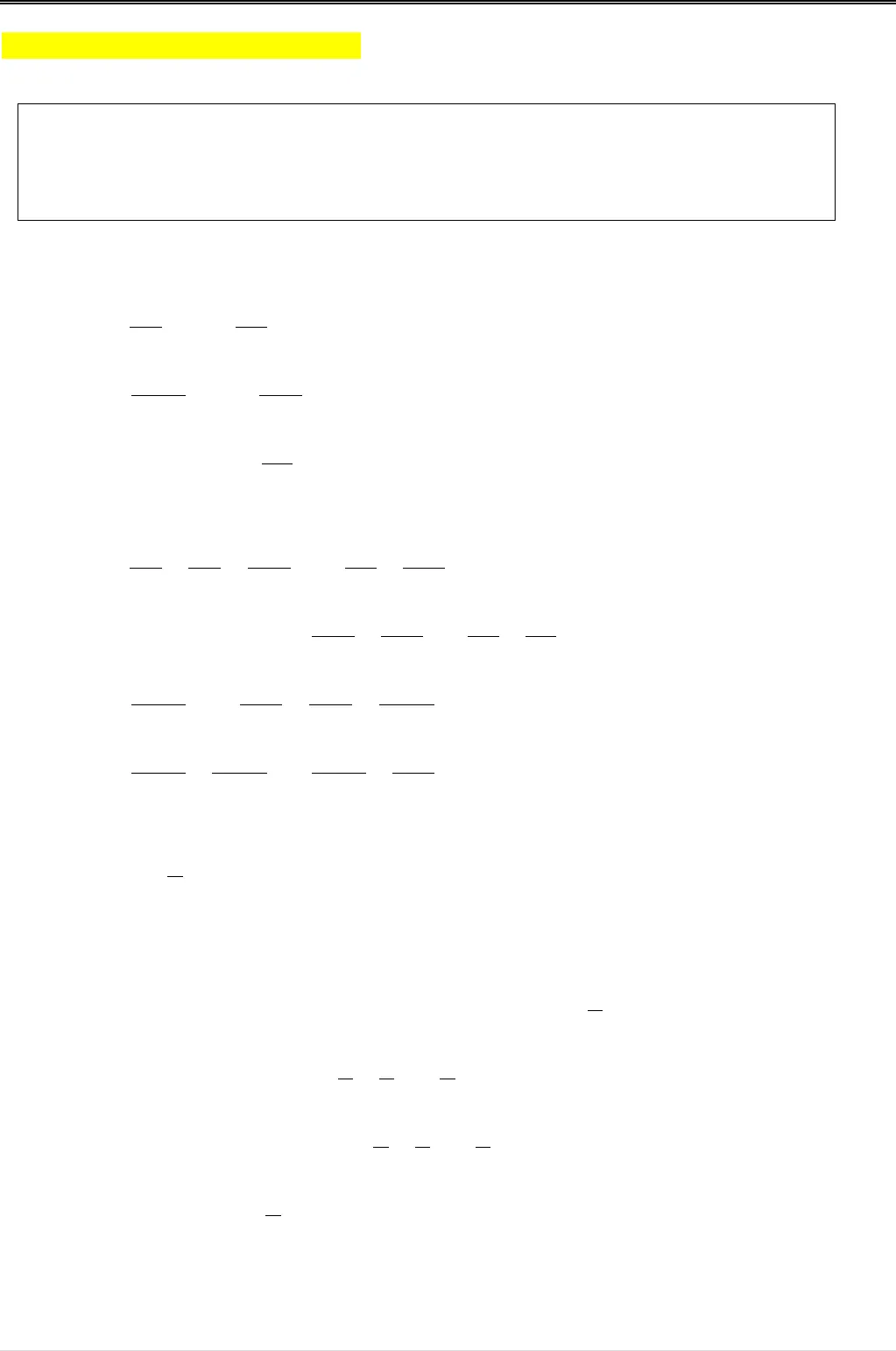Dạng 3. SO SÁNH CÁC SỐ HỮU TỈPhương pháp giải. • Viết các số hữu tỉ dưới dạng phân số có cùng một mẫu dương;• So sánh các tử, phân số nào tử nhỏ hơn thì phân số đó nhỏ hơn.• Có thể sử dụng tính chất sau để so sánh: Nếu, , abc vàabthì.acbcVí dụ 3. (Bài 3 tr.8 SGK)So sánh các số hữu tỉ:a)x 27và;y311b)x213300và;y 1825c),x 0 75và;y34Giải a); .xy  2 2 22 3 217 7 77 11 77 22 21và77 0nên22 2177 77hay( ).xy237 11b); .xy  213 18 18 216300 25 25 300Ta có:213 216300 300hay( ).xy213 18300 25Ví dụ 4. (Bài 4 tr.8 SGK)So sánh số hữu tỉ( , , )aab bb0với số 0 khi,abcùng dấu và khi,abkhác dấu.Giải Nhờ tính chất cơ bản của phân số, ta luôn có thể viết một phân số có mẫu âm thành một phân số bằng nó và có mẫu dương. Vì vậy, ta chỉ cần nhận xét số hữu tỉ ( , , ).aab bb0Nếu cùng dấu thì ta có.a  0Do đóabb0hay.ab 0Nếu,abkhác dấu thì ta có.a  0Do đóabb0hay.ab 0Nhận xét: Số hữu tỉ ( , , )aab bb0là số dương nếu ,abcùng dấu, là số âm nếu,abkhác dấu, bằng 0 nếu.a  0Ví dụ 5. (Bài 5 tr.8 SGK)