Download.vn Học tập Lớp 7 Toán 7 Kết nối tri thức
Bạn đang đọc: Phương pháp giải các dạng toán chuyên đề tam giác
Phương pháp giải các dạng toán chuyên đề tam giác Tài liệu ôn tập lớp 7 môn Toán
Giới thiệu Tải về Bình luận
- 10
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Mời quý thầy cô cùng các bạn học sinh lớp 7 tham khảo tài liệu Phương pháp giải các dạng toán chuyên đề tam giác được Download.vn đăng tải trong bài viết dưới đây.
Tài liệu bao gồm 48 trang, tổng hợp lý thuyết SGK, phân dạng và hướng dẫn giải các dạng toán chuyên đề tam giác trong chương trình Hình học lớp 7. Nội dung tài liệu bao gồm phương pháp giải các dạng toán chuyên đề tam giác như:
- Tổng ba góc của một tam giác.
- Hai tam giác bằng nhau.
- Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh.
- Trường hợp bằng nhau thứ hai của tam giác cạnh – góc – cạnh.
- Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc.
- Tam giác cân
- Định lý Py-ta-go
- Các trường hợp bằng nhau của tam giác vuông
Phương pháp giải các dạng toán chuyên đề tam giác.
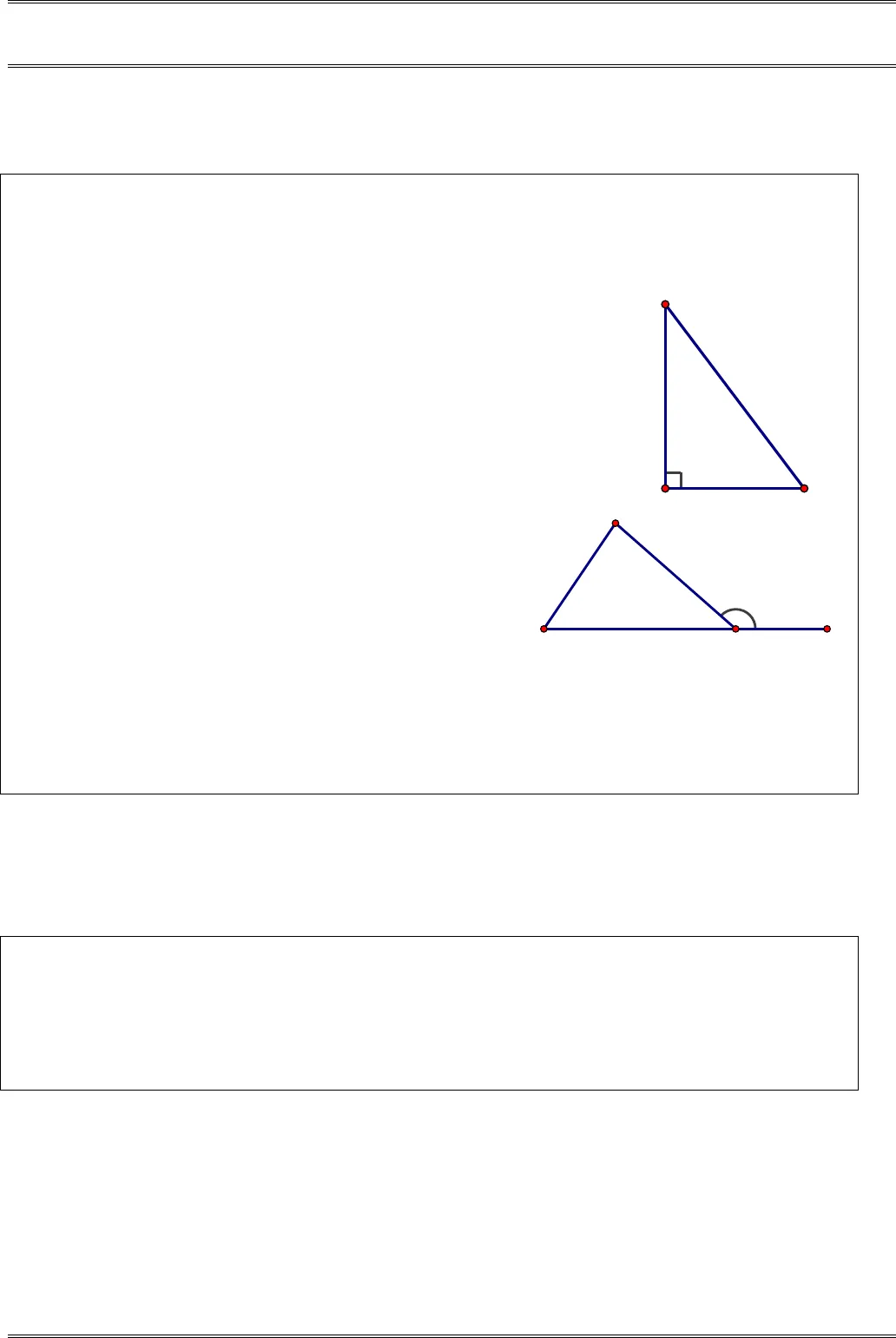§ 8. TỔNG BA GÓC CỦA MỘT TAM GIÁCA. TÓM TẮT LÝ THUYẾT1. Tổng ba góc của một tam giác.Tổng ba góc của một tam giác bằng180 .° 180ABC A B C∆ ⇒++= °2. Áp dụng vào tam giác vuônga) Định nghĩa: Tam giác vuông là tam giác có một góc vuông.b) Tính chất: Trong tam giác vuông, hai góc nhọn phụ nhau9090ABCBCA∆⇒+=°= °3. Góc ngoài củatam giáca) Định nghĩa: Góc ngoài của tam giác là góc kềbù với một góc của tam giác. b) Tính chất:• Mỗi góc ngoài của một tam giác bằng tổng haigóc trong không kề với nó. .ACD A B= +• Góc ngoài của tam giác lớn hơn mỗi góc trongkhông kề với nó.,ACD A>.ACD B>B. CÁC DẠNG TOÁNDạng 1. TÍNH SỐ ĐO GÓC CỦA MỘT TAM GIÁC Phương pháp giải. • Lập các đẳng thức thể hiện:– Tổng ba góc của tam giác bằng180 .°– Trong tam giác vuông, hai góc nhọn phụ nhau.- Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.• Sau đó tính số đo của góc phải tìm.Ví dụ 1. (Bài 1 tr.108 SGK) Cho tam giácABCcó80 ,B = °30 .C = °Tia phân giác của góc AcắtBCởD. Tính,ADC.ADBHướng dẫn. ACBBDAC-180– CHUYÊN ĐỀ TAM GIÁC
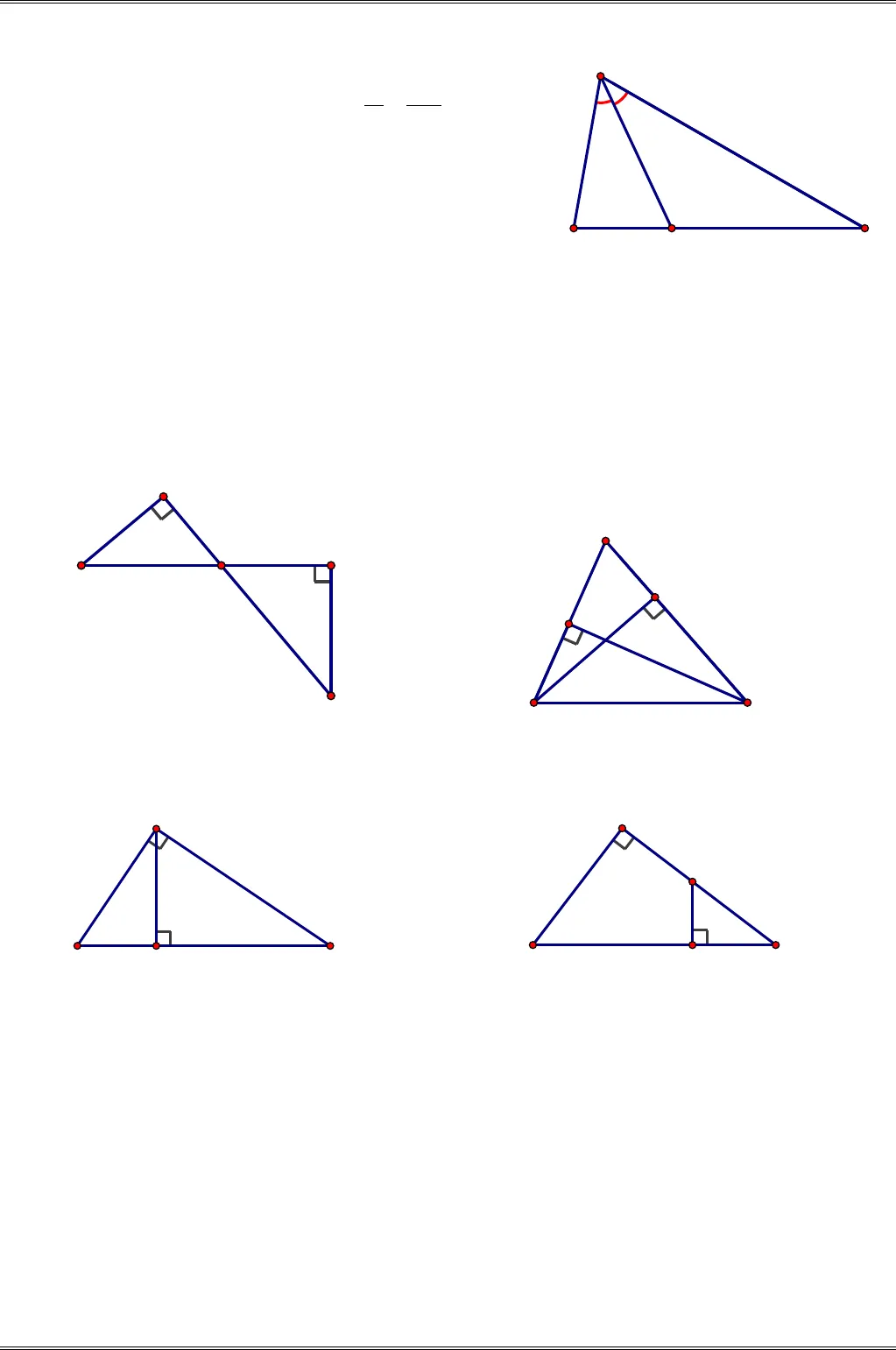:ABC∆ 180ABC++= °80 30 180A⇒ + °+ °= °70A⇒=°Do đó 127035 .22AAA°= = = = °Góc ngoài1ADC B A= +80 35 115= °+ °= °(góc ngoài của ABD∆). Suy ra 180 115 65 .ADB = °− °= °Ví dụ 2. (Bài 6 tr.109 SGK) Tìm số đo xở các hình55,56,57,58(SGK)Hình 55(SGK) Hình 56 (SGK)Hình 57 (SGK) Hình 58 (SGK) Giải.a)( ) 1290 40 .AI BI AB x+ = + = ° ⇒ = ⇒ °=b)( )90 25 .ABD A ACE A ABD ACE x+= +==°⇒ = ⇒= °c)119060 .90IMP MIMP N xNM+=°⇒ = ⇒= °+=°x21IBAKH25°xDABCEx60°1DBCAx55°BAEHK2130°80°DABC-181– 
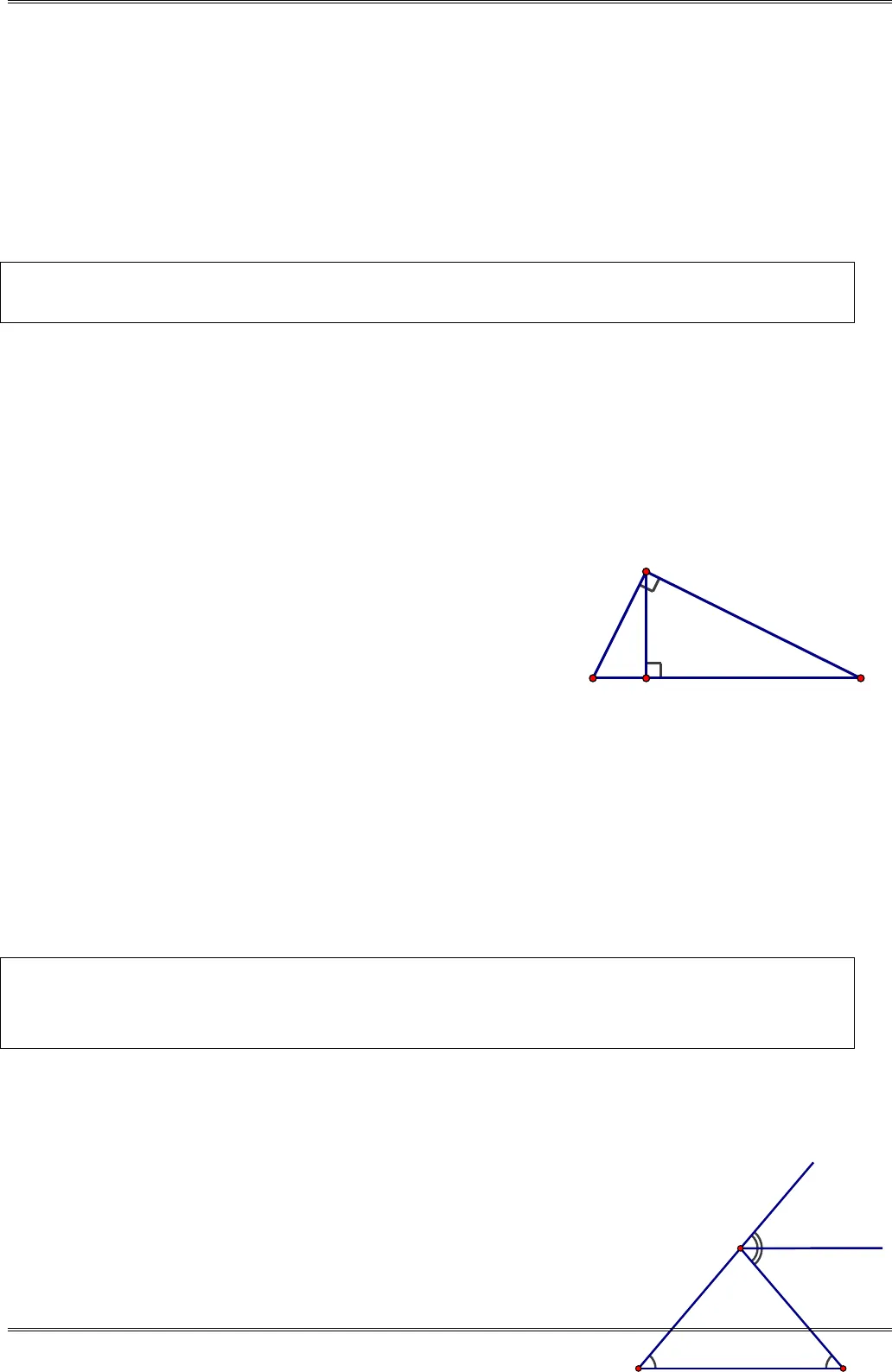d) 90 90 90 55 35 .AE E A+ = °⇒ = °− = °− °= °90 35 125 .x BKE E= + = °+ °= °Dạng 2. NHẬN BIẾT MỘT TAM GIÁC VUÔNG, TÌM CÁC GÓC BẰNG NHAU TRONG HÌNH VẼ CÓ TAM GIÁC VUÔNG. Phương pháp giải. Để nhận biết tam giác vuông, ta chứng minh tam giác đó có một góc bằng 90 .°Trong hình vẽ có tam giác vuông, cần chú ý rằng hai góc nhọn của tam giác vuông phụ nhau.Ví dụ 3. (Bài 7 tr.109 SGK) Cho tam giácABCvuông tạiA. KẻAHvuông góc vớiBC( )H BC∈a)Tìm các cặp góc phụ nhau trong hình vẽ.b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.Hướng dẫn. a)Các cặp góc phụ nhau: 1Avà2,ABvà,CBvà1,ACvà2.Ab) Các cặp góc nhọn bằng nhau:1CA=(cùng phụ với2A)2BA=(cùng phụ với1A).Dạng 3. CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG BẰNG CÁCH CHỨNG MINH HAI GÓC BẰNG NHAUPhương pháp giải. Chứng minh hai góc bằng nhau bằng cách chứng tỏ chúng cùng bằng, cùng phụ, cùng bù với một góc thứ ba (hoặc với hai góc bằng nhau). Từ chứng minh hai góc bằng nhau, ta chứngminh được hai đường thẳng song song. Ví dụ 4. (Bài 8 tr.109 SGK) Cho tam giácABCcó40 .BC= = °GọiAxlà tia phân giác của góc ngoài ở đỉnh.AHãy chứng tỏ rằng // .Ax BCHướng dẫn. 40 40 80 ,CAD B C= + = °+ °= °21HBCA21xDBCA-182– 