Download.vn Học tập Lớp 12

Bạn đang đọc: Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp

Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Với mong muốn đem đến cho các bạn có thêm nhiều tài liệu học tập, giải nhanh toán học lớp 12 Downoad.com.vn giới thiệu tài liệu Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp.

Phương pháp giải nhanh bài toán mặt cầu ngoại tiếp hình chóp là tài liệu hữu ích, với các công thức giải nhanh kèm theo ví dụ minh họa và 27 bài toán trắc nghiệm áp dụng. Hy vọng với tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới. Mời các bạn cùng tham khảo trong bài viết dưới đây.

Phương pháp giải nhanh mặt cầu ngoại tiếp hình chóp

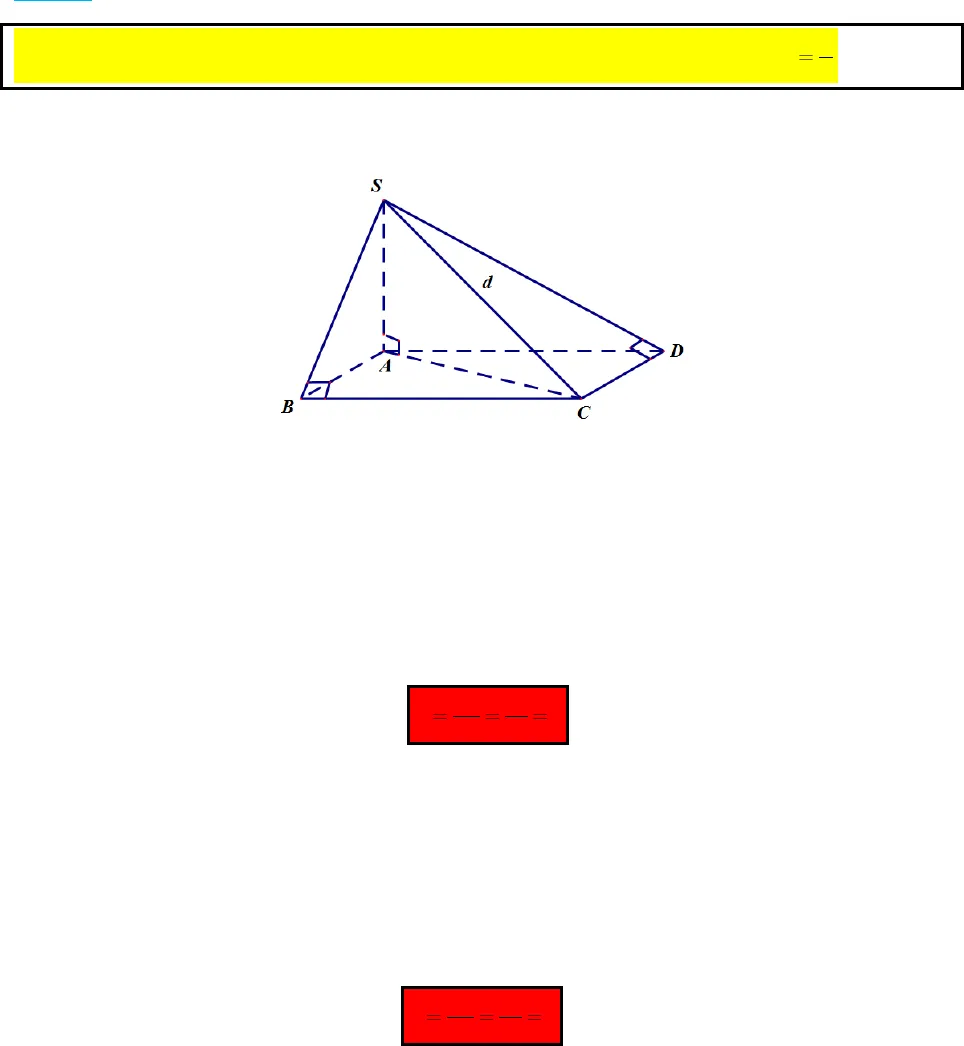GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : Trắc Nghiệm ToánPP tính nhanh bán kính mặt cầu ngoại tiếp các loạiLoại 1 : Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông. Gọi d là độ dài đoạn thẳng trên thì ta có bán kính mặt cầu ngoại tiếp là:2dRVí dụ : Cho hình chóp SABC có tam giác ABC vuông tại B , SA vuông góc với mặt phẳng (ABC) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên Giải : Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B từ đó hình chóp này loại 1 nên222SC aRaVí dụ : Cho hình chóp SABCD có đáy ABCD là hình vuông , SA vuông góc với mặt phẳng (ABCD) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên Giải : Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B và giác SDC vuông tại Dtừ đó hình chóp này loại 1 nên :222SC aRaLoại 2 : Hình chóp đều 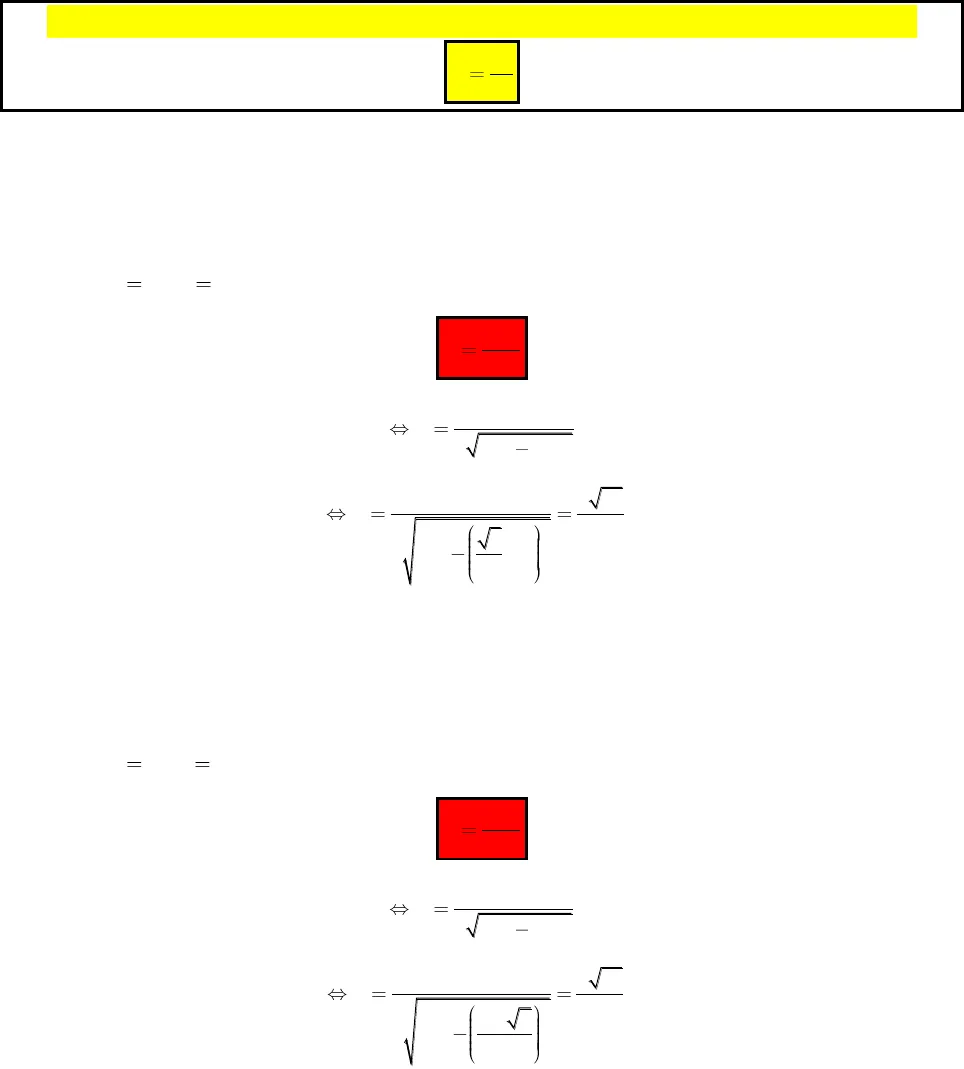GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : Trắc Nghiệm ToánGọi h là độ cao hình chóp và k là chiều dài cạnh bên thì ta có bán kính mặt cầu là :22kRhVí dụ : Cho hình chóp tam giác đều S.ABC , có AB=a và cạnh bên SA=2a , tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trênGiải : gọi G là trọng tâm tam giác thì ta có SG vuông góc với mặt phẳng (ABC) Thế thì ,SG hSA knên R mặt cầu : 22SARSG2222SARS AGA2222 3311323SARaSA ABVí dụ: Cho hình chóp tứ giác đều S.ABCD , có AB=a và cạnh bên SA=2a , tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trênGiải : gọi O là tâm hình vuông ABCD thì ta có SO vuông góc với mặt phẳng (ABCD) Thế thì ,SO hSA knên R mặt cầu :22SARSO2222SARS AOA2222 147222SARaABSALoại 3 : Hình chóp có cạnh bên vuông góc với đáy 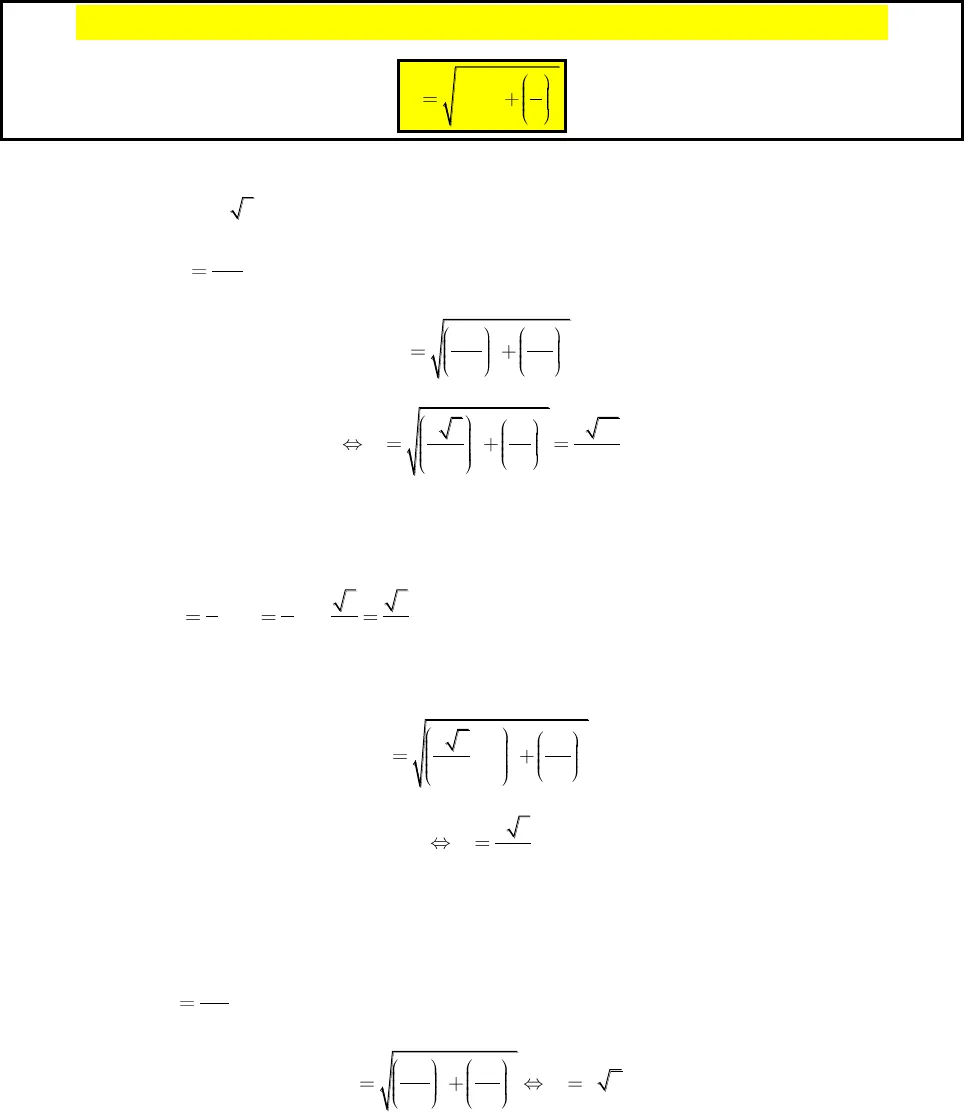GV : Hoàng Trọng Tấn , Tân Phú , TPHCM Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : Trắc Nghiệm ToánGọi h là chiều cao hình chóp vàdRlà bán kính của đáy thì bán kính mặt cầu :222dhRRVí dụ : cho hình chóp SABCD có cạnh SA vuông góc với đáy , ABCD là hình chữ nhật có đường chéo dài 5a, SA=2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCDGiải : Ta có : 2dayACRvà SA=hÁp dụng công thức ta có :2222SAACR225 21222aaaRaVí dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác đều cạnh = a , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCDGiải : Ta có 2 2 3 3.3 3 2 3dayR AM AB ABvà SA=hÁp dụng công thức ta có :222326SAR AB33aRVí dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác vuông tại A và BC=2a , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCDGiải : Ta có 2dayBCRvà SA=h .Áp dụng công thức ta có :22222SABCR R aVí dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam giác cân tại A và AB=a và góc A =120 độ , SA dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABC