Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Phương pháp giải phương trình lượng giác

Phương pháp giải phương trình lượng giác Tài liệu ôn tập môn Toán lớp 11

Giới thiệu Tải về Bình luận

• 7

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Với mong muốn bổ trợ thêm kiến thức và nâng cao trình độ nhận định bài giải Phương trình Lượng giác, Download.vn giới thiệu tài liệu Phương pháp giải phương trình lượng giác.

Đây là tài liệu vô cùng hữu ích đối với các em học sinh lớp 11, tài liệu gồm 49 trang tổng hợp toàn bộ các phương pháp giải kèm theo các bài tập giải phương trình lượng giác có đáp án chi tiết kèm theo. Mời các bạn cùng tham khảo và tải tài liệu tại đây.

Phương pháp giải phương trình lượng giác

ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 Trường THPT Nguyễn Hữu Tiến – Duy Tiên – Hà Nam 1I. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN 2 22 22 2sin 1 cossin cos 1cos 1 sinx xx xx x     2 22 21 11 tan tan 1cos cosx xx x     2 22 21 11 cot cot 1sin sinx xx x     1tan .cot 1 cottanx x xx   4 4 2 26 6 2 2sin cos 1 2 sin cos ;sin cos 1 3 sin cosx x x xx x x x     3 33 3sin cos (sin cos )(1 sin cos )sin cos (sin cos )(1 sin cos )x x x x x xx x x x x x      II. DẤU CỦA CÁC HÀM SỐ LƯỢNG GIÁC Góc I Góc II Góc III Góc IVsinxcosxtanxcotxIII. MỐI QUAN HỆ CỦA CÁC CUNG LƯỢNG GIÁC ĐẶC BIỆT Hai cung đối nhau cos( ) cosx x  sin( ) sinx x   tan( ) tanx x   cot( ) cotx x   Hai cung bù nhau sin( ) sinx x  cos( ) cosx x   tan( ) tanx x   cot( ) cotx x   Hai cung phụ nhau sin( ) cos2x x  cos( ) sin2x x  tan( ) cot2x x  cot( ) tan2x x  Hai cung hơn nhau sin( ) sinx x   cos( ) cosx x   tan( ) tanx x  cot( ) cotx x  Hai cung hơn nhau 2CÔNG THỨC LƯỢNG GIÁC CẦN NẮM VỮNGThS. 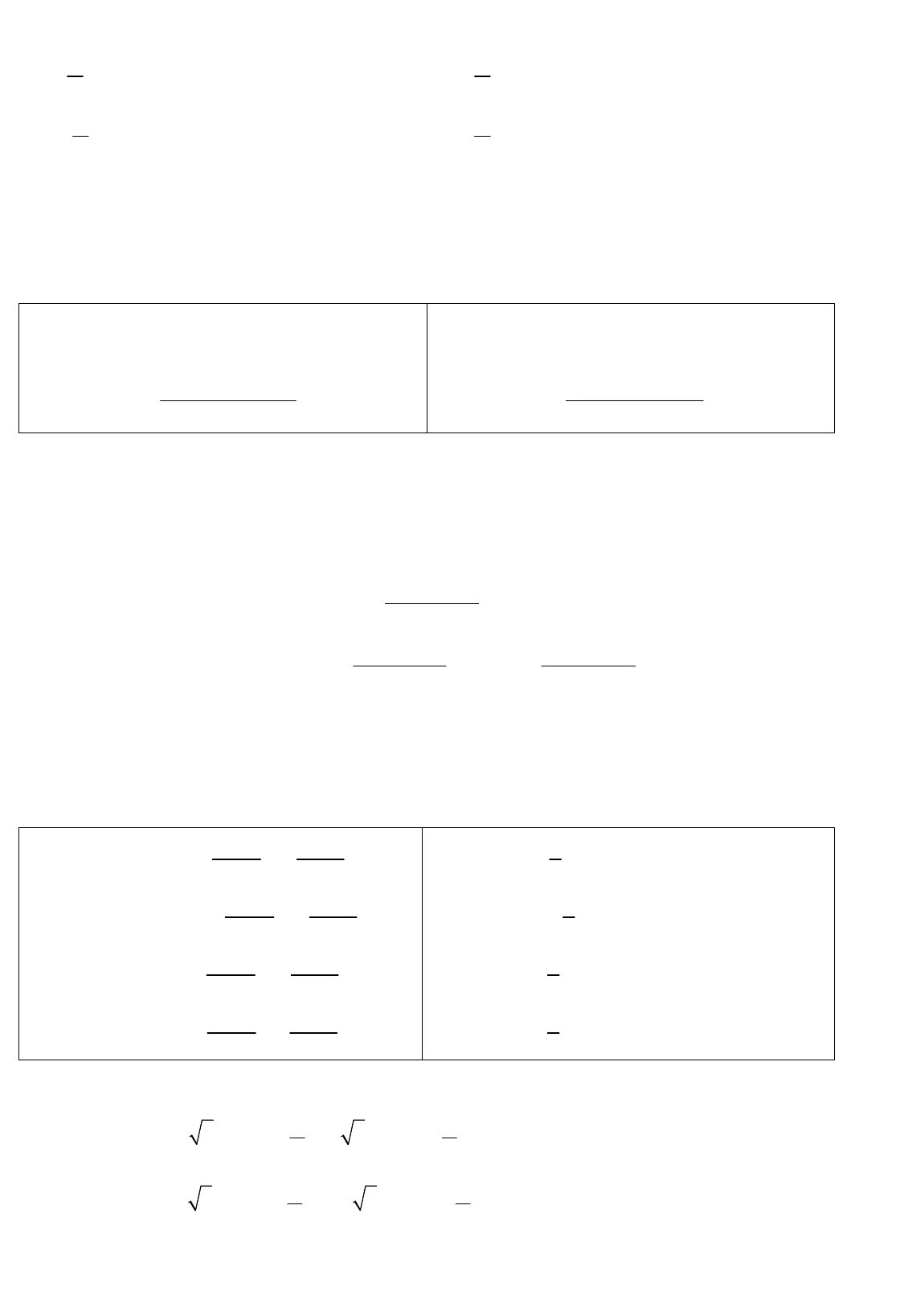Trần Mạnh Hân (0974514498) FB: thayHanSP1 Trường THPT Nguyễn Hữu Tiến – Duy Tiên – Hà Nam 2sin( ) cos2x x  cos( ) sin2x x   tan( ) cot2x x   cot( ) cot2x x    Với klà số nguyên thì ta có:sin( 2 ) sinx k x  cos( 2 ) cosx k x  tan( ) tanx k x  cot( ) cotx k x IV. CÔNG THỨC CỘNGsin( ) sin cos cos sincos( ) cos cos sin sintan tantan( )1 tan tanx y x y x yx y x y x yx yx yx y     sin( ) sin cos cos sincos( ) cos cos sin sintan tantan( )1 tan tanx y x y x yx y x y x yx yx yx y     Đặc biệt:TH1: Công thức góc nhân đôi:2 2 2 22sin 2 2 sin coscos2 cos sin 2 cos 1 1 2 sin2 tantan 21 tanx x xx x x x xxxx     Hệ quả: Công thức hạ bậc 2: 2 21 cos2 1 cos2sin ;cos2 2x xx x  TH2: Công thức góc nhân ba: 33sin 3 3 sin 4 sincos 3 4 cos 3 cosx x xx x x  V. CÔNG THỨC BIẾN ĐỔI TỔNG SANG TÍCH VÀ TÍCH SANG TỔNGcos cos 2 cos cos2 2x y x yx y  cos cos 2 sin cos2 2x y x yx y   sin sin 2 sin cos2 2x y x yx y  sin sin 2 cos sin2 2x y x yx y  1cos cos cos( ) cos( )2x y x y x y      1sin sin cos( ) cos( )2x y x y x y       1sin cos sin( ) sin( )2x y x y x y      1cos sin sin( ) sin( )2x y x y x y      Chú ý: sin cos 2 sin 2 cos4 4x x x x                    sin cos 2 sin 2 cos4 4x x x x                    ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 Trường THPT Nguyễn Hữu Tiến – Duy Tiên – Hà Nam 3  2sin sin2u v ku vu v k      2cos cos2u v ku vu v k     tan tan2u v ku vu k     cot cotu v ku vu k  Đặc biệt:sin 0sin 1 22sin 1 22x x kx x kx x k           cos 02cos 1 2cos 1 2x x kx x kx x k          Chú ý: Điều kiện có nghiệm của phương trình sinx mvàcosx mlà:1 1m  . Sử dụng thành thạo câu thần chú ” Cos đối – Sin bù – Phụ chéo” để đưa các phương trình dạng sau về phương trình cơ bản:sin cos sin sin2u v u v      cos sin cos cos2u v u v     sin sin sin sin( )u v u v     cos cos cos cos( )u v u v     Đối với phương trình 22cos 1 cos 1sin 1sin 1x xxx   không nên giải trực tiếp vì khi đó phải giải 4phương trình cơ bản thành phần, khi đó việc kết hợp nghiệm sẽ rất khó khăn. Ta nên dựa vào côngthức2 2sin cos 1x x để biến đổi như sau:22cos 1 sin 0sin 2 0cos 0sin 1x xxxx   . Tương tự đối với phương trình 22221cos2 cos 1 02cos2 011 2 sin 0sin2xxxxx    .Bài 1. Giải các phương trình sau  2cos4 2x      2 sin 2 3 06x     2 cos 2 03x     3 tan 33x   Hướng dẫn giải: 2 3cos cos cos4 2 4 4x x                     PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN