Download.vn Học tập Lớp 11 Toán 11
Bạn đang đọc: Phương pháp giải toán quan hệ vuông góc trong không gian
Phương pháp giải toán quan hệ vuông góc trong không gian Cách giải toán Hình học 11 chương 3
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Download.vn xin giới thiệu đến quý thầy cô giáo cùng các bạn học sinh lớp 11 tài liệu Phương pháp giải toán quan hệ vuông góc trong không gian được chúng tôi đăng tải sau đây.
Tài liệu bao gồm 83 trang, tóm tắt toàn bộ phương pháp giải các dạng toán và bài tập tự luận – trắc nghiệm có đáp án chủ đề Quan hệ vuông góc trong chương trình Hình học 11 chương 3. Hi vọng với tài liệu này các bạn có thêm nhiều tài liệu tham khảo, củng cố kiến thức môn Toán để đạt được kết quả cao trong bài thi học kì 1 sắp tới. Sau đây là nội dung chi tiết, mời các bạn cùng theo dõi tại đây.
Phương pháp giải toán quan hệ vuông góc lớp 11
Mục lụcChương 3 VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONGKHÔNG GIAN 5§1. Đường thẳng vuông góc với đường thẳng. Đường thẳng vuông góc với mặt phẳng 5I. Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51. Đường thẳng vuông góc với đường thẳng. Đường thẳng vuông gócvới mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52. Mặt phẳng trung trực của đoạn thẳng: . . . . . . . . . . . . . . . 5II. Các dạng toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6§2. Hai mặt phẳng vuông góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30I. Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301. Hai mặt phẳng vuông góc . . . . . . . . . . . . . . . . . . . . . . 302. Các định lý quan trọng . . . . . . . . . . . . . . . . . . . . . . . 303. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương . . . . . 314. Hình chóp đều và hình chóp cụt đều . . . . . . . . . . . . . . . . 325. Trục của đường tròn ngoại tiếp tam giác . . . . . . . . . . . . . . 34II. Các dạng toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34§3. Khoảng cách . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59I. Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 591. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng 592. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa haimặt phẳng song song . . . . . . . . . . . . . . . . . . . . . . . . . 603. Khoảng cách giữa hai đường thẳng chéo nhau . . . . . . . . . . . 60II. Các dạng toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61§4. Diện tích hình chiếu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83I. Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83II. Bài tập tự luyện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84§5. Ôn tập chương III . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 853
Chương 3VECTƠ TRONG KHÔNG GIAN.QUAN HỆ VUÔNG GÓC TRONGKHÔNG GIAN§1. Đường thẳng vuông góc với đường thẳng. Đườngthẳng vuông góc với mặt phẳngI. Tóm tắt lý thuyết1. Đường thẳng vuông góc với đường thẳng. Đường thẳng vuông góc với mặt phẳngĐịnh nghĩa 1• Đường thẳng a vuông góc với đường thẳng b nếu góc giữa a và b bằng 90◦.• Đường thẳng d vuông góc với mặt phẳng (α) nếu nó vuông góc với mọi đường thẳngnằm trong mp(α).2. Mặt phẳng trung trực của đoạn thẳng:Định nghĩa 2Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng (α) vuông góc với AB tại trungđiểm của AB.Tính chất 1Nếu (α) là mặt phẳng trung trực của AB thì: ∀M ∈ (α) ⇔ MA = MB.5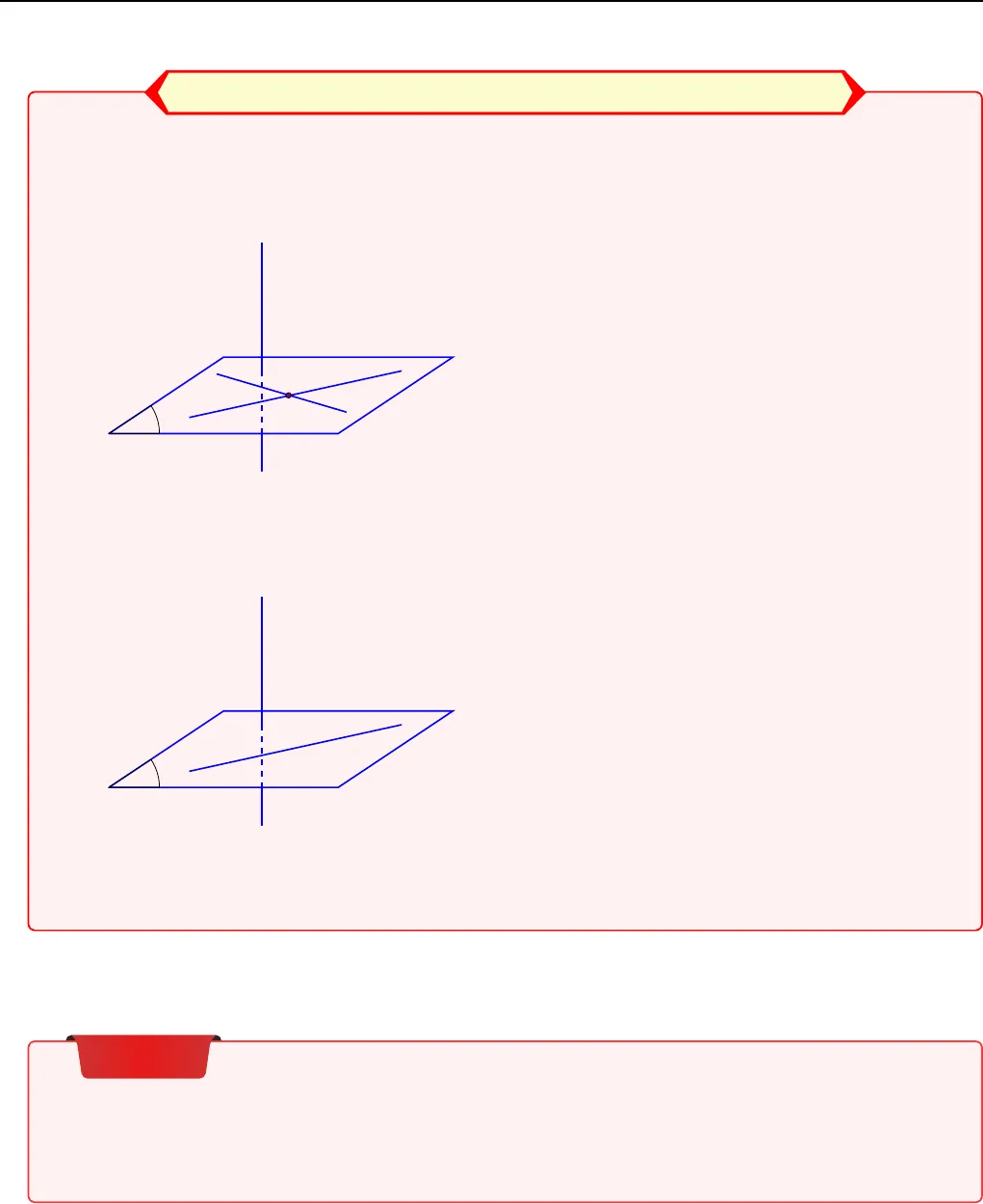
Chương 3. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN 6II. Các dạng toánDạng 1: Đường vuông góc đường. Đường vuông góc mặt¬ Đường thẳng vuông góc với mặt phẳng:Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mp(α) thì đườngthẳng a vuông góc với mp(α).dabIαd 6⊂ (α)d ⊥ a, ba ∩ b = Ia, b ⊂ (α)⇒ d ⊥ (α) Đường thẳng vuông góc với đường thẳng:Nếu đường thẳng d vuông góc với mặt phẳng (α) thì d vuông góc với tất cả các đườngthẳng nằm trong (α).daαd 6⊂ (α)d ⊥ (α)a ⊂ (α)⇒ d ⊥ a4!Lưu ý:a ⊥ cc k b⇒ a ⊥ b1. Một số ví dụVí dụ 1Cho hình chóp S.ABCD là hình vuông và SA ⊥ (ABCD).CMR: BC ⊥ (SAB).a) CMR: BD ⊥ (SAC).b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Thầy NGUYỄN NGỌC DŨNG Tel: 0976071956