Download.vn Học tập Lớp 12

Bạn đang đọc: Phương pháp viết nhanh phương trình tiếp tuyến tại một điểm của đồ thị hàm số

Phương pháp viết nhanh phương trình tiếp tuyến tại một điểm của đồ thị hàm số Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Mời quý thầy cô giáo cùng các bạn học sinh lớp 11, 12 cùng tham khảo tài liệu Phương pháp viết nhanh phương trình tiếp tuyến tại một điểm của đồ thị hàm số.

Đây là tài liệu hữu ích, gồm 10 trang, trình bày phương pháp viết nhanh phương trình tiếp tuyến tại một điểm của đồ thị hàm số với sự hỗ trợ của máy tính Casio. Tài liệu gồm phần trình bày phương pháp, 8 bài tập mẫu có hướng dẫn giải và 24 bài tập tự luyện. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.

Viết nhanh phương trình tiếp tuyến tại một điểm của đồ thị hàm số

GV : Hoàng Trọng Tấn , Tân Phú , TPHCM , Nhận dạy Luyện Thi Toán THPT Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : tracnghiemtoan– T(100) pp phân rã Nhóm luyện thi THPTQG tại Tân Phú , TPHCM , T4 , T6 : 19h-21h Phương pháp viết nhanh phương trình tiếp tuyến tại điểm của một đồ thị hàm số Bài toán : cho hàm số y f x()có đạo hàm tại mọi điểm thuộc tập xác định của nó , hãy viếtphương trình tiếp tuyến của hàm số này tại một điểm x0thuộc tập xác định của nó Lời giải : Hệ số góc tiếp tuyến tại x0của hàm số y f x()là :k f x0′( )Phương trình tiếp tuyến tại x0của hàm số là : y k x x f x00) )((  Áp dụng : cho hàm số xyx11viết phương trình tiếp tuyến tại điểm x01Lời giải : Hệ số góc tiếp tuyến tại x01của hàm số xyx11là :k2212(1 1)Phương trình tiếp tuyến tại x01của hàm số là : y x y x1 1 1( 1) 02 2 2     PP viết nhanh phương trình tiếp tuyến tại x0Cơ sở lý thuyết : Ta có phương trình hoành độ giao điểm của hàm số y f x()với chính tiếp tuyến của nó là y ax bluôn có nghiệm kép chính là hoành độ giao điểm của nó , từ đó ta xây dựng 1 phương pháp tìm nhanh đường tiếp tuyến này như sau Định lý số 7 của Galois về nghiệm bội ta có : Phương trìnhTx( ) 0có nghiệm kép là x0thì phương trình Tx‘( ) 0cũng có nghiệm là x0Áp dụng : cho hàm số xyx11viết phương trình tiếp tuyến tại điểm x01Lời Giải : gọi tiếp tuyến cần viết có dạng y ax b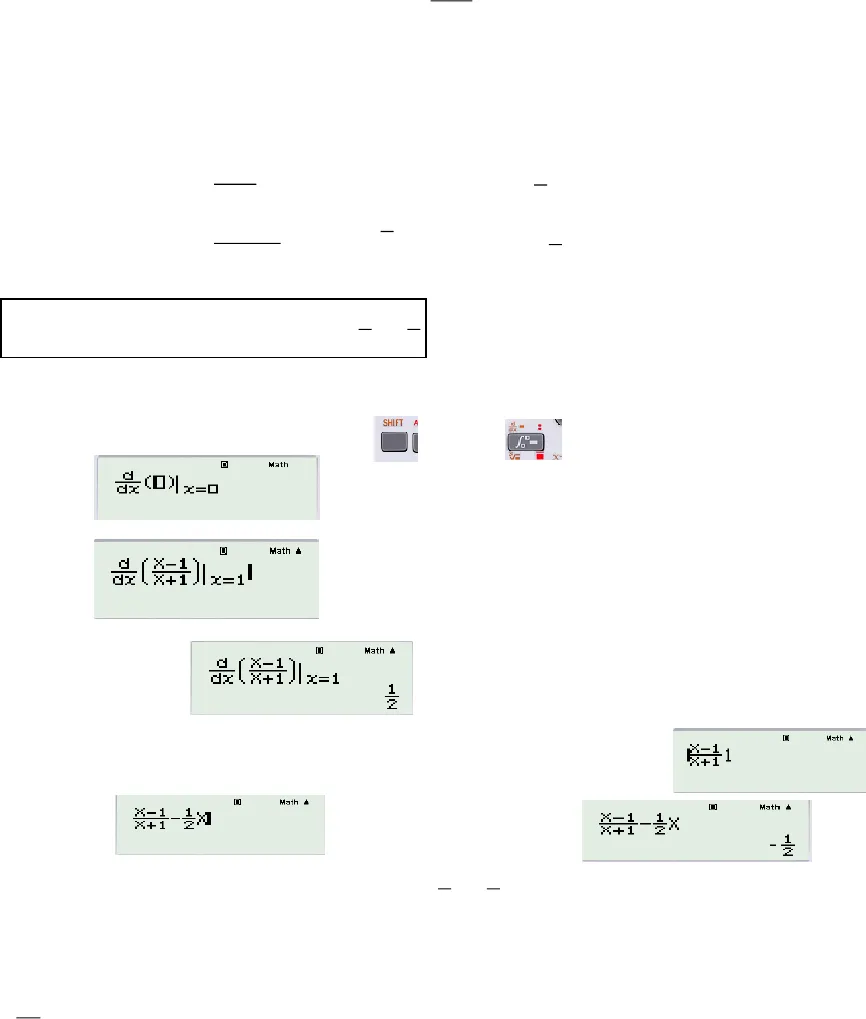GV : Hoàng Trọng Tấn , Tân Phú , TPHCM , Nhận dạy Luyện Thi Toán THPT Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : tracnghiemtoan– T(100) pp phân rã Nhóm luyện thi THPTQG tại Tân Phú , TPHCM , T4 , T6 : 19h-21h PTHĐGD của hàm số và tiếp tuyến này là : xax bx11Theo định lý thìx01là nghiệm kép của phương trình , áp dụng Galois 7 ta có 1 là nghiệm của hệ : axxax bx22( 1)11aaabb1211202Vậy phương trình tiếp tuyến là : yx1122Chắc các bạn thấy là lâu hơn cách bt đúng ko  vậy thì làm sao gọi là nhanh đc , ok đợi mình tý Bật máy Casio hoặc Vinacal lên , nhấn và nhấn Máy hiện: Nhập : Nhấn = , máy báo : Đưa con dấu nháy của máy ra đằng trước biểu thức và nhấn nút Del Nhập vào : , rồi nhấn solve 1 máy báo Vậy phương trình tiếp tuyến cần viết là : yx1122Tóm tắt   xxxxdf x adxy ax bf x ax b00()()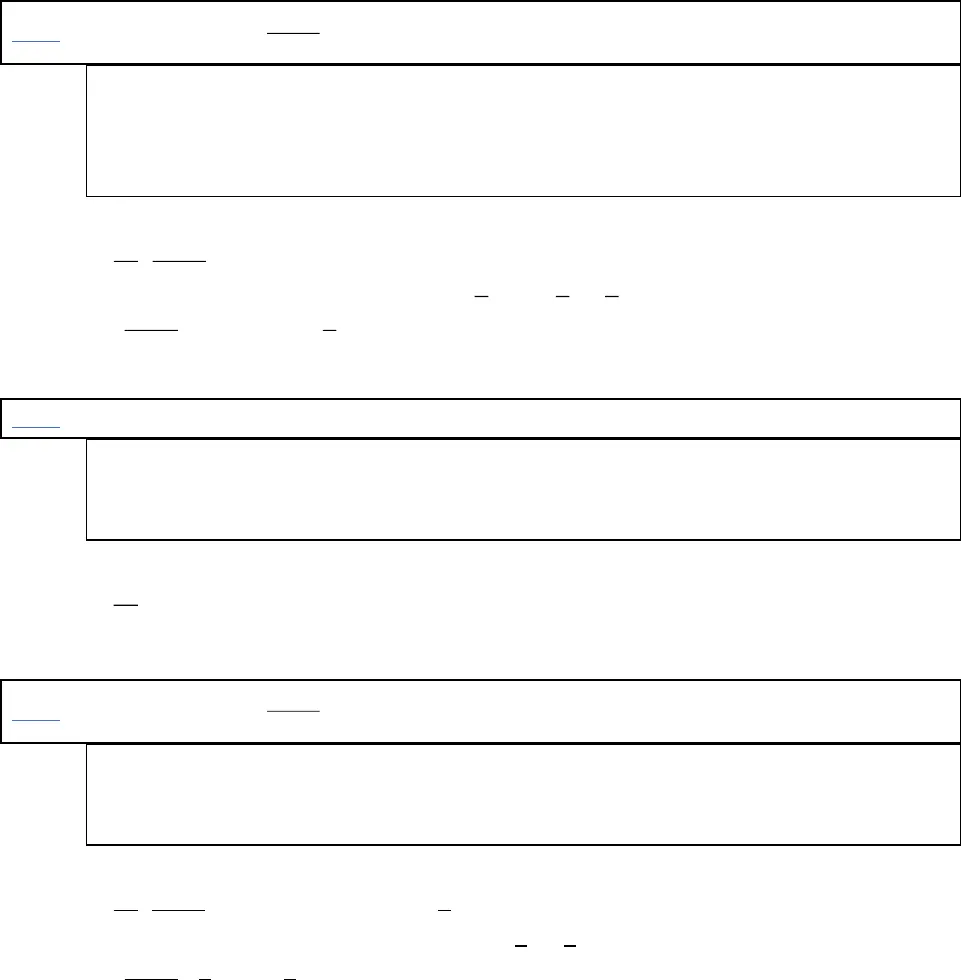  GV : Hoàng Trọng Tấn , Tân Phú , TPHCM , Nhận dạy Luyện Thi Toán THPT Tel : 0909520755 , Face : Hoàng Trọng Tấn Page : tracnghiemtoan– T(100) pp phân rã Nhóm luyện thi THPTQG tại Tân Phú , TPHCM , T4 , T6 : 19h-21h Áp dụng : BT 1. Cho hàm số: 211xyx1/ Khảo sát sự biến thiên và vẽ đồ thị ()Ccủa hàm số đã cho. 2/ Viết phương trình tiếp tuyến của đồ thị ( ),Cbiết tiếp điểm có hoành độ 1.x Đề thi minh họa THPT Quốc Gia năm 2015 – Bộ GD & ĐT Lời Giải : Nhập vào máy ta có xxdxdx xy x y xxxx11210,7511 3 10,754 4 42 1 10,7514         BT 2. Cho hàm số: 422.y x x1/ Khảo sát sự biến thiên và vẽ đồ thị ()Ccủa hàm số đã cho. 2/ Viết phương trình tiếp tuyến của ()Ctại điểm có hoành độ bằng 2.Đề thi TN THPT năm 2008 Lời Giải : Nhập vào máy ta có   xxxdxdxxyxxx2242422424 40( 24) 422 0      BT 3. Cho hàm số: 211xyx1/ Khảo sát sự biến thiên và vẽ đồ thị ()Ccủa hàm số đã cho. 2/ Viết phương trình tiếp tuyến của ()Ctại điểm có hoành độ bằng 2.Đề thi thử THPT Quốc Gia năm 2015 – THTP Lý Tự Trọng – Nam Định – Lần 2 Lời Giải : Nhập vào máy ta có xxdxdx xyxxxx222 1 10,33333333333..1311332 1 1 11 3 3    