Download.vn Học tập Lớp 11
Bạn đang đọc: Phương pháp xác định giao điểm, giao tuyến, thiết diện trong không gian
Phương pháp xác định giao điểm, giao tuyến, thiết diện trong không gian Tài liệu ôn tập môn Toán lớp 11
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Phương pháp xác định giao điểm, giao tuyến, thiết diện trong không gian là tài liệu cực kì hữu ích đối với các bạn học sinh lớp 11 và lớp 12.
Tài liệu hướng dẫn phương pháp xác định giao điểm, giao tuyến và thiết diện trong hình học không gian thông qua các bài tập có lời giải chi tiết. Hi vọng qua tài liệu này các bạn học sinh lớp 12 có thêm nhiều tài liệu tham khảo, củng cố kiến thức để đạt được kết quả cao trong các bài kiểm tra sắp tới. Mời các bạn cùng theo dõi và tải tài liệu tại đây.
Phương pháp xác định giao điểm, giao tuyến, thiết diện
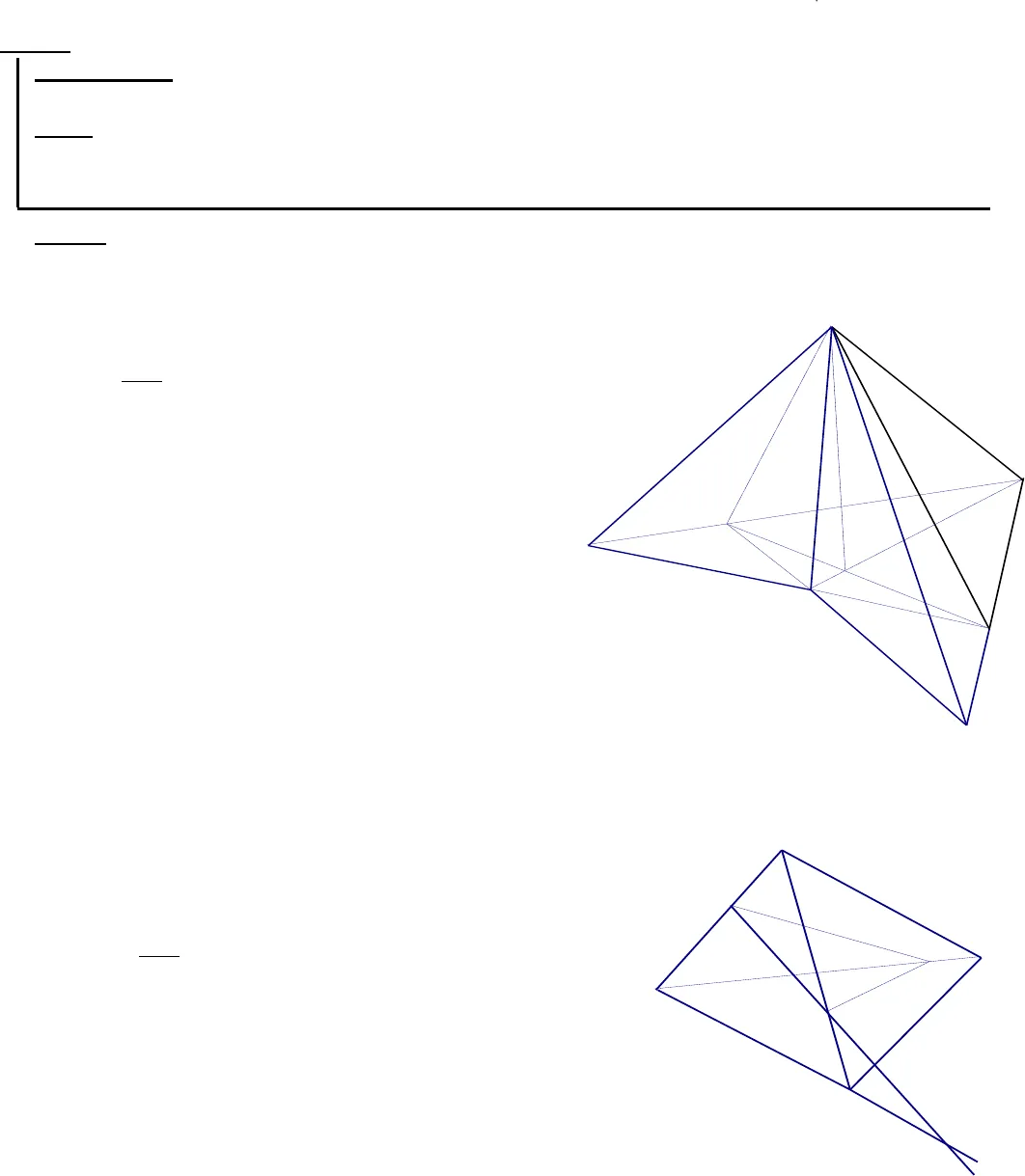Bài tập chương 2 Dạng 1 : Xác định giao tuyến của hai mặt phẳng () và () Phương pháp : Tìm hai điểm chung phân biệt của hai mặt phẳng () và () Đường thẳng đi qua hai điểm chung ấy là giao tuyến cần tìm Chú ý : Để tìm chung của () và () thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng Bài tập : 1. Trong mặt phẳng () cho tứ giácABCDcó các cặp cạnh đối không song song và điểm )(S. a. Xác định giao tuyến của)(SACvà (SBD) b. Xác định giao tuyến của (SAB) và (SCD) c. Xác định giao tuyến của (SAD) và (SBC) Giải a. Xác định giao tuyến của (SAC) và (SBD) Ta có : S là điểm chung của (SAC) và (SBD) Trong (), gọi O = AC BD O AC mà AC(SAC)O (SAC) O BD mà BD(SBD)O (SBD) O là điểm chung của (SAC) và (SBD) Vậy : SO là giao tuyến của (SAC) và (SBD) b. Xác định giao tuyến của (SAB) và (SCD) Ta có: S là điểm chung của (SAC) và (SBD) Trong () , AB không song song với CD Gọi I = AB CD I AB mà AB (SAB)I (SAB) I CD mà CD(SCD)I (SCD) I là điểm chung của (SAB) và (SCD) Vậy : SI là giao tuyến của (SAB) và (SCD) c. Tương tự câu a, b 2. Cho bốn điểm A,B,C,D không cùng thuộc một mặt phẳng . Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của ( BCD) và ( MNP) Giải P BD mà BD( BCD) P ( BCD) P ( MNP) P là điểm chung của ( BCD) và ( MNP) Trong mp (ABC) , gọi E = MN BC E BC mà BC( BCD) E ( BCD) E MN mà MN( MNP) E ( MNP) E là điểm chung của ( BCD) và ( MNP) Vậy : PE là giao tuyến của ( BCD) và ( MNP)kSIDOBCAJCBENDPMA
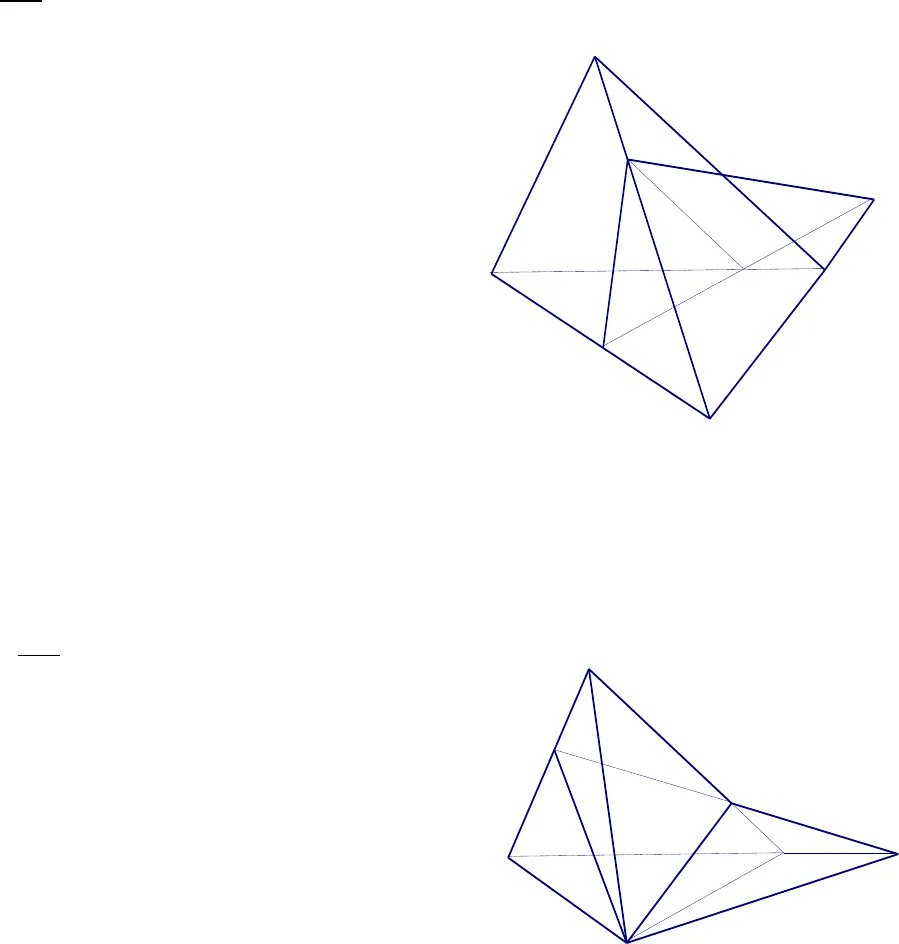3. Cho tam giác ABC và một điểm S không thuộc mp (ABC ) , một điểm I thuộc đoạn SA . Một đường thẳng a không song song với AC cắt các cạnh AB, BC theo thứ tự tại J , K. Tìm giao tuyến của các cặp mp sau : a. mp ( I,a) và mp (SAC ) b. mp ( I,a) và mp (SAB ) c. mp ( I,a) và mp (SBC ) Giải a. Tìm giao tuyến của mp ( I,a) với mp (SAC ) : Ta có:ISA mà SA(SAC )I(SAC ) I( I,a) I là điểm chung của hai mp ( I,a) và (SAC ) Trong (ABC ), a không song song với AC Gọi O = a AC O AC mà AC(SAC )O (SAC ) O ( I,a) O là điểm chung của hai mp ( I,a) và (SAC ) Vậy : IO là giao tuyến của hai mp ( I,a) và (SAC ) b. Tìm giao tuyến của mp ( I,a) với mp (SAB) : là JI c. Tìm giao tuyến của mp ( I,a) với mp (SBC ) Ta có : K là điểm chung của hai mp ( I,a) và mp (SBC ) Trong mp (SAC) , gọi L = IO SC L SC mà SC(SBC )L (SBC ) L IO mà IO( I,a)L ( I,a ) L là điểm chung của hai mp ( I,a) và (SBC ) Vậy: KL là giao tuyến của hai mp ( I,a) và (SBC ) 4. Cho bốn điểm A ,B ,C , D không cùng nằm trong một mp a. Chứng minh AB và CD chéo nhau b. Trên các đoạn thẳng AB và CD lần lượt lấy các điểm M, N sao cho đường thẳng MN cắt đường thẳng BD tại I . Hỏi điểm I thuộc những mp nào .Xđ giao tuyến của hai mp (CMN) và ( BCD) Giải a. Chứng minh AB và CD chéo nhau : Giả sử AB và CD không chéo nhau Do đó có mp () chứa AB và CD A ,B ,C , D nằm trong mp () mâu thuẩn giả thuyết Vậy : AB và CD chéo nhau b. Điểm I thuộc những mp : I MN mà MN(ABD )I (ABD )I MN mà MN(CMN )I (CMN )I BD mà BD(BCD )I (BCD ) Xđ giao tuyến của hai mp (CMN) và ( BCD) là CI 5. Cho tam giác ABC nằm trong mp ( P) và a là mộtđường thẳng nằm trong mp ( P) và không song song với AB và AC . S là một điểm ở ngoài mặt phẳng ( P) và A’ là một điểm thuộc SA .LABJCKOISMICBDNA
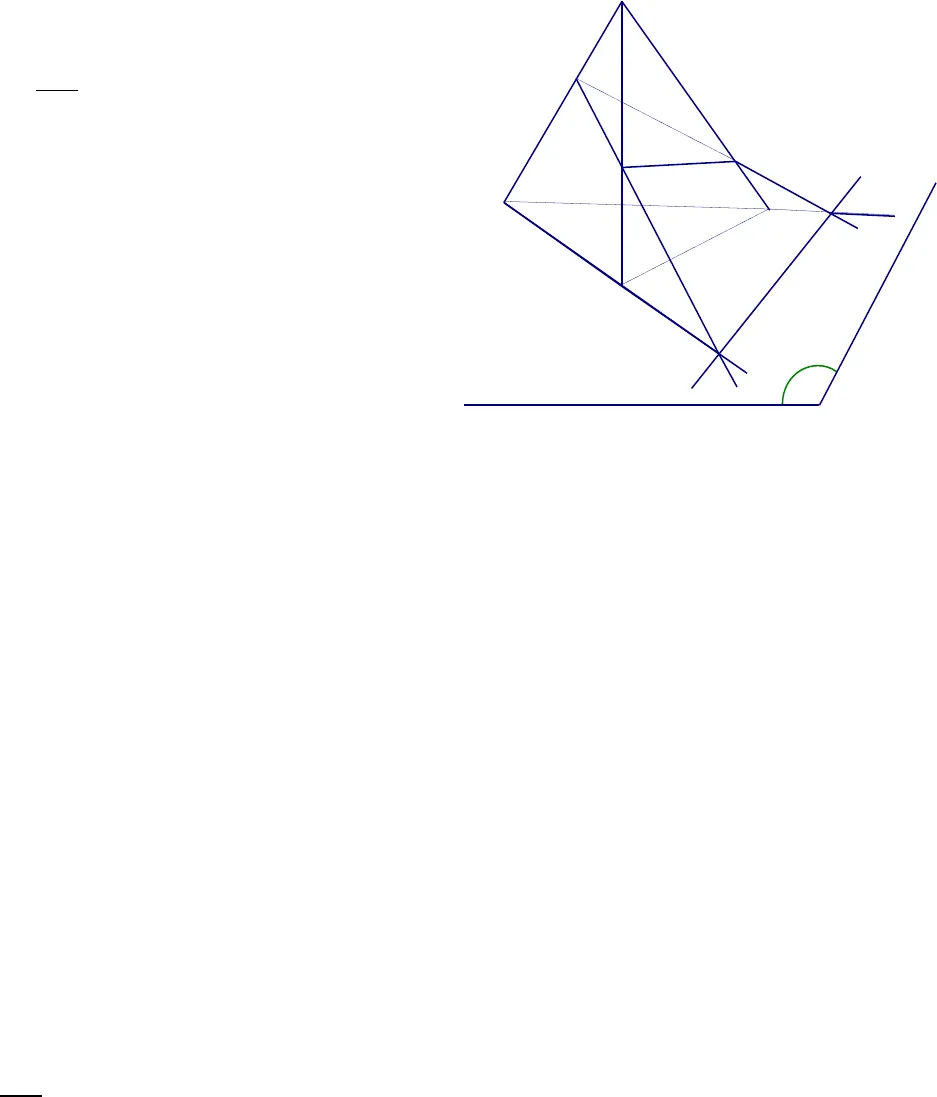Xđ giao tuyến của các cặp mp sau a. mp (A’,a) và (SAB) b. mp (A’,a) và (SAC) c. mp (A’,a) và (SBC) Giải a. Xđ giao tuyến của mp (A’,a) và (SAB) A’ SA mà SA( SAB)A’( SAB) A’ ( A’,a) A’ là điểm chung của ( A’,a) và (SAB ) Trong ( P) , ta có a không song song với AB Gọi E = a AB E AB mà AB (SAB )E (SAB ) E ( A’,a) E là điểm chung của ( A’,a) và (SAB ) Vậy: A’E là giao tuyến của ( A’,a) và (SAB ) b. Xđ giao tuyến của mp (A’,a) và (SAC) A’ SA mà SA( SAC)A’( SAC)A’ ( A’,a) A’ là điểm chung của ( A’,a) và (SAC ) Trong ( P) , ta có a không song song với AC Gọi F = a AC FAC mà AC(SAC )F (SAC ) E ( A’,a) F là điểm chung của ( A’,a) và (SAC ) Vậy: A’F là giao tuyến của ( A’,a) và (SAC ) c. Xđ giao tuyến của (A’,a) và (SBC) Trong (SAB ) , gọi M = SB A’E M SB mà SB( SBC)M( SBC) M A’E mà A’E ( A’,a) M( A’,a) M là điểm chung của mp ( A’,a) và (SBC ) Trong (SAC ) , gọi N = SC A’F N SC mà SC( SBC) N( SBC) N A’F mà A’F ( A’,a) N( A’,a) N là điểm chung của mp ( A’,a) và (SBC ) Vậy: MN là giao tuyến của ( A’,a) và (SBC ) 6. Cho tứ diện ABCD , M là một điểm bên trong tam giác ABD , N là một điểm bên trong tam giác ACD . Tìm giao tuyến của các cặp mp sau a. (AMN) và (BCD) b. (DMN) và (ABC ) Giải a. Tìm giao tuyến của (AMN) và (BCD) Trong (ABD ) , gọi E = AM BD E AM mà AM( AMN)E( AMN) E BD mà BD( BCD)E( BCD) E là điểm chung của mp ( AMN) và (BCD ) FaPEBCNMAA’S