Tam giác vuông cân là một trong những kiến thức cơ bản trong chương trình Toán THCS và thường xuất hiện trong các bài thi vào lớp 10.
Bạn đang đọc: Tam giác vuông cân
Tổng hợp kiến thức về tam giác vuông cân dưới đây gồm khái niệm, tính chất, cách tính đường cao và diện tích tam giác vuông cân kèm theo các dạng bài tập tự luyện. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập về chứng minh tam giác vuông cân. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các em xem thêm một số tài liệu như: chứng minh phương trình luôn có nghiệm với mọi m, chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng.
Tam giác vuông cân
1. Tam giác vuông cân là gì
– Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân hay nói cách khác tam giác vuông là tam giác có 2 cạnh vuông góc và bằng nhau.
– Tam giác ABC có AB = AC, AB ⊥ AC thì tam giác ABC vuông cân tại A.
2. Tính chất tam giác vuông cân
Tam giác vuông cân đồng thời là một tam giác vuông và cũng là tam giác cân. Ở tam giác vuông cân sẽ có hai góc nhọn, 1 góc vuông và có hai cạnh góc vuông bằng nhau. Mỗi góc nhọn trong tam giác vuông cân có độ lớn là 45 độ.
Với định nghĩa trên, tam giác vuông cân có những tính chất sau đây:
– Tam giác vuông cân sẽ có 2 góc đáy bằng nhau, đều bằng 45 độ.
– Tam giác vuông có 3 đường là đường cao, đường phân giác tính từ đỉnh góc vuông và đường trung tuyến sẽ trùng với nhau và 2 đường thẳng này sẽ có độ dài bằng nửa cạnh huyền.
3. Đường cao tam giác vuông cân
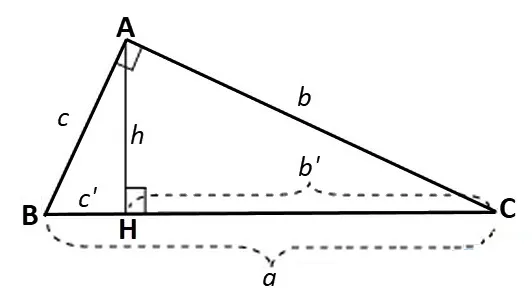
Công thức tính cạnh và đường cao trong tam giác vuông cân
Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
b’ là đường chiếu của cạnh b trên cạnh huyền; c’ là đường chiếu của cạnh c trên cạnh huyền;
h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.
Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán.
Công thức tính cạnh huyền tam giác vuông cân
Theo định lý pitago, công thức tính cạnh huyền tam giác vuông cân bằng căn bậc hai của bình phương hai cạnh còn lại
Trong đó:
c là cạnh huyền của tam giác vuông cân
a, b lần lượt là 2 cạnh còn lại
Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán
4. Tính diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:
Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:
5. Cách chứng minh tam giác vuông cân
Từ định nghĩa về tam giác vuông cân ta có các cách chứng minh tam giác vuông cân như sau:
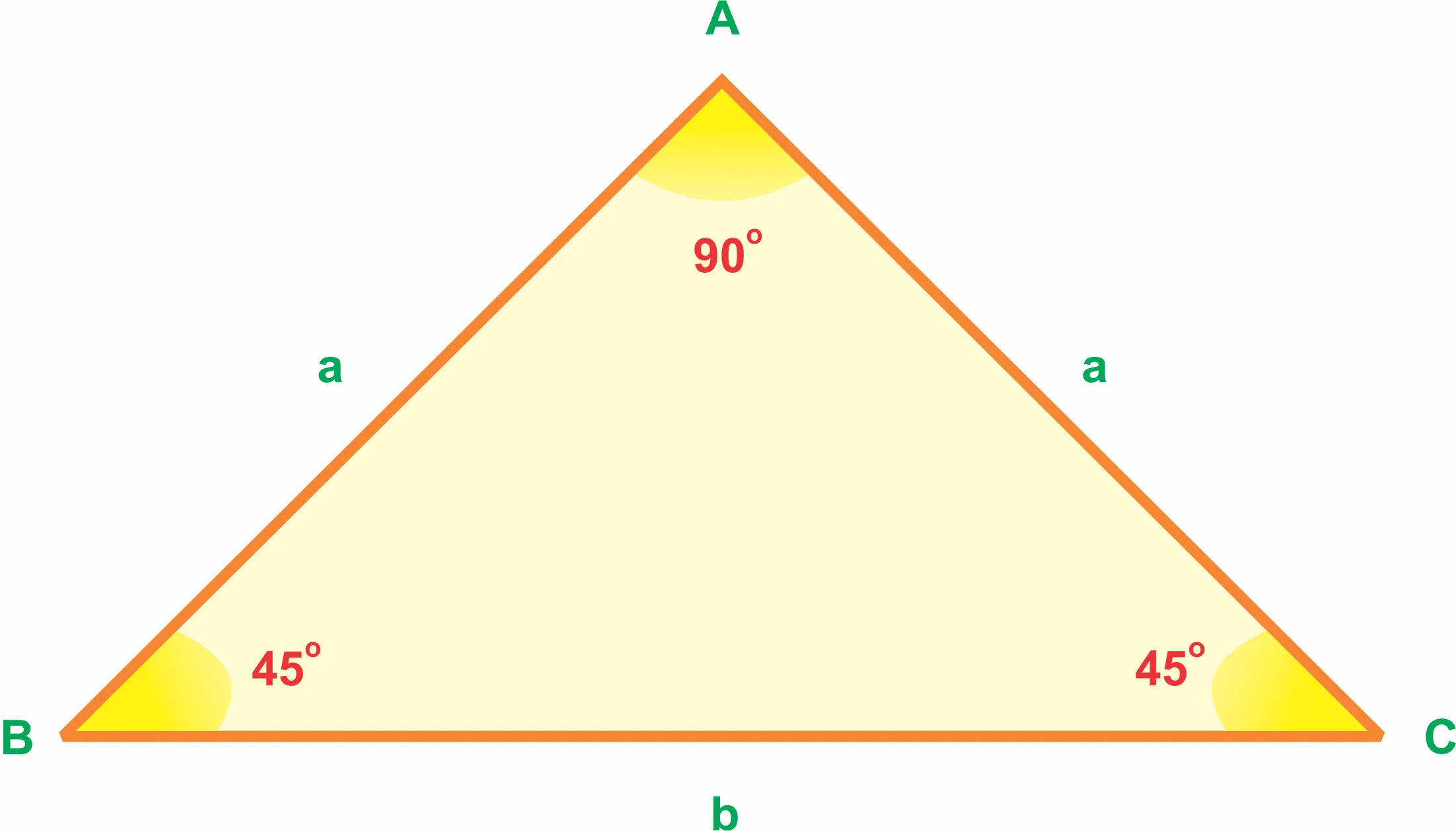
– Tam giác có 1 góc vuông và 2 cạnh góc vuông bằng nhau là tam giác vuông cân
– Tam giác vuông có 1 góc nhọn bằng 45 độ
– Tam giác có 2 cạnh bằng nhau và 1 góc đáy bằng 45 độ
6. Ví dụ tam giác vuông cân
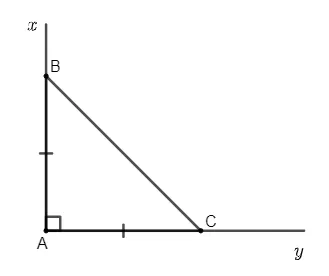
Ví dụ 1: Vẽ tam giác ABC vuông cân tại A.
Giải:
– Vẽ góc vuông xAy
– Trên tia Ax lấy điểm B, trên tia Ay lấy điểm C sao cho AB = AC
– Nối B với C
– Khi đó ta được tam giác ABC vuông cân tại A.
7. Bài tập về tam giác vuông cân
Trước khi đi trực tiếp đến giải các bài tập liên quan đến tam giác vuông cân các bạn tham khảo một số dạng bài cơ bản và phổ biến nhất:
Dạng 1: Nhận biết một tam giác cho trước bất kỳ là tam giác cân, tam giác đều hoặc vuông cân
Cách giải: Dựa theo dấu hiệu nhận biết / cách chứng minh từng loại tam giác. Trước hết nên phán đoán để tìm ra cách giải nhanh nhất
Dạng 2: Chứng minh các tính chất của tam giác được cho ví dụ là: tính độ dài của cạnh, độ dài của góc, chứng minh sự bằng nhau của tam giác,….
Cách giải: Để giải dạng toán này, bạn cần vận dụng kiến thức là tính chất của các tam giác này cùng với dữ liệu đề bài là có thể tìm ra đáp án.
Bài 1:
a. Một tam giác cân có một góc là 800. Số đo của hai góc còn lại là bao nhiêu?
b. Một tam giác cân có một góc là 1000. Số đo của hai góc còn lại là bao nhiêu?
Bài 2: Cho tam giác ABC nhọn (AB
Bài 3: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm E sao cho . Trên tia BE lấy điểm M sao cho EM = BC. So sánh hai góc
.
Bài 4: Cho tam giác ABC cân tại A có góc B = 60 độ và AB = 5 cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC (E thuộc BC).
a. Chứng minh tam giác ABD = tam giác EBD.
b. Chứng minh tam giác ABE là tam giác đều.
c. Chứng minh tam giác AEC là tam giác cân.
d. Tính độ dài cạnh AC.
Bài 5: Cho tam giác ABC có số đo góc A là 1200. Trên đờng phân giác AD của góc A lấy điểm I. Trên tia đối của AC và AB lấy điểm E và F sao cho AE = AF = AI.
a. Chứng minh rằng: AB và AC là trung trực của IE và IF.
b. Chứng minh rằng tam giác IEF đều.
c. Chứng minh rằng AI ⊥ EF.
Bài 6: Cho tam giác ABC cân tại A có góc A 0. Kẻ BD vuông góc với AC. Trên AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
a) DE // BC
b) CE vuông góc với AB.
Bài 7: Cho tam giác ABC có BC

