Download.vn Học tập Lớp 12

Bạn đang đọc: Tập hợp biểu diễn số phức

Tập hợp biểu diễn số phức Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Tập hợp biểu diễn số phức là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.

Tài liệu do thầy Trần Văn Toàn biên soạn gồm 37 trang với nội dung chủ đạo là các bài toán liên quan đến tập hợp biểu diễn số phức. Tài liệu nêu rõ các tính chất cần nắm để giải quyết các bài toán tìm tập hợp biểu diễn số phức, cùng với các ví dụ minh họa có lời giải chi tiết đi kèm. Ngoài ra, tài liệu còn trình bày một số kiến thức bổ trợ có liên quan. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Tập hợp biểu diễn số phức

Mục lụcChương 1. Số phức 21.1 Tập hợp biểu diễn số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21.2 Vị trí tương đối của đường thẳng và đường tròn . . . . . . . . . . . . . . . . . . . 281.3 Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28Chương 2. Tiếp tuyến 312.1 Hàm phân thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 312.2 Hàm bậc ba . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361Chương 1Số phức1.1 Tập hợp biểu diễn số phứcTính chất 1.1Cho hai số phức z và z1. Gọi M là điểm biểu diễn cho số phức z, A là điểm biểu diễncho số phức z1. Đại lượng |z −z1| là độ dài đoạn thẳng AM.Chứng minh. Gọi M(x, y), A(x1, y1). Ta có|z −z1|=q(x −x1)2+(y − y1)2.Tính chất 1.2Cho số phức z1=a +bi, tập hợp các điểm biểu diễn số phức z thoả|z −z1|=R là đườngtròn tâm I(a; b), bán kính R.Chứng minh. Gọi M(x, y). Từ giả thiết ta có(x −a)2+(y −b)2=R2.Ví dụ 1.1Tập hợp các điểm biểu diễn cho số phức z thoả |z +2 −i|= 3 là đường tròn tâm (−2,1)bán kính R =3.Ví dụ 1.2Tập hợp các điểm biểu diễn cho số phức z thoả |z +i|=1 là đường tròn tâm (0,−1) bánkính R =1.2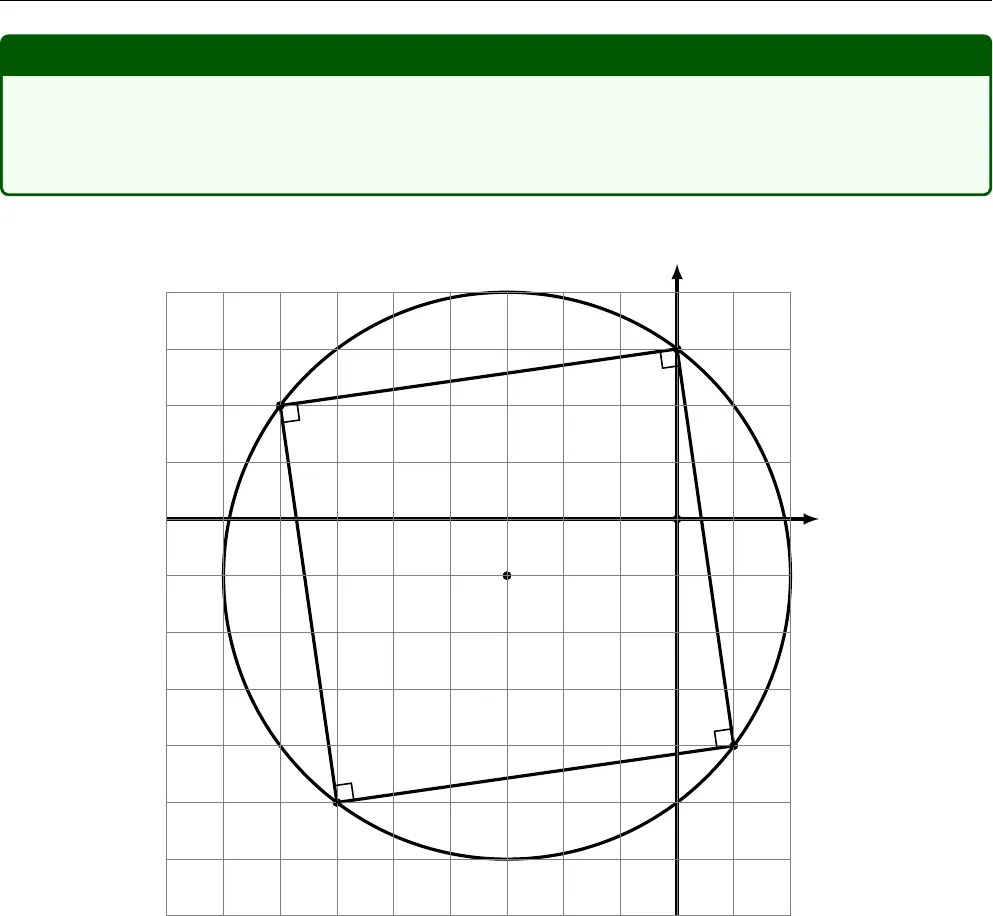1.1. Tập hợp biểu diễn số phức 3Ví dụ 1.3Cho số phức z thoả |z +3 +i|=5. Tính giá trị của biểu thứcE =|z +7 −2i|2+|z +6 +5i|2+|z −3i|2+|z −1 +4i|2.ACBTDOxyLời giải. Gọi M là điểm biểu diễn cho số phức z, thì M thuộc đường tròn tâm T(−3,−1),bán kính R =5.Xét các điểm A(−7,2), B(−6, −5), C(1, −4), D(0, 3). Ta cóE = AM2+BM2+CM2+DM2.Để ý rằng, ABCD là hình vuông có các đỉnh thuộc đường tròn, nênE = AM2+BM2+CM2+DM2=8R2=200.♦Lời bình. Cho đa giác đều A1A2... Annội tiếp trong đường tròn (C ) có tâm O, bán kính R.Với M là điểm tuỳ ý trong mặt phẳng chứa đường tròn, ta cóA1M2+A2M2+···+ AnM2= n(R2+OM2).♣