Tỉ số lượng giác của góc nhọn là tài liệu vô cùng hữu ích không thể thiếu dành cho các học sinh lớp 9 chuẩn bị thi vào 10 tham khảo.
Bạn đang đọc: Tỉ số lượng giác của góc nhọn
Tỉ số lượng giác của góc nhọn gồm đầy đủ lý thuyết và các dạng toán thường gặp, được biên soạn rất khoa học, phù hợp với mọi đối tượng học sinh có học lực từ trung bình, khá đến giỏi. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi vào lớp 10 môn Toán. Vậy sau đây là nội dung chi tiết tài liệu Tỉ số lượng giác của góc nhọn, mời các bạn cùng theo dõi tại đây.
Tỉ số lượng giác của góc nhọn
I. Tỉ số lượng giác của góc nhọn
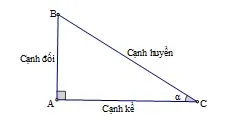
Tính chất 1:
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Tức là: Cho hai góc có
Khi đó:
Tính chất 2:
+ Nếu hai góc nhọn và
có
hoặc
thì
Tính chất 3:
+ Nếu là một góc nhọn bất kỳ thì
 0;cot alpha > 0″ width=”389″ height=”18″ data-type=”0″ data-latex=”0 0;cot alpha > 0″ data-src=”https://tex.vdoc.vn?tex=0%20%3C%20%5Csin%20%5Calpha%20%3C%201%3B0%20%3C%20%5Ccos%20%5Calpha%20%3C%201%2C%20%5Ctan%20%5Calpha%20%3E%200%3B%5Ccot%20%5Calpha%20%3E%200″>
0;cot alpha > 0″ width=”389″ height=”18″ data-type=”0″ data-latex=”0 0;cot alpha > 0″ data-src=”https://tex.vdoc.vn?tex=0%20%3C%20%5Csin%20%5Calpha%20%3C%201%3B0%20%3C%20%5Ccos%20%5Calpha%20%3C%201%2C%20%5Ctan%20%5Calpha%20%3E%200%3B%5Ccot%20%5Calpha%20%3E%200″>
II. Bảng tỉ số lượng giác các góc đặc biệt
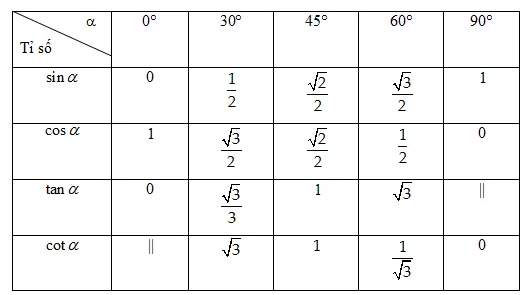
III. Các dạng toán thường gặp
Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp:
Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng giác giữa các góc
Phương pháp:
Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất “Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia”)
Bước 2: Với góc nhọn ta có:
 beta ;” width=”185″ height=”19″ data-type=”0″ data-latex=”cos alpha beta ;” data-src=”https://tex.vdoc.vn?tex=%5Ccos%20%5Calpha%20%3C%20%5Ccos%20%5Cbeta%20%5CLeftrightarrow%20%5Calpha%20%3E%20%5Cbeta%20%3B”>
beta ;” width=”185″ height=”19″ data-type=”0″ data-latex=”cos alpha beta ;” data-src=”https://tex.vdoc.vn?tex=%5Ccos%20%5Calpha%20%3C%20%5Ccos%20%5Cbeta%20%5CLeftrightarrow%20%5Calpha%20%3E%20%5Cbeta%20%3B”>
 beta” width=”179″ height=”19″ data-type=”0″ data-latex=”cot alpha beta” data-src=”https://tex.vdoc.vn?tex=%5Ccot%20%5Calpha%20%3C%20%5Ccot%20%5Cbeta%20%5CLeftrightarrow%20%5Calpha%20%3E%20%5Cbeta”>
beta” width=”179″ height=”19″ data-type=”0″ data-latex=”cot alpha beta” data-src=”https://tex.vdoc.vn?tex=%5Ccot%20%5Calpha%20%3C%20%5Ccot%20%5Cbeta%20%5CLeftrightarrow%20%5Calpha%20%3E%20%5Cbeta”>
Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác
Phương pháp:
Ta thường sử dụng các kiến thức
+ Nếu là một góc nhọn bất kỳ thì
 0;cot alpha > 0 , {sin ^2}alpha + {cos ^2}alpha = 1;tan alpha .cot alpha = 1″ width=”675″ height=”22″ data-type=”0″ data-latex=”0 0;cot alpha > 0 , {sin ^2}alpha + {cos ^2}alpha = 1;tan alpha .cot alpha = 1″ data-src=”https://tex.vdoc.vn?tex=0%20%3C%20%5Csin%20%5Calpha%20%3C%201%3B0%20%3C%20%5Ccos%20%5Calpha%20%3C%201%2C%20%5Ctan%20%5Calpha%20%3E%200%3B%5Ccot%20%5Calpha%20%3E%200%20%2C%20%7B%5Csin%20%5E2%7D%5Calpha%20%2B%20%7B%5Ccos%20%5E2%7D%5Calpha%20%3D%201%3B%5Ctan%20%5Calpha%20.%5Ccot%20%5Calpha%20%3D%201″>
0;cot alpha > 0 , {sin ^2}alpha + {cos ^2}alpha = 1;tan alpha .cot alpha = 1″ width=”675″ height=”22″ data-type=”0″ data-latex=”0 0;cot alpha > 0 , {sin ^2}alpha + {cos ^2}alpha = 1;tan alpha .cot alpha = 1″ data-src=”https://tex.vdoc.vn?tex=0%20%3C%20%5Csin%20%5Calpha%20%3C%201%3B0%20%3C%20%5Ccos%20%5Calpha%20%3C%201%2C%20%5Ctan%20%5Calpha%20%3E%200%3B%5Ccot%20%5Calpha%20%3E%200%20%2C%20%7B%5Csin%20%5E2%7D%5Calpha%20%2B%20%7B%5Ccos%20%5E2%7D%5Calpha%20%3D%201%3B%5Ctan%20%5Calpha%20.%5Ccot%20%5Calpha%20%3D%201″>
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

