Download.vn Học tập Lớp 11 Toán 11

Bạn đang đọc: Tính giá trị và chứng minh các biểu thức tổ hợp

Tính giá trị và chứng minh các biểu thức tổ hợp Tài liệu ôn tập môn Toán lớp 11

Giới thiệu Tải về Bình luận

• 1

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Với mong muốn giúp các bạn có thêm tư liệu cho việc tự học, Download.vn xin giới thiệu tài liệu Tính giá trị và chứng minh các biểu thức tổ hợp lớp 11.

Chứng minh đẳng thức và tính giá trị biểu thức trong giải tích tổ hợp là một vấn đề khá rộng, nó có mặt trong những bài thi THPT và cả trong các đề thi HSG Quốc gia. Trong chuyên đề này hầu hết là liên quan đến tổ hợp nên các bạn học sinh lớp 11, 12 cần nắm vững và sử dụng thuần thục 3 công thức liên quan đến tổ hợp. Sau đây là nội dung chi tiết tài liệu, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Tính giá trị và chứng minh các biểu thức tổ hợp

1CHỨNG MINH ĐẲNG THỨCTÍNH GIÁ TRỊ BIỂU THỨCMai Ngọc Thắng – A1 (08-11) THPT NTMK, Tp.HCMChứng minh đẳng thức và tính giá trị biểu thức trong giải tích tổ hợp là một vấn đề khá rộng, nócó mặt trong những bài thi ĐH và cả trong các đề thi HSGQG. Với mong muốn giúp các bạn cóthêm tư liệu cho việc tự học, đây là những kiến thức tôi có được trong quá trình luyện thi vớingười thầy kính yêu Vũ Vĩnh Thái và thêm một ít tôi sưu tầm được, tôi xin tổng hợp lại thànhmột chuyên đề nho nhỏ cũng nhằm thêm mục đích là lưu trữ. Mọi góp ý xin liên hệ qua email[email protected] hoặc nick yahoo blackjack2512.I. Vài công thức cần nhớ:_ Chỉnh hợp:!( )!knnAn k_ Tổ hợp:!!( )!knnCk n k_ Tính chất của tổ hợp:k n kn nC CHằng đẳng thức Pascal:1 11k k kn n nC C C  _ Nhị thức Newton:0( )nn k n k knka b C a b Trong chuyên đề này hầu hết là liên quan đến tổ hợp nên các bạn cần nắm vững và sử dụngthuần thục 3 công thức liên quan đến tổ hợp như trên và trong từng mục tôi sẽ nhắc lại công thứcáp dụng trong các bài tập thuộc mục đó.II. Các phương pháp và ví dụ minh họa:Các bài tập tôi nêu ra đều minh họa khá rõ cho phương pháp và sẽ có một số bài tập để các bạncó thể rèn luyện lại. Tôi sẽ cố gắng phân tích hướng giải ở một số bài toán với mong muốn giúpcác bạn hiểu sâu sắc hơn về lời giải của bài toán đó.Cách 1: Biến đổi đồng nhất, thay các công thức tổ hợp, đôi khi dùng sai phân, thường xuấtphát từ vế phức tạp rồi dùng một số phép biến đổi để đưa biểu thức về giống vế đơn giản.VD1: Chứng minh các đẳng thức sau:1.111knknC nC n k ( , , )n k N n k 2.22( 1) ( 1)k kn nk k C n n C  ( , ,2 )n k N k n  3.11 11 1 1 12k k kn n nnn C C C     ( , *, )n k N n k (ĐH B 2008)4.2 21n k n kC C  là một số chính phương( , , 2)n k N n k  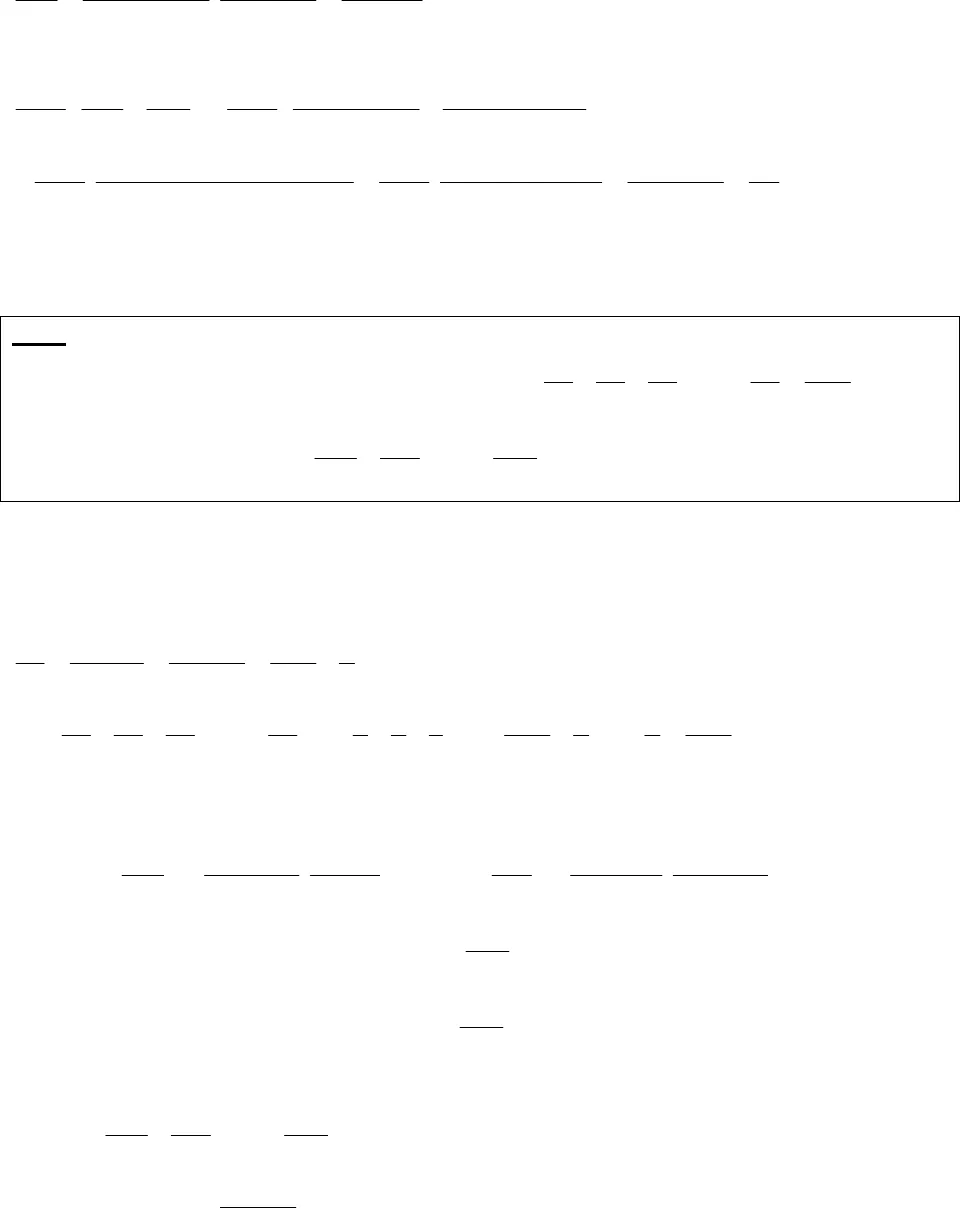2Giải: 1. Dễ dàng nhận thấy ta sẽ xuất phát từ vế trái và ta biến đổi1( 1)! !( )! 1.!( 1)! ! 1knknC n k n k nC k n k n n k      3. Tương tự câu 1, ta cũng sẽ xuất phát từ vế trái là vế phức tạp11 11 1 1 1 !( 1)! ( 1)!( )!2 2 ( 1)! ( 1)!1 !( )!( 1 1) 1 !( )!( 2) !( )! 1. .2 ( 1)! 2 ( 1)! !k kn nknn n k n k k n kn C C n n nn k n k n k k n k n k n k n kn n n n n C                                2,4. Xem như bài tập tự luyện.VD2: (ĐHAN 2001- CĐ 2003)1. Chứng minh với mọi2n và n nguyên thì ta có:2 2 2 22 3 41 1 1 1 1…..nnA A A A n    2. Rút gọn biểu thức:2 311 2 12 3…..nn n nnnn n nC C nCF CC C C    Giải: Bài này minh họa cho ý tưởng sai phân, đó là biến đổi số hạng tổng quát theo hiệu 2 biểuthức rồi thế giá trị và đơn giản từ từ.1. Với1,2,3,…..,n nta có:21 ( 2)! 1 1 1! ( 1) 1nnA n n n n n    Vậy2 2 2 22 3 41 1 1 1 1 1 1 1 1 1 1….. 1 … 12 2 3 1nnA A A A n n n n             2. Cũng với ý tưởng sai phân nhưng ta biến đổi có hơi khác so với câu 11nC n,212 ! ( 1)!2 . 12!( 2)! !nnC n nnC n n  ,323 ! 2!( 2)!3 . 23!( 3)! !nnC n nnC n n  …………………………….11knknkCn kC  …………………………….11nnnnnCCCộng n đẳng thức trên vế theo vế ta được:2 311 2 12 3….. ( 1) ( 2) ….. ( 1) ….. 2 1nn n nnnn n nC C nCF C n n n n kC C C                ( 1)1 2 3 …..2n nn     (theo công thức tính tổng cấp số cộng)3VD3: Chứng minh:1. (ĐHKTCN 1998)1 2 333 3k k k k kn n n n nC C C C C     ( , ,3 )n k N k n  2. (ĐHQGHCM 1997)1 2 3 444 6 4k k k k k kn n n n n nC C C C C C       ( , ,4 )n k N k n  Giải: Bài này minh họa cho HĐT Pascal:1 11k k kn n nC C C  . Công thức này đối với những bạnchưa làm quen thì hơi khó nhớ, có câu “thần chú” sau của thầy mình giúp các bạn dễ nhớ hơn dùnghe nó rất là bình thường: “cùng trệt lầu so le, nâng trệt lấy lầu cao”. Với ý tưởng đó ta sẽ nhómcác số hạng nhằm sử dụng HĐT Pascal:1.     1 2 3 1 1 2 2 33 3 2k k k k k k k k k kn n n n n n n n n nC C C C C C C C C C                  1 2 1 1 2 11 1 1 1 1 1 1 2 2 32k k k k k k k k k kn n n n n n n n n nC C C C C C C C C C                       2. Hoàn toàn tương tự câu 1.VD4: 1. (TTĐTBDCBYTHCM 1998)Cho 2 số nguyên n, m thỏa0 m n . Chứng minh:1 1 1 11 2 1…..m m m m mn n n m mC C C C C         2. Cho, *,n k N n k . Rút gọn:1 2 1…..k k k k kk k k n nS C C C C C       Giải: Ở VD trên là dùng HĐT Pascal theo chiều thuận là gom 2 thành 1, còn ở VD này ta sẽdùng theo chiều ngược tức là tách 1 thành 2.1. Ta có:11 111 2 21 1 1 11 2 11111………. …..1m m mn n nm m mn n nm m m m mn n n m mm m mm m mm mm mC C CC C CC C C C CC C CC C                 2. Hoàn toàn tương tựCách 2: Khai triển lũy thừa nhị thức rồi thay biến bằng giá trị thích hợp.VD1: Chứng minh:1.0 1 2 3….. ( 1) 0n nn n n n nC C C C C      2.0 0 1 1 2 29 9 9 ….. 9 10n n nn n n nC C C C    Giải: 1. Ta thấy vế trái của đẳng thức chứa0nCvànnCđồng thời mỗi hệ số của tổ hợp là 1 nên tasẽ chọn khai triển(1 )nxvà thấy các số hạng đổi dấu nên sẽ chọn1x  .Ta có:0 1 2 2(1 ) …..n n nn n n nx C C x C x C x     (1)Trong (1) thay1x  ta được0 1 2 3….. ( 1) 0n nn n n n nC C C C C      