Giải Toán lớp 10 trang 62, 63 tập 2 Chân trời sáng tạo giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 3 Đường tròn trong mặt phẳng tọa độ thuộc Chương 9 Phương pháp toạ độ trong mặt phẳng.
Bạn đang đọc: Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ
Toán 10 Chân trời sáng tạo trang 62, 63 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 62, 63 Chân trời sáng tạo sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 3: Đường tròn trong mặt phẳng tọa độ mời các bạn cùng theo dõi.
Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ
Giải Toán 10 trang 62, 63 Chân trời sáng tạo – Tập 2
Bài 1 trang 62
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
Gợi ý đáp án
a. Phương trình có dạng với a = 3, b = 4, c = 21
Ta có: 
0″ width=”281″ height=”20″ data-type=”0″ data-latex=”a^{2} + b^{2} – c = 3^{2} + 4^{2} – 21 = 4 > 0″ data-src=”https://tex.vdoc.vn?tex=a%5E%7B2%7D%20%2B%20b%5E%7B2%7D%20-%20c%20%3D%203%5E%7B2%7D%20%2B%204%5E%7B2%7D%20-%2021%20%3D%204%20%3E%200″>. Vậy đây là phương trình đường tròn có tâm I(3; 4) và có bán kính
b. Phương trình có dạng với a = 1, b = -2, c = 2
Ta có: 0″ width=”300″ height=”24″ data-type=”0″ data-latex=”a^{2} + b^{2} – c = 1^{2} + (-2)^{2} – 2 = 3 > 0″ data-src=”https://tex.vdoc.vn?tex=a%5E%7B2%7D%20%2B%20b%5E%7B2%7D%20-%20c%20%3D%201%5E%7B2%7D%20%2B%20(-2)%5E%7B2%7D%20-%202%20%3D%203%20%3E%200″>. Vậy đây là phương trình đường tròn có tâm I(1; -2) và có bán kính
c. Phương trình có dạng với
Ta có: . Vậy đây không phải là phương trình đường tròn.
d. Ta có:
Phương trình có dạng với
Ta có: 0.” width=”361″ height=”41″ data-type=”0″ data-latex=”a^{2} + b^{2} – c = (-frac{1}{4})^{2} + (-frac{1}{4})^{2} + frac{1}{2} = frac{5}{8} > 0.” data-src=”https://tex.vdoc.vn?tex=a%5E%7B2%7D%20%2B%20b%5E%7B2%7D%20-%20c%20%3D%20(-%5Cfrac%7B1%7D%7B4%7D)%5E%7B2%7D%20%2B%20(-%5Cfrac%7B1%7D%7B4%7D)%5E%7B2%7D%20%2B%20%5Cfrac%7B1%7D%7B2%7D%20%3D%20%5Cfrac%7B5%7D%7B8%7D%20%3E%200.”>
Vậy đây là phương trình đường tròn có tâm và bán kính
Bài 2 trang 62
Lập phương trình đường tròn (C) trong các trường hợp sau:
a. (C) có tâm I(1; 5) và có bán kính r = 4;
b. (C) có đường kính MN với M(3; -1) và N(9; 3);
c. (C) có tâm I(2; 1) và tiếp xúc với đường thẳng 5x – 12y + 11 = 0;
d. (C) có tâm A(1; -2) và đi qua điểm B(4; -5).
Gợi ý đáp án
a. Phương trình đường tròn (C) tâm I(1; 5) và bán kính r = 4 là:
b. Tâm I của đường tròn (C) là trung điểm của
Ta có:
Phương trình đường tròn (C) tâm I(6; 1) và bán kính là:
c. Ta có:
Phương tròn đường tròn (C) tâm I(2; 1) và bán kính là:
d. Ta có
Phương trình đường tròn (C) tâm A(1; -2) và bán kính là:
Bài 3 trang 62
Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:
a. M(2; 5), N(1; 2), P(5; 4);
b. A(0; 6), B(7; 7), C(8; 0)
Gợi ý đáp án
a. Phương trình đường tròn có dạng
Thay tọa độ các đỉnh M(2; 5), N(1; 2), P(5, 4) vào phương trình đường tròn, ta được hệ phương trình:
Vậy phương trình đường tròn ngoại tiếp tam giác MNP là:
b. Phương trình đường tròn có dạng
Thay tọa độ các đỉnh A(0; 6), B(7; 7), C(8; 0) vào phương trình đường tròn, ta được hệ phương trình:
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là:
Bài 4 trang 62
Lập phương trình đường tròn tiếp xúc với hai trục Ox, Oy và đi qua điểm A(4; 2).
Gợi ý đáp án
Gọi I(a; b) là tâm đường tròn (C).
Ta có: có tâm I(a; a) và bán kính R = a.
Phương trình đường tròn (C) là:
Ta có nên
hoặc a = 2
Vậy
Bài 5 trang 62
Cho đường tròn (C) có phương trình
a. Chứng tỏ rằng điểm M(4; 6) thuộc đường tròn (C).
b. Viết phương trình tiếp tuyến của (C) tại điểm M(4; 6).
c. Viết phương trình tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0
Gợi ý đáp án
a. Ta có:
Vậy điểm M(4; 6) thuộc đường tròn (C).
b. Đường tròn (C) có tâm I(1; 2) và bán kính
Phương trình tiếp tuyến của (C) tại M(4; 6) là:
c. Tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0 có dạng
Ta có:
Vậy hoặc
Bài 6 trang 62
Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2m như Hình 5. Mặt đường dưới cổng được chia thành hai làn xe ra vào.
a. Viết phương trình mô phỏng cái cổng.
b. Một chiếc xe tải rộng 2,2 m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?
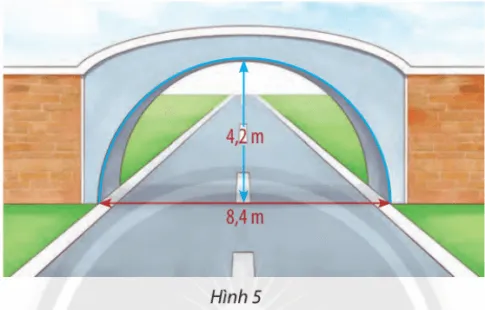
Gợi ý đáp án
a. Chọn hệ tọa độ Oxy như hình vẽ.
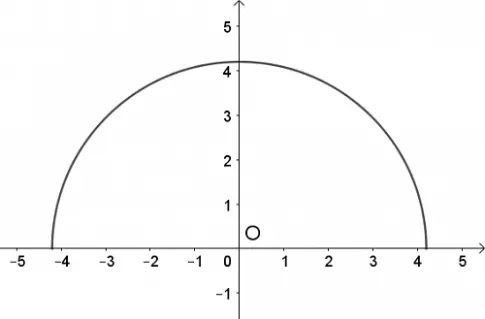
Ta có phương trình đường tròn tâm O(0; 0) bán kính
Rightarrow Phương trình mô phỏng cái cổng là:
b. Thay x = 2,2 vào phương trình đường tròn, ta được 2,6″ width=”269″ height=”37″ data-type=”0″ data-latex=”y = sqrt{17, 64 – 2,2^{2}} approx 3,58 > 2,6″ data-src=”https://tex.vdoc.vn?tex=y%20%3D%20%5Csqrt%7B17%2C%2064%20-%202%2C2%5E%7B2%7D%7D%20%5Capprox%203%2C58%20%3E%202%2C6″>
Vậy xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.
Lý thuyết Đường tròn trong mặt phẳng tọa độ
1. Phương trình đường tròn
Điểm thuộc đường tròn (C), tâm ((a; b), bán kính R khi và chỉ khi
Ta gọi (1) là phương trình của đường tròn (C).
Ví dụ: Tìm tâm và bán kính của đường tròn (C) có phương trình: . Viết phương trình đường tròn (C’) có tâm J(2; – 1) và có bán kinh gấp đôi bán kính đường tròn (C).
Giải
Ta viết phương trình của (C) ở dạng
Vậy (C) có tâm I = (2;- 3) và bán kính R= 4.
Đường tròn (C’) có tâm J(2; – 1) và có bán kinh R’= 2R= 8, nên có phương trình .
Nhận xét: Phương trình (1) tương đương với .
Phương trình là phương trình của một đường tròn (C) khi và chỉ khi
0″ width=”122″ height=”20″ data-type=”0″ data-latex=”{a^2} + {b^2} – c > 0″ data-src=”https://tex.vdoc.vn/?tex=%7Ba%5E2%7D%20%2B%20%7Bb%5E2%7D%20-%20c%20%3E%200″>. Khi đó, (C) có tâm I(a; b) và bán kính R =
Ví dụ: Viết phương trình đường tròn (C) đi qua ba điểm A(2; 0), B(0; 4), C(-7: 3).
Giải
Các đoạn thẳng AB, AC tương ứng có trung điểm là M(1 2), . Đường thẳng trung trực
của đoạn thằng AB đi qua M(1, 2) và có vectơ pháp tuyến
.
Vì cùng phương với
nên
cũng nhận
là vectơ pháp tuyến.
Do đó, phương trình của là
1(x – 1) – 2(y – 2)= 0 hay x – 2y + 3 = 0.
Đường thẳng trung trực của đoạn thẳng AC đi qua
và có vectơ pháp tuyến
.
Vì A€(-9; 3) cùng phương với n; (3 – 1) nên Az cũng nhận n; (3 – 1) là vectơ pháp tuyến.
Do đó, phương trinh của là
hay 3x – y + 9 = 0
Tâm I của đường tròn (C) cách đều ba điểm A, B, C nên I là giao điểm của và
.
Vậy toạ độ của I là nghiệm của hệ phương trình
Suy ra I(-3; 0). Đường tròn (C) có bán kính là IA = 5. Vậy phương trình của (C) là
