Toán 10 Bài 6 Kết nối tri thức trang 42, 43 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi Luyện tập và 7 bài tập trong SGK bài Hệ thức lượng trong tam giác.
Bạn đang đọc: Toán 10 Bài 6: Hệ thức lượng trong tam giác
Giải Toán 10 Kết nối tri thức bài 6 trang 37 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 bài 6 Kết nối tri thức là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là nội dung chi tiết giải Toán 10 Bài 6 Hệ thức lượng trong tam giác mời các bạn cùng theo dõi.
Toán 10 Bài 6: Hệ thức lượng trong tam giác
Luyện tập Toán 10 Bài 6 Kết nối tri thức
Luyện tập 1
Cho tam giác ABC, có AB = 5, AC = 8 và góc A = 45°. Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Gợi ý đáp án
Hình vẽ minh họa:
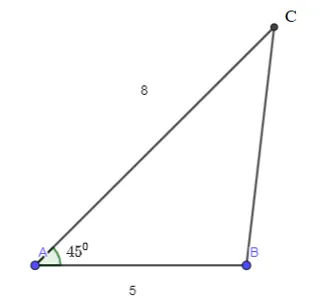
Xét tam giác ABC
Theo định lí cosin, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
BC2 = 52 + 82 – 2.5.8.cos450
BC ≈ 5,7 cm
Ta có:
Luyện tập 2
Cho tam giác ABC có b = 8; c = 5 và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài các cạnh còn lại của tam giác.
Gợi ý đáp án
Hình vẽ minh họa:
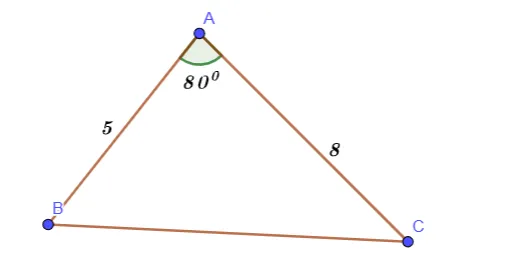
Xét tam giác ABC ta có:
Theo định lý Cos, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 52 + 82 – 2.5.8.cos800 ≈ 75
BC ≈ 8,7
Áp dụng định lý sin trong tam giác ta có:
=>
Vậy BC = 8,7;
Luyện tập 3
Giải tam giác ABC biết a = 32, c = 45 và
Gợi ý đáp án
Hình vẽ minh họa:
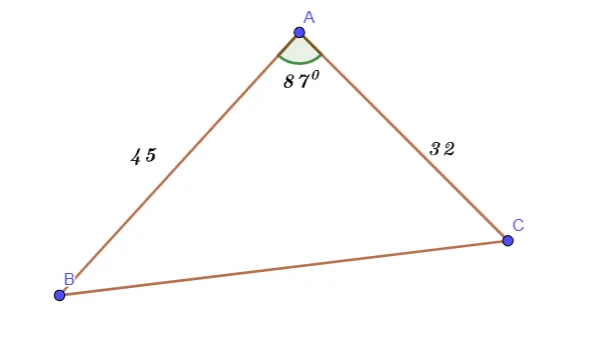
Xét tam giác ABC ta có:
Theo định lý Cos, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 322 + 452 – 2.32.45.cos870 ≈ 2898,27
BC ≈ 53,84
Áp dụng định lý sin trong tam giác ta có:
=>
Vậy BC = 53,84;
Giải Toán 10 Kết nối tri thức trang 42, 43 Tập 1
Bài 3.5 trang 42
Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Gợi ý đáp án
Từ định lí cosin ta suy ra
Tam giác ABC có nửa chu vi là:
Theo công thức Herong ta có:
Lại có:
Vậy
Bài 3.6 trang 42
Cho tam giác ABC có Tính R,b,c.
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC ta có:
Mà
Mặt khác:
Từ định lí sin ta suy ra:
Vậy .
Bài 3.7 trang 42
Giải tam giác ABC và tính diện tích của tam giác đó, biết
Gợi ý đáp án
Ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
Mà
Diện tích tam giác ABC là
Vậy
Bài 3.8 trang 42
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S{70^o}E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Gợi ý đáp án
Ta có sơ đồ đường đi như sau:
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).
Ban đầu tàu di chuyển theo hướng nên
. Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay c = 105.
Quãng đường tàu trôi tự do là:
8.2 = 16 (km) hay a = 16.
Áp dụng định lí cosin cho tam giác ABC ta có:
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 110,23 km.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là
Áp dụng định lí sin cho tam giác ABC ta có:
Mà
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là
Bài 3.9 trang 43
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là và
so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
Gợi ý đáp án
a) Tính các góc của tam giác ABC.
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có:
Xét tam giác ABH, vuông tại H ta có:
Từ (1) và (2), suy ra:
Vậy ba góc của tam giác ABC lần lượt là:
b) Tính chiều cao của tòa nhà.
Áp dụng định lý sin cho tam giác ABC, ta được:
Mà:
Xét tam giác ABH, vuông tại H ta có:
Mà:
Vậy chiều cao của tòa nhà là:
Bài 3.10 trang 43
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một các xác định bề rộng của hòn đảo (theo chiều ta ngắm được).
Gợi ý đáp án
Bước 1:
Đánh dấu vị trí quan sát tại điểm A, chiều rộng của hòn đảo kí hiệu là đoạn BC.
Gọi H là hình chiếu của A trên BC.
Trên tia đối của tia AH, lấy điểm M, ghi lại khoảng cách AM = a.
Bước 2:
Tại A, quan sát để xác định các góc
Tiếp tục quan sát tại M, xác định góc
Bước 3: Giải tam giác AMC, tính AC.
Áp dụng định định lí sin trong tam giác AMC ta có:
Bước 4:
Áp dụng định lí sin cho tam giác ABC ta có:
Bài 3.11 trang 43
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
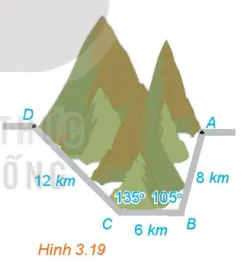
Gợi ý đáp án
Bước 1:
Áp dụng định lí cos trong tam giác ABC ta có:
Bước 2:
Lại có: Theo định lí sin thì
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: 12 + 6 + 8 – 16,6 = 9,4 (km)
Lý thuyết Hệ thức lượng trong tam giác
1. Định lý cosin
Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
Hệ quả của định lí cosin:
Áp dụng: Tính độ dài đường trung tuyến của tam giác:
Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi m_a,m_b và m_c là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác. Ta có
2. Định lí sin
Định lí: Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là
với R là bán kính đường tròn ngoại tiếp tam giác

