Giải Toán 10 Bài 7: Các khái niệm mở đầu sách Kết nối tri thức với cuộc sống giúp các em học sinh lớp 10 có thêm nhiều tư liệu tham khảo để giải các câu hỏi phần bài tập trang 50 tập 1 được nhanh chóng và dễ dàng hơn.
Bạn đang đọc: Toán 10 Bài 7: Các khái niệm mở đầu
Giải Toán 10 trang 50 Tập 1 sách Kết nối tri thức giúp các em luyện tập, giải các bài tập về vecto. Giải Toán lớp 10 Bài 7 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết bài Giải Toán 10 trang 50 sách Kết nối tri thức với cuộc sống Tập 1, mời các bạn tải tại đây.
Giải Toán 10 Bài 7: Các khái niệm mở đầu tập 1
Lý thuyết Các khái niệm mở đầu
Hai Vectơ cùng phương, cùng hướng, bằng nhau
+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Ví dụ: Giá của vecto là đường thẳng CD
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Ví dụ:
Ba vecto cùng phương.
Trong đó 2 vecto cùng hướng, còn 2 vecto
ngược hướng.
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
* Chú ý:
– Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.
– Vecto cùng phương, cùng hướng với mọi vecto.
– Với mỗi điểm O và vecto cho trước, có duy nhất điểm A sao cho
* Nhận xét:
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi và
cùng phương.
+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi và
cùng hướng.
Giải Toán 10 Kết nối tri thức trang 50 Tập 1
Bài 4.1 trang 50
Cho 3 vectơ đều khác
. Những khẳng định nào sau đây là đúng?
a) đều cùng hướng với vectơ
b) Nếu không cùng hướng với
thì
ngược hướng với
c) Nếu và
đều cùng phương với
thì
và
cùng phương.
d) Nếu và
đều cùng hướng với
thì
và
cùng hướng.
Gợi ý đáp án
a) Đúng vì vectơ cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).

c) Đúng.
và
đều cùng phương với
thì a // c và b // c do đó a // b tức là
và
cùng phương.
d) Đúng.
và
đều cùng hướng với
thì
và
cùng phương , cùng chiều đo đó cùng hướng.
Bài 4.2 trang 50
Trong Hình 4.12, hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.
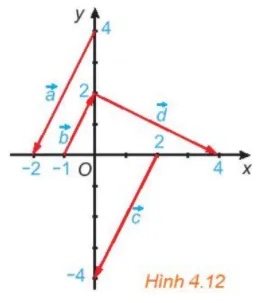
Gợi ý đáp án
Các vecto cùng phương là:
Trong đó cặp vecto cùng hướng, cặp
và cặp vecto
ngược hướng.
Bài 4.3 trang 50
Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi
Gợi ý đáp án
Tứ giác ABCD là một hình bình hành
Hai vecto
và
cùng hướng và AD = BC.
. (đpcm)
Bài 4.4 trang 50
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác . Hãy chỉ ra tập hợp S gồm tất cả các vceto khác
có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Gợi ý đáp án

Tập hợp S là: ;
;
Các nhóm trong S là:
Bài 4.5 trang 50
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn với vecto Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Gợi ý đáp án
Dễ thấy: OA // MN do đó cùng phương.
Hơn nữa, cùng hướng và MN = 3 OA.
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.

