Bài tập cuối chương 3 Toán 10 Chân trời sáng tạo giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các bài tập tự luận từ câu 1 đến câu 7 trong SGK chương Hàm số bậc hai và đồ thị.
Bạn đang đọc: Toán 10 Bài tập cuối chương III – Chân trời sáng tạo
Giải Toán 10 Chân trời sáng tạo trang 59 Tập 1 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa. Giải Bài tập cuối chương 3 Toán 10 Chân trời sáng tạo là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Toán 10 Bài tập cuối chương III: Hàm số bậc hai và đồ thị
Giải Toán 10 trang 59 Chân trời sáng tạo – Tập 1
Bài 1 trang 59
Tìm tập xác định của các hàm số sau:
Gợi ý đáp án
a) Biểu thức có nghĩa với mọi
Vậy tập xác định của hàm số này là
b) Biểu thức f(x) có nghĩa khi và chỉ khi , tức là với mọi
Vậy tập xác định của hàm số này là
c) Biểu thức f(x) có nghĩa khi và chỉ khi có nghĩa, tức là khi x ne 0,
Vậy tập xác định của hàm số này là
Bài 2 trang 59
Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:
a) y = (1 – 3m)x2 + 3;
b) y = (4m – 1)(x – 7)2;
c) y = 2(x2 + 1) + 11 – m.
Gợi ý đáp án
a) Để hàm số là hàm số bậc hai thì:
tức là
Vây thì hàm số đã cho là hàm số bậc hai.
b) Để hàm số là hàm số bậc hai thì:
tức là m = 2.
Khi đó
Vậy m = 2 thì hàm số đã cho là hàm số bậc hai
Bài 3 trang 59
a) y = x2 – 4x + 3;
b) y = – x2 – 4x + 5;
c) y = x2 – 4x + 5;
d) y = -x2 – 2x – 1.
Gợi ý đáp án
a) y = x2 – 4x + 3
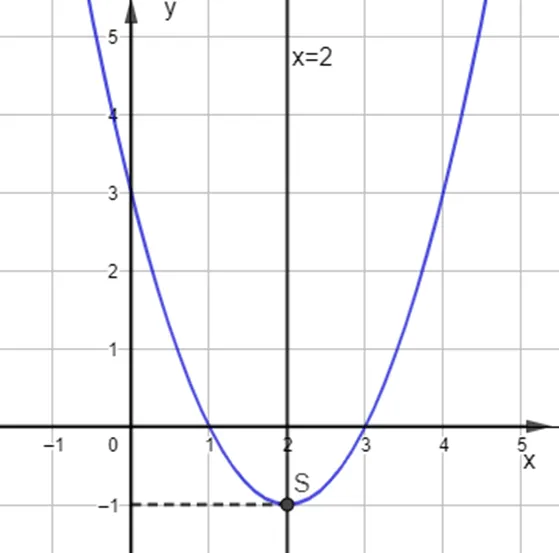
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = x2 – 4x + 3 là một parabol (P1):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = -1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a > 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ngoài ra, phương trình x2 – 4x + 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta có đồ thị sau:
b) y = – x2 – 4x + 5:
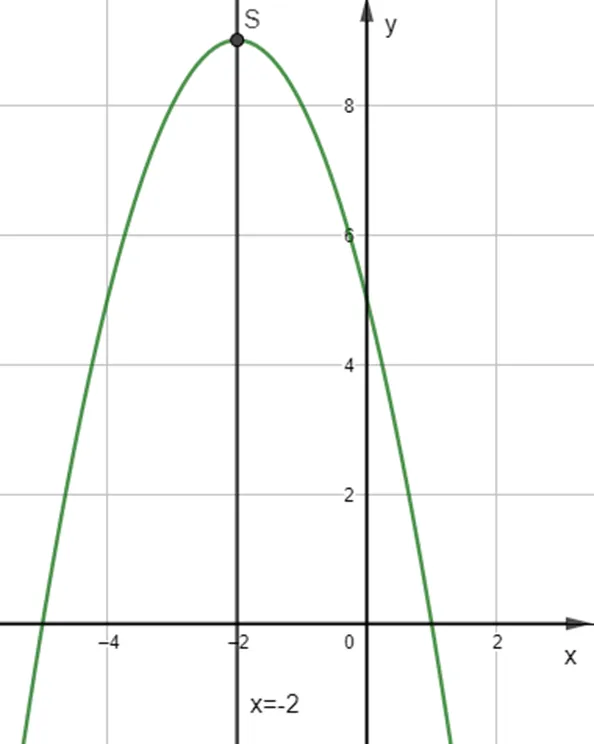
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = – x2 – 4x + 5 là một parabol:
– Có đỉnh S với hoành độ xS = -2, tung độ yS = 9;
– Có trục đối xứng là đường thẳng x = -2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a
– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ngoài ra, phương trình – x2 – 4x + 5 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = -5 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (1; 0) và (-5; 0).
Ta có đồ thị sau:
c) y = x2 – 4x + 5:
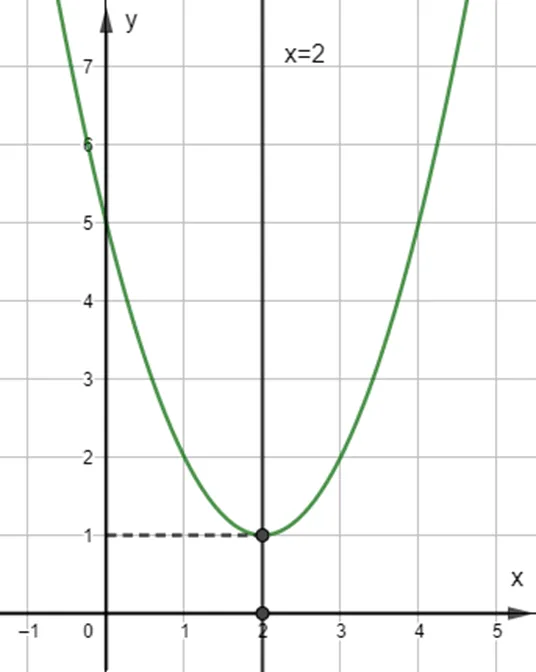
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = x2 – 4x + 5 là một parabol:
– Có đỉnh S với hoành độ xS = 2, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a > 0;
– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ngoài ra, phương trình x2 – 4x + 5 = 0 vô nghiệm nên đồ thị hàm số không cắt trục hoành.
Ta có đồ thị sau:
d) y = -x2 – 2x – 1.
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = -x2 – 2x – 1 là một parabol:
– Có đỉnh S với hoành độ xS = -1, tung độ yS = 0;
– Có trục đối xứng là đường thẳng x = -1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a
– Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ngoài ra, phương trình -x2 – 2x – 1 = 0 có nghiệm x = – 1 nên đồ thị hàm số cắt trục hoành tại điểm có tọa độ (-1; 0).

Bài 4 trang 59
Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h.
a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số.
b) Vẽ đồ thị biểu diễn hàm số s theo t.
Gợi ý đáp án
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = giờ
Nếu thì quãng đường s mà người đó đi được là:
Nếu (phút) thì quãng đường s mà người đó đi được là: 42.1,5 = 63(km)
Nếu (phút) thì quãng đường s mà người đó đi được là:
Như vậy hàm số tính quãng đường s (km) sau t phút là:
b)
Với thì s = 0,7t
Trên đoạn [0;90] ta vẽ đường thẳng s = 0,7t
Với thì s = 63(km)
Trên nửa khoảng (90;105] ta vẽ đường thẳng s = 63
Với (phút) thì s = 0,5t + 10,5.(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng s = 0,5t + 10,5.
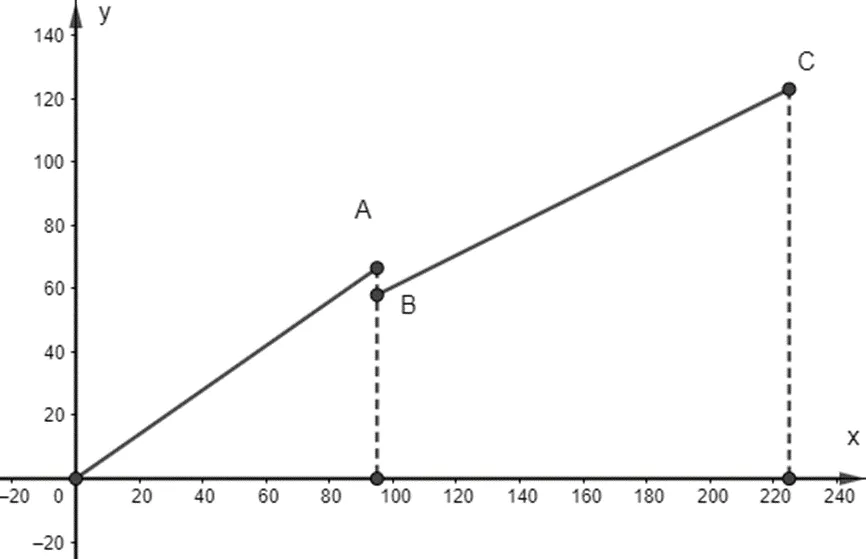
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.
Bài 5 trang 59
Biết rằng hàm số giảm trên khoảng
, tăng trên khoảng
và có tập giá trị là
. Xác định giá trị của m và n.
Gợi ý đáp án
Đỉnh S có tọa độ:
Vì hàm số bậc hai có a = 2 > 0 nên ta có bảng biến thiên sau:
Hàm số đạt giá trị nhỏ nhất bằng
Hàm số giảm trên và tăng trên
Theo giả thiết, ta có:
Hàm số giảm trên khoảng
Tương tự hàm số tăng trên khoảng
Do đó: hay m = – 4
Lại có: Tập giá trị là Giá trị nhỏ nhất của hàm số bằng 9.
Vậy m = – 4,n = 3.
Bài 6 trang 59
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhày bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.
Gợi ý đáp án
Gọi là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Chọn hệ trục tọa độ Oxy như hình dưới:
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (48; 46,2) và B (117+48; 0) = (165; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
Giải hệ phương trình
Vậy
Đỉnh S có tọa độ là
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: 1 + 56 + 43 = 100(m)
Vậy chiều dài của sợi dây đó là:
Bài 7 trang 59
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúngvị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí nào? Biết rằng nếu chọn gốc toạ độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì toạ độ của hàng cứu trợ được cho bởi hệ sau:
Trong đó, là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
Gợi ý đáp án
Gắn hệ trục tọa độ Oxy như hình dưới:
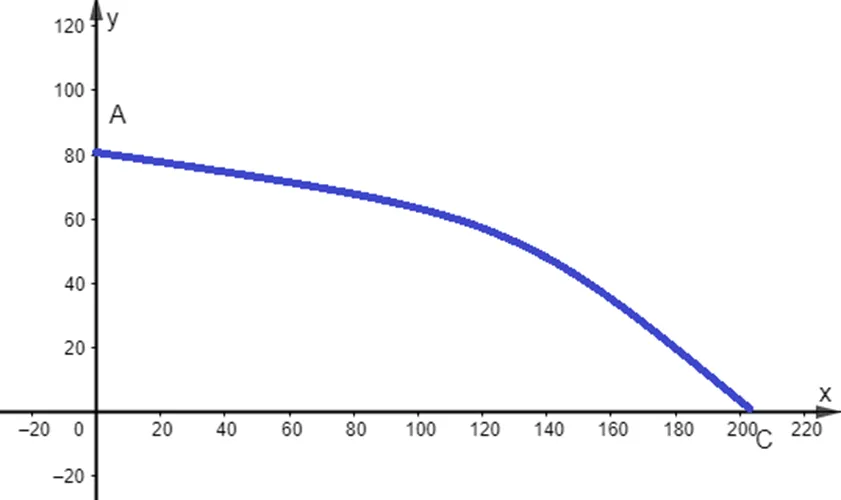
Gọi A vị trí hàng rơi xuống, khi đó . Ta có, tọa độ của A thỏa mãn:
Mà
Do đó hay khoảng cách giữa máy bay và thùng hàng cứu trợ là 200m.
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn thì máy bay cần thả hàng khi cách điểm đó 200m.
Lý thuyết Hàm số bậc hai và đồ thị
1. Hàm số bậc hai
+ Định nghĩa:
Hàm số bậc hai biến x là hàm số cho bởi công thức dạng với
+ Tập xác định:
2. Đồ thị hàm số bậc hai
+) Đồ thị hàm số bậc hai là một parabol (P):
– Đỉnh
– Trục đối xứng: đường thẳng
– Bề lõm: quay lên trên nếu a > 0, quay xuống dưới nếu a
– Cắt Oy tại điểm (0;c)
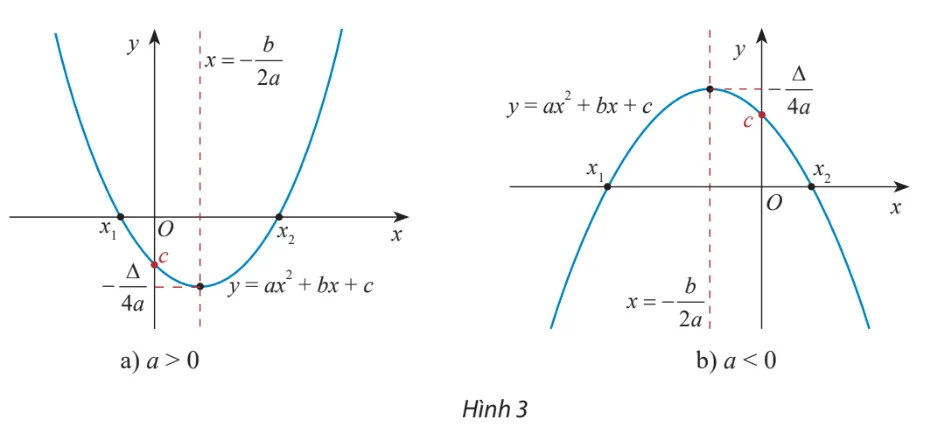
* Chú ý: Nếu PT có hai nghiệm
thì đồ thị hàm số
cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.
+) Vẽ đồ thị
1) Xác định đỉnh
2) Vẽ trục đối xứng
3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).
Xác định (là điểm đối xứng với A qua d)