Toán lớp 11 trang 88 Cánh diều tập 2 là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.
Bạn đang đọc: Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Giải Toán 11 Cánh diều Bài 2 Đường thẳng vuông góc với mặt phẳng được biên soạn đầy đủ, chi tiết trả lời các câu hỏi trang 80, 81,82, 83, 84, 85, 86, 87, 88. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 trang 88 Cánh diều Tập 2, mời các bạn cùng theo dõi tại đây.
Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
Giải Toán 11 trang 88 Cánh diều – Tập 2
Bài 1
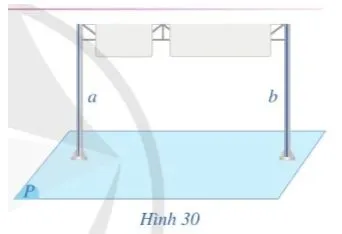
Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng.
Gợi ý đáp án
• Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
• Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Bài 2
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC).
b) Giả sử BC ⊥ SA, CA ⊥ SB. Chứng minh rằng H là trực tâm của tam giác ABC và AB ⊥ SC.
Gợi ý đáp án
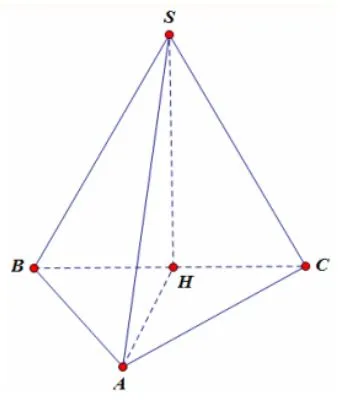
a) Để xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC), ta có thể vẽ đường thẳng vuông góc từ điểm S đến mặt phẳng (ABC), kết hợp với việc vẽ các đường thẳng từ A, B, C vuông góc với mặt phẳng (ABC) để tìm hình chiếu của các đường thẳng đó. Hình chiếu của SA, SB, SC lần lượt là AD, BE, CF
b) Vì BC ⊥ SA và CA ⊥ SB, nên BC và CA lần lượt là các đường vuông góc với SA và SB. Do đó, ta có:
- SA ⊥ (ABC) ⇒ SH ⊥ BC và SK ⊥ AB (trong đó H và K lần lượt là hình chiếu của S xuống BC và AB)
- SB ⊥ (ABC) ⇒ SJ ⊥ AC và SL ⊥ AB (trong đó J và L lần lượt là hình chiếu của S xuống AC và AB)
- SC ⊥ (ABC) ⇒ SM ⊥ AB và SN ⊥ AC (trong đó M và N lần lượt là hình chiếu của S xuống AB và AC)
Khi đó, ta thấy rằng tam giác ABC có ba đường cao HN, KM và LJ, nên H là trực tâm của tam giác ABC (vì trực tâm là điểm giao điểm của ba đường cao của tam giác).
Bên cạnh đó, ta có AB ⊥ SL (vì AB vuông góc với mặt phẳng (ABC), SL vuông góc với AB), và từ đó suy ra AB ⊥ SC (vì SL là hình chiếu của SC xuống AB). Vậy AB ⊥ SC, như cần chứng minh.
Bài 3
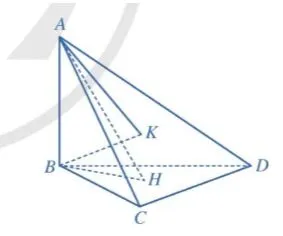
Cho tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của tam giác BCD, ACD. Chứng minh rằng:
a) CD ⊥ (ABH)
b) CD ⊥ (ABK)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
Gợi ý đáp án
a) Vì AB ⊥ (BCD)
=> AB ⊥ CD (1)
Có H là trực tâm của tam giác BCD => BH ⊥ CD (2)
Từ (1) và (2) => CD ⊥ (ABH)
b) Vì AB ⊥ (BCD)
=> AB ⊥ CD (1)
Có K là trực tâm của tam giác ACD => AK ⊥ CD (2)
Từ (1) và (2) => CD ⊥ (ABK)
Bài 4
Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng
a) SA ⊥ AD
b) SC ⊥ CD
Gợi ý đáp án
a) Chứng minh SA ⊥ AD
Gọi M là trung điểm của AB
=> HM // CD (vì AB và CD là hai đường chéo của hình bình hành).
Có SA vuông góc với mặt phẳng (ABCD) và SM vuông góc với HM. Vì SM song song với CD, nên SA cũng vuông góc với CD. Do đó, ta có SA ⊥ AD.
b) Chứng minh SC ⊥ CD
Chứng minh tương tự, gọi N là trung điểm của CD. Ta có HN song song với AB. Theo tính chất đường thẳng vuông góc với mặt phẳng, ta biết rằng SC vuông góc với mặt phẳng (ABCD) và SN vuông góc với HN. Vì SN song song với AB, nên SC cũng vuông góc với AB. Do đó, ta có SC ⊥ CD.
Bài 5
Cho hình chóp S.ABCD có SA ⊥ (ABC), BC ⊥ AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông.
Gợi ý đáp án
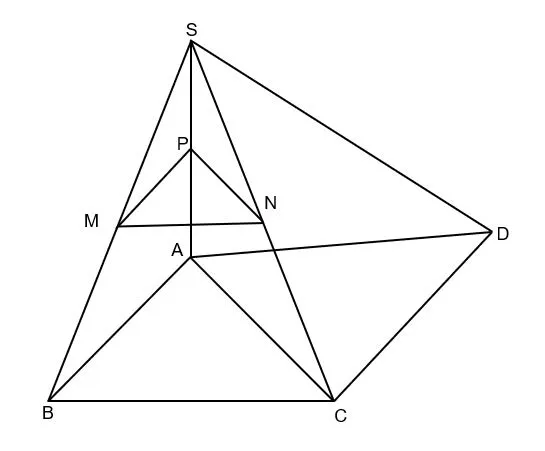
Có SA ⊥ (ABC) => SA ⊥ BC
mà BC ⊥ AB
=> BC ⊥ (SAB)
=> BC ⊥ MP (1)
Xét tam giác SBC có M, N lần lượt là trung điểm của SB, SC
=> MN là đường trung bình của tam giác SBC
=> MN // BC (2)
Từ (1) và (2)
=> MN ⊥ MP
=> tam giác MNP là tam giác vuông tại M

