Toán lớp 11 tập 1 trang 100, 101, 102, 103, 104, 105, 106 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.
Bạn đang đọc: Toán 11 Bài 2: Hai đường thẳng song song
Giải Toán 11 Chân trời sáng tạo bài 2 Hai đường thẳng song song được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 105, 106. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 1 bài 2 Hai đường thẳng song song Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.
Toán 11 Bài 2: Hai đường thẳng song song
I. Toán lớp 11 tập 1 trang 105, 106
Bài 1
Cho hai đường thẳng song song a và b. Mệnh đề sau đây là đúng hay sai?
a) Một đường thẳng c cắt a thì cũng cắt b
b) Một đường thẳng c chéo a thì cũng chéo b
Bài làm
2 mệnh đề trên đều sai
Bài 2
Cho hình chóp S.ABC và điểm M thuộc miền trong tam giác ABC (Hình 17). Qua M, vẽ đường thẳng d song song với SA, cắt (SBC) tại N. Trên hình vẽ, hãy chỉ rõ vị trí của điểm N và xác định giao tuyến của hai mặt phẳng (SAC) và (CMN).
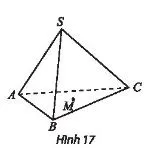
Bài làm
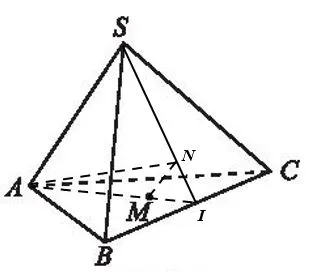
Gọi I là giao điểm của AM và BC. Trong mặt phẳng (SAI), kẻ đường thẳng d song sóng SA cắt SI tại N
Giao tuyến của hai mặt phẳng (SAC) và (CMN) là đường thẳng đi qua C và song song với SA và MN
Bài 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của hai mặt phẳng (SCD) và (SAB)
b) Lấy một điểm M trên đoạn SA (M khác S và A), mặt phẳng (BCM) cắt SD tại N. Tứ giác CBMN là hình gì?
Bài làm
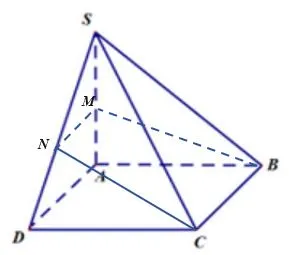
a) Giao tuyến của hai mặt phẳng (SCD) và (SAB) là đường thẳng đi qua S và song song với AB và CD
b) Giao tuyến của (BCM) với (SAD) là đường thẳng MN song song với BC
Do đó CBMN là hình thang
Bài 4
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm của SD. Hai mặt phẳng (IAC) và (SBC) cắt nhau theo giao tuyến Cx. Chứng minh rằng Cx//SB.
Bài làm
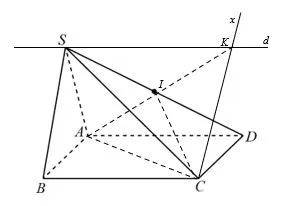
Mặt phẳng (SBC) và (SAD) giao nhau tại đường thẳng d đi qua S và song song với BC
Trong mặt phẳng (SAD), kéo dài AI cắt d tại K.
AI ⊂ (AIC) nên K ∈ (ACI)
Ta có C và K là 2 điểm chung của hai mặt phẳng (SBC) và (CIA) nên CK là giao tuyến của hai mặt phẳng (SBC) và (CIA)
Trong mặt phẳng (SADK) ta có AD//SK, I là trung điểm của SD nên AD = SK. Mà AB = BD. Suy ra SK = BC
Ta có SK//BC, SK = BC nên SBCK là hình bình hành.
Suy ra CK//SB. Hay Cx//SB
Bài 5
Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng (ICD) cắt SA, SB lần lượt tại M, N.
a) Hãy nói cách xác định hai điểm M và N. Cho AB = a. Tính MN theo a
b) Trong mặt phẳng (CDMN), gọi K là giao điểm của CN và DM. Chứng minh SK//BC//AD
Bài làm
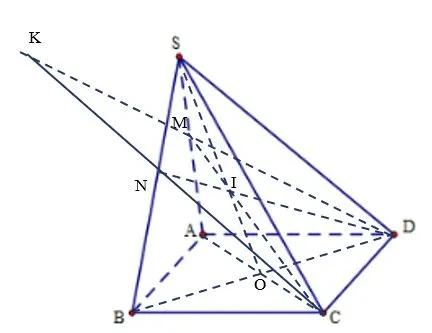
a) Trong mặt phẳng (SAC), gọi M là giao của CI và SA. CI ⊂ (ICD) nên M ∈ (ICD)
Trong mặt phẳng (SBD), gọi N là giao của DI và SB. DI ⊂ (ICD) nên N ∈ (ICD)
Ta có MN là giao của của (ICD) và (SAB). Mà AB//CD nên MN//CD
Theo định lý Menelaus, trong tam giác SOA, ta có: .
.
= 1
Hay . 2 . 1 = 1. Suy ra:
=
Nên
=
Ta có MN//AB nên =
Vậy MN = a
b) K ∈ CN; CN ⊂ (SBC) nên K ∈ (SBC)
K ∈ DM; DM ⊂ (SAD) nên K ∈ (SAD)
Ta có S và K là hai điểm chung của hai mặt phẳng (SAD) và (SBC) nên SK là giao tuyến của hai mặt phẳng (SAD) và (SBC).
Mà AD//BC nên SK//BC//AD
Bài 6
Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các đường thẳng song song trong thực tế
Bài làm
Hình a: Các dây điện song song với nhau
Hình b: Các mép của viên gạch lát song song với nhau
Hình c: Các mép của bậc thang song song với nhau
Hình d: Các mép của phím đàn song song với nhau
Hình e: Các mép của từng ngăn kệ song song với nhau
Hình g: Các mép của viên gạch song song với nhau
Một số ví dụ khác về đường thẳng song song: Các gáy của quyền sách trong chồng sách, Các mép của chân bàn thẳng đứng,…
II. Luyện tập Hai đường thẳng song song
Bài trắc nghiệm số: 4410

