Giải Toán lớp 11 trang 57, 58 tập 1 Cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK Bài tập cuối chương II.
Bạn đang đọc: Toán 11 Bài tập cuối chương II
Toán 11 Cánh diều tập 1 trang 57, 58 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 11. Giải Toán lớp 11 trang 57, 58 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 11 Bài tập cuối chương II trang 57, 58
Bài tập 1 trang 57
Cho dãy số () được xác định bởi:
và
với mọi
. Số hạng thứ năm của dãy số (
) là:
A.
B.
C.
D.
Trả lời: Chọn đáp án A
Bài tập 2 trang 57
Trong các dãy số sau, dãy số nào là cấp số cộng?
A.
B.
C.
D.
Trả lời: Chọn đáp án A
Bài tập 3 trang 57
Cho cấp số cộng () có số hạng đầu
, công sai
. Công thức của số hạng tổng quát
là:
A.
B.
C.
D.
Trả lời: Chọn đáp án D
Bài tập 4 trang 57
Tổng 100 số tự nhiên lẻ đầu tiên tính từ 1 là:
A. 10 000
B. 10 100
C. 20 000
D. 20 200
Trả lời: Chọn đáp án A
Bài tập 5 trang 57
Trong các dãy số () cho bằng phương pháp truy hồi sau, dãy số nào là cấp số nhân?
A. Dãy số () được xác định bởi:
và
với mọi
B. Dãy số () được xác định bởi:
và
với mọi
C. Dãy số () được xác định bởi:
và
với mọi
D. Dãy số () được xác định bởi:
và
với mọi
Trả lời: Chọn đáp án D
Bài tập 6 trang 57
Cho cấp số nhân () có
, công bội
. Khi đó
là số hạng thứ:
A. 2016
B. 2017
C. 2018
D. 2019
Trả lời: Chọn đáp án C
Bài tập 7 trang 57
Trong các dãy số () sau đây, dãy số nào là dãy số tăng?
A.
B.
C.
D.
Trả lời: Chọn đáp án D
Bài tập 8 trang 58
Xét tính tăng, giảm và bị chặn của mỗi dãy số () sau, biết số hạng tổng quát:
a)
b)
c)
Trả lời:
a) Dãy số là dãy số tăng và bị chặn dưới vì
0″ data-type=”2″ data-latex=”frac{n^{2}}{n+1}> 0″ data-src=”https://tex.vdoc.vn/?tex=%5Cfrac%7Bn%5E%7B2%7D%7D%7Bn%2B1%7D%3E%200″>.
b) Dãy số là dãy số giảm và bị chặn dưới vì
.
c) Dãy số là dãy số không tăng không giảm và không bị chặn.
Bài tập 9 trang 58
Cho cấp số cộng (). Tìm số hạng đầu
, công sai
trong mỗi trường hợp sau:
a) và
b) và
.
Trả lời:
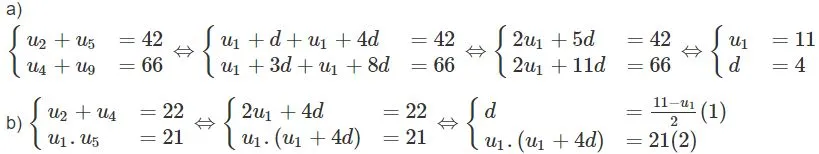
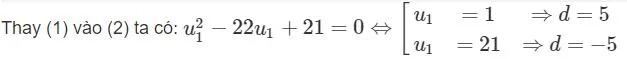
Bài tập 10 trang 58
Cho cấp số nhân ().Tìm số hạng đầu
, công bội
trong mỗi trường hợp sau:
a) và
b) và
.
Trả lời:
a) Ta có:
Chia ta có:
Thay vào (1) ta có:
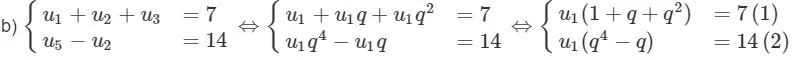
Chia ta có:
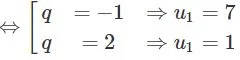
Bài tập 11 trang 58
Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.
Trả lời:
Ta có:
Mà:
Vì:
Bài tập 12 trang 58
Người ta trồng cây theo các hàng ngang với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây, … ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4 950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
Trả lời:
Ta có:
Vậy có 99 hàng cây được trồng theo cách trên.
Bài tập 13 trang 58
Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay bên dưới. Biết mặt đáy tháp có diện tích là . Tính diện tích của mặt sàn tầng trên cùng của tháp theo đơn vị mét vuông.
Trả lời:
Ta có:
Do đó: (mét vuông).
Bài tập 14 trang 58
Một khay nước có nhiệt độ được đặt vào ngăn đá của tủ lạnh. Biết sau mỗi giờ, nhiệt độ của nước giảm 20%. Tính nhiệt độ của khay nước đó sau 6 giờ theo đơn vị độ C.
Trả lời:
Nhiệt độ của khay nước đó sau 6 giờ là: (độ C).
Bài tập 15 trang 58
Cho hình vuông có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
(Hình 4). Từ hình vuông
lại làm tiếp tục như trên để có hình vuông
. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông
Gọi
là độ dài cạnh hình vuông
. Chứng minh rằng dãy số (
) là cấp số nhân.
Gợi ý đáp án
Hình vuông C1 có độ dài cạnh u1 = 4
Hình vuông C2 có độ dài cạnh:
Hình vuông C3 có độ dài cạnh là:
Hình vuông C4 có độ dài cạnh là:
…
Ta có:
Do đó, dãy số trên là một cấp số nhân với số hang đầu u1 = 4 công bội .
Bài tập 16 trang 58
: Ông An vay ngân hàng 1 tỉ đồng với lãi suất 12%/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?
Gợi ý đáp án
Giả sử An là số tiền ông An còn nợ ngân hàng sau mỗi tháng.
1 năm = 12 tháng, do đó lãi suất mỗi tháng là 1%.
1 tỷ = 1 000 (triệu đồng)
Suy ra số tiền lãi 1 tháng là: 1 000 . 1% = 10 (triệu đồng)
Ta có:
A0 = 1 000 (triệu đồng)
A1 = 1 000 + 1 000 . 10% – a = 1 000 + 10 – a (triệu đồng)
A2 = 1 000 + 10 – a + 10 – a = 1 000 + 2.10 – 2a (triệu đồng)
A3 = 1 000 + 2.10 – 2a + 10 – a = 1 000 + 3.10 – 3a (triệu đồng)
…
An = 1 000 + n.10 – n.a (triệu đồng)
Do 2 năm ông An trả hết nợ tức là A24 = 0
=> 1 000 + 24.10 – 24 . a = 0
=> 1 240 – 24a = 0
=> a ≈ 51,67 (triệu đồng)
Vậy mỗi tháng ông An phải trả 51,67 triệu đồng.
