Giải Toán lớp 6 Bài 10: Số nguyên tố bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 1 Kết nối tri thức trang 38, 39, 40, 41, 42. Với lời giải chi tiết, trình bày khoa học, được biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn.
Bạn đang đọc: Toán 6 Bài 10: Số nguyên tố
Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 10 Chương II: Tính chia hết trong tập hợp các số tự nhiên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 6 bài 10: Số nguyên tố Kết nối tri thức với cuộc sống
Giải Toán 6 Kết nối tri thức với cuộc sống Mở đầu
Mẹ mua một bó hoa có 11 bông hoa hồng. Bạn Mai giúp mẹ cắm các bông hoa này vào các lọ nhỏ sao cho số bông hoa trong mỗi lọ nhỏ là như nhau. Mai nhận thấy không thể cắm đều số bông hoa này vào các lọ hoa (mỗi lọ có nhiều hơn một bông) cho dù số lọ hoa là 2; 3; 4; 5;… Nhưng nếu bỏ ra một bông còn 10 bông thì lại cắm đều được vào 2 lọ, mỗi lọ co 5 bông hoa.
Vậy số 11 và số 10 có gì khác nhau, điều này có liên quan gì đến số các ước của chúng không?
Gợi ý đáp án:
Ta có: Các ước của 11 là: 1; 11
Các ước của 10 là: 1; 2; 5; 10
Do đó ta thấy số 11 chỉ có hai ước là 1 và chính nó, còn số 10 thì có nhiều hơn 2 ước (cụ thể ở đây là 4 ước số tự nhiên).
Qua bài học này, ta sẽ biết được hai số 11 và 10 là khác nhau. Số 11 gọi là số nguyên tố và số 10 gọi là hợp số.
Giải Toán 6 Kết nối tri thức với cuộc sống Bài 10 – Hoạt động
Hoạt động 1
Tìm các ước và số ước của các số trong bảng 2.1
| Số | Các ước | Số ước |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | 1, 2, 5, 10 | 4 |
| 11 | 1, 11 | 2 |
Gợi ý đáp án:
| Số | Các ước | Số ước |
| 2 | 1, 2 | 2 |
| 3 | 1, 3 | 2 |
| 4 | 1, 2, 4 | 3 |
| 5 | 1, 5 | 2 |
| 6 | 1, 2, 3, 6 | 4 |
| 7 | 1, 7 | 2 |
| 8 | 1, 2, 4, 8 | 4 |
| 9 | 1, 3, 9 | 3 |
| 10 | 1, 2, 5, 10 | 4 |
| 11 | 1, 11 | 2 |
Hoạt động 2
Hãy chia các số cho trong bảng 2.1 thành hai nhóm: nhóm A gồm các số chỉ có hai ước, nhóm B gồm các số có nhiều hơn hai ước.
Gợi ý đáp án:
Từ bảng 2.1 hoàn thành trên, ta có bảng sau:
|
Nhóm A gồm các số chỉ có hai ước: |
2, 3, 5, 7, 11 |
|
Nhóm B gồm các số có nhiều hơn hai ước: |
4, 6, 8, 9, 10 |
Hoạt động 3
Suy nghĩ và trả lời câu hỏi:
a) Số 1 có bao nhiêu ước?
b) Số 0 có chia hết cho 2; 5; 7; 2 017; 2 018 không? Em có nhận xét gì về số ước của 0?
Gợi ý đáp án:
a) Số 1 có 1 ước đó chính là 1.
b) Số 0 chia hết cho 2; 5; 7; 2 017; 2 018 vì số 0 chia cho số nào khác 0 cũng bằng 0.
Do đó số 0 có vô số ước.
Giải Toán 6 Kết nối tri thức với cuộc sống Bài 10 – Luyện tập
Luyện tập 1
Em hãy tìm nhà thích hợp cho các ô trong bảng 2.1
| Số | Các ước | Số ước |
| 2 | 1, 2 | 2 |
| 3 | 1, 3 | 2 |
| 4 | 1, 2, 4 | 3 |
| 5 | 1, 5 | 2 |
| 6 | 1, 2, 3, 6 | 4 |
| 7 | 1, 7 | 2 |
| 8 | 1, 2, 4, 8 | 4 |
| 9 | 1, 3, 9 | 3 |
Gợi ý đáp án:
Số nguyên tố: 11, 13, 17, 19, 23, …
Hợp số: 10, 12, 14, 15, 16, 18, 20, 21, 22, …
Luyện tập 2
Trong các số cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao?
a) 1 930 b) 23
Gợi ý đáp án:
a) Số 1 930 có chữ số tận cùng là
=> 1 930 chia hết cho 2
Vậy 1 930 là hợp số
b) Số 23 là số nguyên tố vì nó lớn hơn 1 và chỉ có 2 ước là 1 và chính nó.
Luyện tập 3
Phân tích các số sau ra thừa số nguyên tố theo sơ đồ cột:
a) 36 b) 105
Gợi ý đáp án:
|
36 |
2 |
|
18 |
2 |
|
9 |
3 |
|
3 |
3 |
|
1 |
Kết quả: 36 = 22.32
|
105 |
3 |
|
35 |
5 |
|
7 |
7 |
|
1 |
Kết quả: 105 = 3.5.7
Giải Toán 6 Kết nối tri thức với cuộc sống phần Câu hỏi
Câu hỏi 1
Bạn Việt phân tích số 60 ra thừa số nguyên tố và cho kết quả 60 = 3 . 4. 5. Kết quả của Việt đúng hay sai? Nếu sai, em hãy sửa lại cho đúng.
Trả lời:
Vì 4 có 3 ước là: 1, 2, 4 nên 4 là hợp số.
Do đó trong phân tích 60 ra thừa số nguyên tố bạn Việt cho kết quả 60 = 3 . 4. 5 là sai.
Sửa lại kết quả đúng là:
60 = 2 . 2 . 3. 5 = 22.3.5
Câu hỏi 2
Tìm các số còn thiếu trong phân tích số 18 ra thừa số nguyên tố theo sơ đồ cây ở hình 2.3
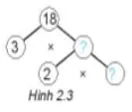
Trả lời:
+) Vì 18 = 3 x 6 nên ở ❔ đầu tiên từ trên xuống là 6
+) Vì 6 = 2 x 3 nên ở ❔ cuối cùng là 3
Vậy: 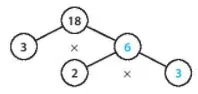
Câu hỏi 3
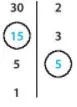
Tìm các số còn thiếu trong phân tích số 30 ra thừa số nguyên tố theo sơ đồ cột ở hình bên:
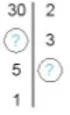
+) Vì 30 : 2 = 15 nên ở ❔ đầu tiên từ trên xuống là 15
+) Vì 5 : ❔ = 1
❔ = 5 : 1 = 5 nên ❔ cuối cùng là 5
Giải Toán 6 Kết nối tri thức với cuộc sống trang 41, 42 tập 1
Bài 2.17
Phân tích các số sau ra thừa số nguyên tố: 70; 115.
Gợi ý đáp án:
- 70 = 2 . 5. 7
- 115 = 5 . 23
Bài 2.18
Kết quả phân tích các số 120, 102 ra thừa số nguyên tố của Nam như sau:
120 = 2.3.4.5 ; 102 = 2.51
Theo em, kết quả của Nam đúng hay sai? Nếu sai, em hãy sửa lại cho đúng.
Gợi ý đáp án:
Kết quả của Nam là sai. Sửa lại:
- 120 = 23.3.5
- 102 = 2.3.17
Bài 2.19
Các khẳng định sau đúng hay sai? Vì sao?
- Ước nguyên tố của 30 là 5 và 6
- Tích của hai số nguyên bất kì luôn là số lẻ.
- Ước nguyên tố nhỏ nhất của số chẵn là 2
- Mọi bội của 3 đều là hợp số
- Mọi số chẵn đều là hợp số
Gợi ý đáp án:
- Sai. Vì số 6 là hợp số.
- Sai. Vì tích của một số nguyên tố bất kì với số 2 luôn là số chẵn.
- Đúng. Vì 2 là số nguyên tố nhỏ nhất và mọi số chẵn đều chia hết cho 2.
- Sai. Vì 3 là bội của 3 nhưng nó là số nguyên tố
- Sai. Vì 2 là số chẵn nhưng nó là số nguyên tố
Bài 2.20
Kiểm tra xem các số sau là hợp số hay số nguyên tố bằng cách dùng dấu hiệu của chia hết hoặc tra bảng số nguyên tố:
89 , 97 , 125 , 541 , 2 013 , 2 018
Gợi ý đáp án:
- Các số nguyên tố là: 89 ; 97 ; 541
- Các hợp số là: 125 ; 2 013; 2 018
Bài 2.21
Hãy phân tích A ra thừa số nguyên tố:
A = 44.95
Gợi ý đáp án:
A = 44.95
= 4.4.4.4.9.9.9.9.9
= 22.22.22.22.32.32.32.32.32
= 22+2+2+2.32+2+2+2+2
= 28.310
Bài 2.22
Tìm các số còn thiếu trong các sơ đồ phân tích một số ra thừa số nguyên tố sau:
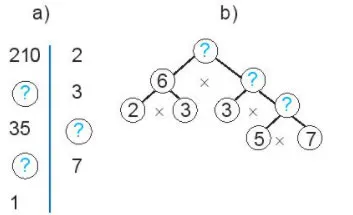
Gợi ý đáp án:
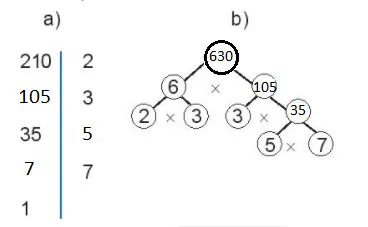
Bài 2.23
Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau và có nhiều hơn 1 người trong mỗi nhóm. Hỏi mỗi nhóm có thể có bao nhiêu người?
Gợi ý đáp án:
Phân tích 30 ra thừa số nguyên tố ta được: 30 = 2.3.5
Ta có bảng sau:
| Số nhóm | Số người một nhóm |
| 2 | 15 |
| 3 | 10 |
| 5 | 6 |
| 6 | 5 |
| 10 | 3 |
| 15 | 2 |
Bài 2.24
Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hàng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng, sao cho mỗi hàng có số người như nhau?

Các cách sắp xếp 33 chiến sĩ là:
- 11 hàng mỗi hàng 3 người
- 3 hàng mỗi hàng 11 người
Vậy có 2 cách sắp xếp.