Giải Toán lớp 6 Bài tập cuối chương 2 bao gồm đáp án chi tiết, cùng hướng dẫn giải các bài tập trong SGK Toán 6 Tập 1 Chân trời sáng tạo trang 73.
Bạn đang đọc: Toán 6 Bài tập cuối chương 2 – Chân trời sáng tạo
Lời giải Toán 6 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương 2: Số nguyên. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 6 Bài tập cuối chương 2 Chân trời sáng tạo
Giải Toán 6 Chân trời sáng tạo phần Trắc nghiệm trang 73 tập 1
Câu 1
Chọn phát biểu đúng trong số các câu sau:
(A) Tập hợp số nguyên được kí hiệu là N.
(B) +2 không phải là một số tự nhiên.
(C) 4 không phải là một số nguyên.
(D) – 5 là một số nguyên.
Lời giải chi tiết:
(A) Tập hợp số nguyên được kí hiệu là Z.
=> Đáp án A sai.
(B) + 2 là một số tự nhiên
=> Đáp án B sai.
(C) 4 là một số nguyên
=> Đáp án C sai.
(D) – 5 là một số nguyên âm nên – 5 là một số nguyên
=> Đáp án D đúng.
Chọn đáp án D
Câu 2
Trong các phát biểu sau đây, phát biểu nào sai?
(A) 3 > – 4.
(B) – 5 > – 9.
(C) – 1
(D) – 9 > -8.
Lời giải chi tiết:
Vì trên trục số điểm – 9 nằm bên trái -8
=> -9
Vậy đáp án D sai
Đáp án D
Câu 3
Kết quả của phép tính: 25 – (9 – 10) + (28 – 4) là:
(A) 50.
(B) 2.
(C) – 2.
(D) 48.
Lời giải chi tiết:
25 – (9 – 10) + (28 – 4)
= 25 – (- 1) + 24
= 25 + 1 + 24
= 26 + 24
= 50.
Đáp án A.
Câu 4
Kết quả của phép tính: (- 4) . (+21) . (- 25) . (- 2) là:
(A) 420.
(B) 4 200.
(C) – 4 200.
(D) – 420.
Lời giải chi tiết:
(- 4) . (+21) . (- 25) . (- 2)
= [(-4) . (-25)] . [(+21) . (-2)] —-> tính chất giao hoán và kết hợp
= 100 . (-42)
= – 4 200.
Đáp án C
Giải Toán 6 Chân trời sáng tạo phần Tự luận trang 73 tập 1
Bài 1
Tính:
a) 73 – (2 – 9);
b) (- 45) – (27 – 8).
Hướng dẫn giải
Quy tắc nhân hai số nguyên khác dấu
– Tích của hai số nguyên khác dấu luôn luôn là một số nguyên âm.
– Khi nhân hai số nguyên khác dấu, ta nhân số dương với số đối của số âm rồi thêm dấu trừ (-) trước kết quả nhận được.
Quy tắc nhân hai số nguyên cùng dấu
– Khi nhân hai số nguyên cùng dương, ta nhân chúng như nhân hai số tự nhiên.
– Khi nhân hai số nguyên cùng âm, ta nhân hai số đối của chúng.
Gợi ý đáp án:
a) 73 – (2 – 9)
= 73 – (-7)
= 73 + 7
= 80
b) (- 45) – (27 – 8)
= (-45) – 19
= (-45) + (-19)
= -64
Bài 2
Tìm hai số nguyên x, thỏa mãn:
a) x2 = 4;
b) x2 = 81.
Hướng dẫn giải
Cho a, b ∈ Z. Nếu a ⋮ b thì ta nói a là bội của b là b là ước của a.
Nếu c vừa là ước của a, vừa là ước của b thì c cũng được gọi là ước chung của a và b.
Gợi ý đáp án:
a) x2= 4
x2 = 22 hoặc x2 = (-2)2
x = 2 hoặc x = -2
Vậy x = 2 hoặc x = -2
b) x2 = 81
x2 = 92 hoặc x2 = (-9)2
x = 9 hoặc x = – 9
Vậy x = 9 hoặc x = – 9
Bài 3
Tính các thương sau:
a) 12 : 6;
c) (- 36) : 9;
b) 24 : (- 8);
d) (- 14) : (- 7).
Hướng dẫn giải
Cho a, b ∈ Z. Nếu a ⋮ b thì ta nói a là bội của b là b là ước của a.
Nếu c vừa là ước của a, vừa là ước của b thì c cũng được gọi là ước chung của a và b.
Gợi ý đáp án:
a) 12 : 6 = 2
c) (- 36) : 9 = -4
b) 24 : (- 8) = -3
d) (- 14) : (- 7) = 2
Bài 4
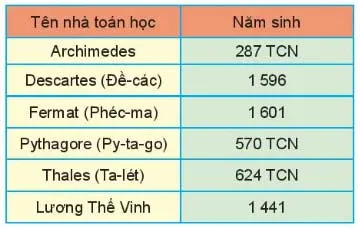
Cho biết năm sinh của một số nhà toán học.
Hướng dẫn giải
– Số nguyên âm được ghi như sau: -1; -2; -3; … và được đọc là âm một, âm hai, âm ba, … hoặc trừ một, trừ hai, trừ ba, …
– Mọi số nguyên dương đều lớn hơn số 0
– Mọi số nguyên âm đều nhỏ hơn số 0
– Mọi số nguyên âm đều nhỏ hơn bất kì số nguyên dương nào
– Với hai số nguyên âm, số nào có số đối lớn hơn thì số đó nhỏ hơn
Gợi ý đáp án:
Archimedes có năm sinh 287 TCN nghĩa là năm thứ -287;
Pythagore có năm sinh 570 TCN nghĩa là năm thứ – 570;
Thales có năm sinh 624 TCN nghĩa là năm thứ – 624;
Ta có: 1 601 > 1 596 > 1 441 > – 287 > – 570 > – 624.
Số chỉ các năm sinh giảm dần: 1 601; 1 596; 1 441; – 287; – 570; – 624.
Bài 5
Một máy bay đang bay ở độ cao 5 000 m trên mực nước biển, tình cờ thẳng ngay bên dưới máy bay có một chiếc tàu ngầm đang lặn ở độ sâu 1 200 m dưới mực nước biển. Tính khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm.

Hướng dẫn giải
– Phép cộng các số nguyên có các tính chất:
+ Tính chất giao hoán: a + b = b + a
+ Cộng với số 0: a + 0 = 0 + a = a
+ Tính chất kết hợp: (a + b) + c = a + (b + c)
– Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b
a – b = a + (-b)
Gợi ý đáp án:
Độ cao của tàu ngầm là: -1200 m.
Khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là:
5 000 – (-1 200) = 5 000 + 1 200 = 6 200 (m)
Vậy khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là 6 200 m.
Bài 6
Đố vui: Tìm số nguyên thích hợp thay thế cho mỗi dấu ? trong bảng dưới đây sao cho tích của ba số ở ba ô liền nhau đều bằng 0.
| ? | ? | 3 | ? | ? | ? | ? | ? | ? | -4 | ? |
Hướng dẫn giải:
Quy tắc nhân hai số nguyên khác dấu
– Tích của hai số nguyên khác dấu luôn luôn là một số nguyên âm.
– Khi nhân hai số nguyên khác dấu, ta nhân số dương với số đối của số âm rồi thêm dấu trừ (-) trước kết quả nhận được.
Quy tắc nhân hai số nguyên cùng dấu
– Khi nhân hai số nguyên cùng dương, ta nhân chúng như nhân hai số tự nhiên.
– Khi nhân hai số nguyên cùng âm, ta nhân hai số đối của chúng.
Gợi ý đáp án:
| 3 | a | b | c | d | -4 |
Theo quy luật, tích ở ba ô liên tiếp đều bằng 60, nghĩa là a.b.c = 60; b.c.d = 60
Suy ra: a.b.c = b.c.d => a = d
Do đó ta được dãy số:
| -4 | x | 3 | -4 | x | 3 | -4 | x | 3 | -4 | x |
Nhìn vào ta thấy: theo quy luật: x .. 3 . (-4) = 60 => x = -5
Vậy điền dãy số hoàn chỉnh như sau:
| -4 | -5 | 3 | -4 | -5 | 3 | -4 | -5 | 3 | -4 | -5 |
Bài 7
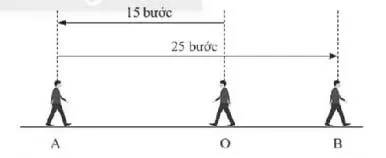
Hình vẽ dưới đây biểu diễn một người đi từ O đến A rồi quay về B. Đặt một bài toán phù hợp với hình vẽ.
Gợi ý đáp án:
Bài toán: Một người đang đứng yên ở điểm O, người đó bước đi về điểm A bên trái 15 bước, rồi đi ngược lại về điểm B bên phải 25 bước (biết rằng các bước chân của người đó là như nhau).
a) Hỏi người đó đi từ O đến B hết bao nhiêu bước
b) So sánh số trên với tổng của hai số nguyên (- 15) + 25.
Lời giải bài toán
a) Người đó đi từ O đến B hết số bước chân là: 25 -15 = 10 (bước).
b) Ta có: (-15) + 25 = 25 – 15 = 10.
Bài 8
Một công ty có 3 cửa hàng A, B, C. Kết quả kinh doanh sau một năm của từng cửa hàng như sau:
- Cửa hàng A: lãi 225 triệu đồng.
- Cửa hàng B: lỗ 280 triệu đồng.
- Cửa hàng C: lãi 655 triệu đồng.
Hỏi bình quân mỗi tháng công ty lãi hay lỗ bao nhiêu tiền từ ba cửa hàng đó?
Hướng dẫn giải:
Số nguyên âm được ghi như sau: -1; -2; -3; … và được đọc là âm một, âm hai, âm ba, … hoặc trừ một, trừ hai, trừ ba, …
Gợi ý đáp án:
Cửa hàng A lãi 225 triệu đồng được biểu diễn: 225 (triệu đồng).
Cửa hàng B lỗ 280 triệu đồng được biểu diễn: – 280 (triệu đồng).
Cửa hàng C lãi 665 triệu đồng được biểu diễn: 655 (triệu đồng).
Tổng kết quả kinh doanh trong 12 tháng của ba cửa hàng A, B, C là:
225 + (-280) + 655 = 600 (triệu đồng).
Mỗi tháng doanh thu của công ty là: 600:12 = 50 (triệu đồng).
Vậy bình quân mỗi tháng công ty lãi 50 triệu đồng từ ba cửa hàng A, B, C.
