Giải Toán lớp 7 bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 2 Kết nối tri thức với cuộc sống trang 72, 73, 74, 75, 76.
Bạn đang đọc: Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác
Lời giải Toán 7 Bài 34 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài 34 Chương IX – Quan hệ giữa các yếu tố trong một tam giác. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống tập 2 bài 34 – Luyện tập
Luyện tập 1
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.
Gợi ý đáp án:
Hình vẽ minh họa:
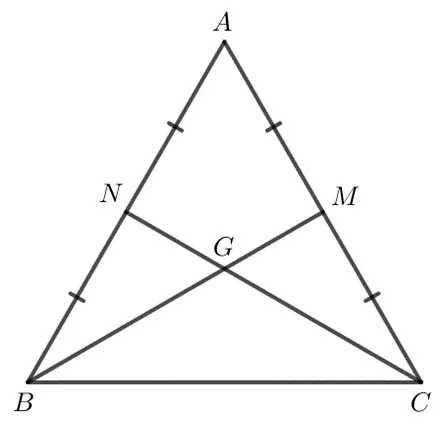
Gọi M là giao điểm của BG và AC, N là giao điểm của CG và AB.
Do ∆ABC đều nên AB = BC = CA và
M là trung điểm của AC => AM = MC
Xét tam giác ABM và tam giác CBM có:
AB = CB (chứng minh trên)
(chứng minh trên)
AM = CM (chứng minh trên)
=> ∆ABM = ∆CBM (c – g – c)
=> (Hai góc tương ứng)
Mà
=> BM ⊥ AC
BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của AC.
N là trung điểm của AB nên AN = BN.
Xét tam giác CAN và tam giác CBN có:
CA = CB (chứng minh trên)
(chứng minh trên)
AN = BN (chứng minh trên)
=> ∆CAN = ∆CBN (c – g – c)
=> (Hai góc tương ứng)
Mà
=> CN ⊥ AB
CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của AB.
G là giao điểm 2 đường trung trực của ∆ABC nên G cách đều 3 đỉnh của tam giác.
Luyện tập 2
a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Gợi ý đáp án:
a) Hình vẽ minh họa:
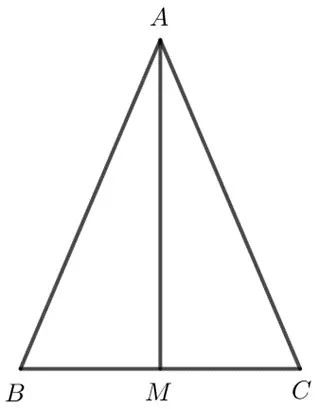
Gọi M là trung điểm của BC
Do tam giác ABC cân tại A nên AB = AC và
Do AB = AC nên A nằm trên đường trung trực của BC.
=> AM ⊥ BC nên AM là đường cao của tam giác ABC.
Xét tam giác ABM có:
(trong tam giác vuông, hai góc nhọn phụ nhau).
=>
Xét tam giác ACM có:
(trong tam giác vuông, hai góc nhọn phụ nhau).
=>
Mà
Từ (*) và (**) ta có:
=> AM là tia phân giác của
Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
b) Hình vẽ minh họa:
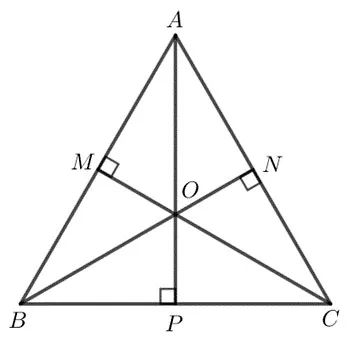
Trong tam giác ABC đều có điểm O là điểm cách đều 3 đỉnh của tam giác.
Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
Do O cách đều 3 đỉnh của tam giác ABC nên O là giao điểm 3 đường trung trực của tam giác ABC.
=> OM ⊥ AM, ON ⊥ AN, OP ⊥ CP.
Tam giác ABC đều => AB = AC = BC.
Do M, N, P lần lượt là trung điểm của AB, AC, BC nên AM = AN = NC = CP.
Xét tam giác OAM vuông tại M và tam giác OAN vuông tại N:
AM = AN (chứng minh trên)
OA chung
=> ∆OAM = ∆OAN (cạnh huyền – cạnh góc vuông)
=> OM = ON (2 cạnh tương ứng) (1)
Xét tam giác OCN vuông tại N và tam giác OCP vuông tại P:
CN = CP (chứng minh trên)
OC chung
=> ∆OCN = ∆OCP (cạnh huyền – cạnh góc vuông)
=> ON = OP (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra OM = ON = OP
Vậy trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Giải Toán 7 Kết nối tri thức với cuộc sống trang 76 tập 2
Bài 9.20
Cho tam giác ABC với hai đường trung tuyến BN,CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu ”?” để được các đẳng thức:
BG = ? BN, CG = ? CP; BG = ? GN, CG = ? GP
Gợi ý đáp án:
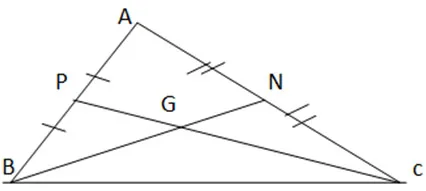
G là trọng tâm của tam giác ABC
 CG =frac{2}{3} CP => CG= 2 GP” width=”262″ height=”41″ data-type=”0″ data-latex=”=> CG =frac{2}{3} CP => CG= 2 GP” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20CG%20%3D%5Cfrac%7B2%7D%7B3%7D%20CP%20%3D%3E%20CG%3D%202%20GP”>
CG =frac{2}{3} CP => CG= 2 GP” width=”262″ height=”41″ data-type=”0″ data-latex=”=> CG =frac{2}{3} CP => CG= 2 GP” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20CG%20%3D%5Cfrac%7B2%7D%7B3%7D%20CP%20%3D%3E%20CG%3D%202%20GP”>
Tương tự:  BG= 2 GN” width=”233″ height=”41″ data-type=”0″ data-latex=”BG = frac{2}{3} BN => BG= 2 GN” data-src=”https://tex.vdoc.vn?tex=BG%20%3D%C2%A0%5Cfrac%7B2%7D%7B3%7D%20BN%20%3D%3E%20BG%3D%202%20GN”>
BG= 2 GN” width=”233″ height=”41″ data-type=”0″ data-latex=”BG = frac{2}{3} BN => BG= 2 GN” data-src=”https://tex.vdoc.vn?tex=BG%20%3D%C2%A0%5Cfrac%7B2%7D%7B3%7D%20BN%20%3D%3E%20BG%3D%202%20GN”>
Bài 9.21
Chứng minh rằng
a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau
b) Ngược lại nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân
Gợi ý đáp án:
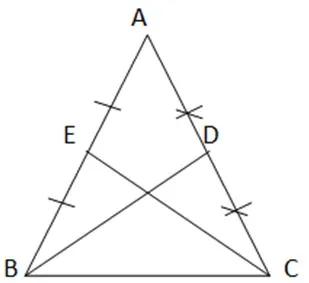
a) Ta có ∆ ABC cân tại A. BD và CE là trung tuyến với E là trung điểm của AB, D là trung điểm của AC
∆ ABC cân tại A => AB = AC
Có:
=> AE= AD
Xét ∆ ABD và ∆ ACE ta có:
chung
AE=AD
AB= AC
=> ∆ ABD = ∆ ACE => BD= CE
b)
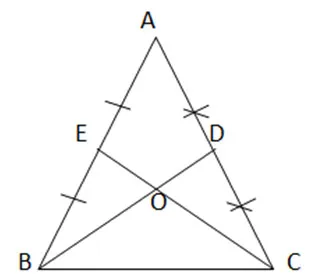
Gọi O là giao điểm của CE và BD
Ta có CE và BD là 2 đường trung tuyến nên O sẽ là trọng tâm của tam giác ∆ ABC
 BO = frac{2}{3} BD. OD= frac{1}{3} BD” width=”241″ height=”41″ data-type=”0″ data-latex=”=> BO = frac{2}{3} BD. OD= frac{1}{3} BD” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20BO%20%3D%C2%A0%5Cfrac%7B2%7D%7B3%7D%20BD.%20OD%3D%C2%A0%5Cfrac%7B1%7D%7B3%7D%20BD”>
BO = frac{2}{3} BD. OD= frac{1}{3} BD” width=”241″ height=”41″ data-type=”0″ data-latex=”=> BO = frac{2}{3} BD. OD= frac{1}{3} BD” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20BO%20%3D%C2%A0%5Cfrac%7B2%7D%7B3%7D%20BD.%20OD%3D%C2%A0%5Cfrac%7B1%7D%7B3%7D%20BD”>
CE= BD
=> BO= CO. OD= OE
Xét ∆ EOB và ∆ DOC ta có:
BO= OC
OD= OE
(2 góc đối đỉnh)
=> ∆ EOB = ∆ DOC
=> EB= DC
Có
=> AB= AC
=> ∆ ABC cân tại A
Bài 9.22
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Gợi ý đáp án:
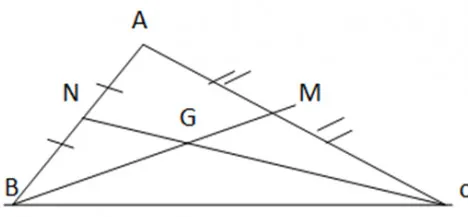
BM, CN là 2 đường trung tuyến cắt nhau tại
=> G là trọng tâm của tám giác ABC
 BG= frac{2}{3}BM, CG= frac{2}{3}CN” width=”246″ height=”41″ data-type=”0″ data-latex=”=> BG= frac{2}{3}BM, CG= frac{2}{3}CN” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20BG%3D%C2%A0%5Cfrac%7B2%7D%7B3%7DBM%2C%20CG%3D%20%5Cfrac%7B2%7D%7B3%7DCN”> (1)
BG= frac{2}{3}BM, CG= frac{2}{3}CN” width=”246″ height=”41″ data-type=”0″ data-latex=”=> BG= frac{2}{3}BM, CG= frac{2}{3}CN” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20BG%3D%C2%A0%5Cfrac%7B2%7D%7B3%7DBM%2C%20CG%3D%20%5Cfrac%7B2%7D%7B3%7DCN”> (1)
Xét theo định lí quan hệ giữa góc và cạnh tỏng tam giác ta có
Trong tam giác GBC:  widehat{GCB}” width=”111″ height=”23″ data-type=”0″ data-latex=”widehat{GBC} > widehat{GCB}” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BGBC%7D%20%3E%C2%A0%5Cwidehat%7BGCB%7D”>
widehat{GCB}” width=”111″ height=”23″ data-type=”0″ data-latex=”widehat{GBC} > widehat{GCB}” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BGBC%7D%20%3E%C2%A0%5Cwidehat%7BGCB%7D”>
=> CG > GB (2)
Từ (1) và (2) => CN > BM
Bài 9.23
Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC = 120°
Gợi ý đáp án:
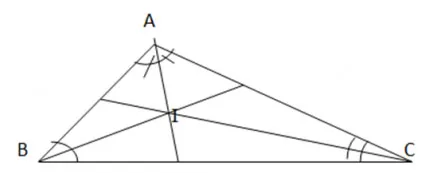
Có I là điểm đồng quy của ba đường phân giác trong tam giác ABC
=> AI, BI, CI lần lượt là đường phân giác của 3 góc
 widehat{ABC} +widehat{ACB} = 60°” width=”303″ height=”24″ data-type=”0″ data-latex=”widehat{BAC} = 120° => widehat{ABC} +widehat{ACB} = 60°” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BBAC%7D%20%3D%C2%A0120%C2%B0%20%3D%3E%C2%A0%5Cwidehat%7BABC%7D%20%2B%5Cwidehat%7BACB%7D%20%3D%2060%C2%B0″>
widehat{ABC} +widehat{ACB} = 60°” width=”303″ height=”24″ data-type=”0″ data-latex=”widehat{BAC} = 120° => widehat{ABC} +widehat{ACB} = 60°” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BBAC%7D%20%3D%C2%A0120%C2%B0%20%3D%3E%C2%A0%5Cwidehat%7BABC%7D%20%2B%5Cwidehat%7BACB%7D%20%3D%2060%C2%B0″>
Ta có:
 2 widehat{IBC} + 2 widehat{ICB} = 60°” width=”203″ height=”24″ data-type=”0″ data-latex=”=> 2 widehat{IBC} + 2 widehat{ICB} = 60°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%202%C2%A0%5Cwidehat%7BIBC%7D%20%2B%202%C2%A0%C2%A0%5Cwidehat%7BICB%7D%20%3D%C2%A060%C2%B0″>
2 widehat{IBC} + 2 widehat{ICB} = 60°” width=”203″ height=”24″ data-type=”0″ data-latex=”=> 2 widehat{IBC} + 2 widehat{ICB} = 60°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%202%C2%A0%5Cwidehat%7BIBC%7D%20%2B%202%C2%A0%C2%A0%5Cwidehat%7BICB%7D%20%3D%C2%A060%C2%B0″>
 widehat{IBC} + widehat{ICB} = 30°” width=”185″ height=”24″ data-type=”0″ data-latex=”=> widehat{IBC} + widehat{ICB} = 30°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BIBC%7D%20%2B%C2%A0%C2%A0%C2%A0%5Cwidehat%7BICB%7D%20%3D%2030%C2%B0″>
widehat{IBC} + widehat{ICB} = 30°” width=”185″ height=”24″ data-type=”0″ data-latex=”=> widehat{IBC} + widehat{ICB} = 30°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BIBC%7D%20%2B%C2%A0%C2%A0%C2%A0%5Cwidehat%7BICB%7D%20%3D%2030%C2%B0″>
Xét trong tam giác IBC ta có:
 widehat{BIC} = 180° – 30°= 150°” width=”246″ height=”24″ data-type=”0″ data-latex=”=> widehat{BIC} = 180° – 30°= 150°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BBIC%7D%20%3D%C2%A0180%C2%B0%20-%C2%A030%C2%B0%3D%20150%C2%B0″>
widehat{BIC} = 180° – 30°= 150°” width=”246″ height=”24″ data-type=”0″ data-latex=”=> widehat{BIC} = 180° – 30°= 150°” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BBIC%7D%20%3D%C2%A0180%C2%B0%20-%C2%A030%C2%B0%3D%20150%C2%B0″>
Bài 9.24
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chúng minh BE= CF
Gợi ý đáp án:
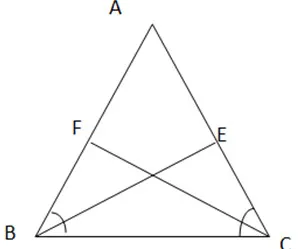
∆ABC cân tại A
 AB = AC. widehat{ABC} = widehat{ACB} (1)” width=”256″ height=”28″ data-type=”0″ data-latex=”=> AB = AC. widehat{ABC} = widehat{ACB} (1)” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20AB%20%3D%20AC.%C2%A0%5Cwidehat%7BABC%7D%20%3D%C2%A0%5Cwidehat%7BACB%7D%20(1)”>
AB = AC. widehat{ABC} = widehat{ACB} (1)” width=”256″ height=”28″ data-type=”0″ data-latex=”=> AB = AC. widehat{ABC} = widehat{ACB} (1)” data-src=”https://tex.vdoc.vn?tex=%3D%3E%20AB%20%3D%20AC.%C2%A0%5Cwidehat%7BABC%7D%20%3D%C2%A0%5Cwidehat%7BACB%7D%20(1)”>
BE là đường phân giác của  widehat{ABE} = frac{1}{2} widehat{ABC} (2)” width=”230″ height=”40″ data-type=”0″ data-latex=”widehat{ABC} => widehat{ABE} = frac{1}{2} widehat{ABC} (2)” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BABC%7D%20%3D%3E%C2%A0%5Cwidehat%7BABE%7D%20%3D%C2%A0%5Cfrac%7B1%7D%7B2%7D%C2%A0%5Cwidehat%7BABC%7D%20(2)”>
widehat{ABE} = frac{1}{2} widehat{ABC} (2)” width=”230″ height=”40″ data-type=”0″ data-latex=”widehat{ABC} => widehat{ABE} = frac{1}{2} widehat{ABC} (2)” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BABC%7D%20%3D%3E%C2%A0%5Cwidehat%7BABE%7D%20%3D%C2%A0%5Cfrac%7B1%7D%7B2%7D%C2%A0%5Cwidehat%7BABC%7D%20(2)”>
CF là đường phân giác của  widehat{ACF} = frac{1}{2} widehat{ACB} (3)” width=”230″ height=”40″ data-type=”0″ data-latex=”widehat{ACB} => widehat{ACF} = frac{1}{2} widehat{ACB} (3)” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BACB%7D%20%3D%3E%C2%A0%5Cwidehat%7BACF%7D%20%3D%C2%A0%5Cfrac%7B1%7D%7B2%7D%C2%A0%5Cwidehat%7BACB%7D%20(3)”>
widehat{ACF} = frac{1}{2} widehat{ACB} (3)” width=”230″ height=”40″ data-type=”0″ data-latex=”widehat{ACB} => widehat{ACF} = frac{1}{2} widehat{ACB} (3)” data-src=”https://tex.vdoc.vn?tex=%5Cwidehat%7BACB%7D%20%3D%3E%C2%A0%5Cwidehat%7BACF%7D%20%3D%C2%A0%5Cfrac%7B1%7D%7B2%7D%C2%A0%5Cwidehat%7BACB%7D%20(3)”>
Từ (1), (2), (3)  widehat{ABE} = widehat{ACF}” width=”143″ height=”23″ data-type=”0″ data-latex=”=> widehat{ABE} = widehat{ACF}” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BABE%7D%20%3D%C2%A0%5Cwidehat%7BACF%7D”>
widehat{ABE} = widehat{ACF}” width=”143″ height=”23″ data-type=”0″ data-latex=”=> widehat{ABE} = widehat{ACF}” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BABE%7D%20%3D%C2%A0%5Cwidehat%7BACF%7D”>
Xét ∆ ABE và ∆ ACF, ta có:
chung
AB= AC
=> ∆ ABE = ∆ ACF
=> BE = CF
Bài 9.25
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB
a) Hãy giải thích tại sao DP = DR
b) Hãy giải thích tại sao DP = DQ
c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A
Gợi ý đáp án:
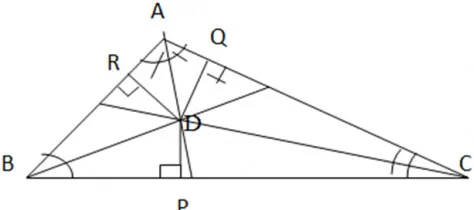
a) Ta có ∆ BPD và ∆ BRD đều là tam giác vuông tại và
Xét 2 tam giác vuông là ∆BRD và ∆BPD ta có:
Chung cạnh BD
(BD là phân giác của
hay
)
=> ∆BRD = ∆BPD
=> DR=DP
b) Ta có ∆ CPD và ∆ CQD đều là tam giác vuông tại và
Xét 2 tam giác vuông là ∆CPD và ∆CQD ta có:
Chung cạnh CD
(CD là phân giác của
hay
)
=> ∆ CPD = ∆CQD
=> DP = DQ
c) Từ a và b ta có DR = DQ
Xét 2 tam giác vuông là ∆ARD và ∆AQD ta có:
Chung cạnh AD
DR = DQ
=> ∆ ARD = ∆AQD
 widehat{RAD} = widehat{QAD}” width=”146″ height=”26″ data-type=”0″ data-latex=”=> widehat{RAD} = widehat{QAD}” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BRAD%7D%20%3D%C2%A0%5Cwidehat%7BQAD%7D”>
widehat{RAD} = widehat{QAD}” width=”146″ height=”26″ data-type=”0″ data-latex=”=> widehat{RAD} = widehat{QAD}” data-src=”https://tex.vdoc.vn?tex=%3D%3E%C2%A0%5Cwidehat%7BRAD%7D%20%3D%C2%A0%5Cwidehat%7BQAD%7D”>
=> D nằm trên đường phân giác của

