Giải bài tập SGK Toán 7 Tập 2 trang 67, 68, 69, 70 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 5: Đường trung trực của một đoạn thẳng.
Bạn đang đọc: Toán 7 Bài 5: Đường trung trực của một đoạn thẳng
Thông qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 5 Chương 8 – Tam giác trong sách giáo khoa Toán 7 Tập 2 Chân trời sáng tạo. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 bài 5: Đường trung trực của một đoạn thẳng Chân trời sáng tạo
Giải Toán 7 Chân trời sáng tạo trang 70 tập 2
Bài 1
Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B
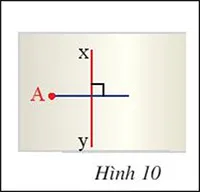
Gợi ý đáp án:
Gọi O là giao điểm của đường trung trực xy với đoạn thẳng AB
=> O là trung điểm của AB
Lấy điểm B thuộc đường thẳng OA sao cho O là trung điểm AB.
Bài 2
Quan sát hình 11, cho biết M là trung điểm BC, AM vuông góc với BC và AB = 10 cm. Tính AC.
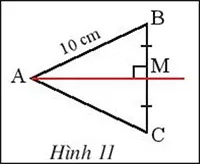
Gợi ý đáp án:
M là trung điểm của BC
AM ⊥ BC
=> AM là đường trung trực của BC
=> AB = AC
=> AC =10 cm.
Bài 3
Quan sát hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng 3 điểm A, M, D thẳng hàng.
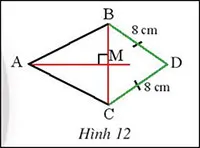
Gợi ý đáp án:
AM là đường trung trực của đoạn thẳng BC
=> AB = AC, MB = MC
Ta có DB = DC = 8 cm
=> D cách đều 2 đầu mút của đoạn thẳng AB
=> D thuộc đường trung trực của AB
=> A, M, D cùng thuộc đường trung trực của AB
=> A, M, D thẳng hàng.
Bài 4
Quan sát hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC
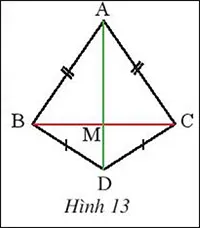
Gợi ý đáp án:
AB = AC => A thuộc đường trung trực của BC
DB= DC => D thuộc đường trung trực của BC
=> AD là đường trung trực của BC
Mà AD cắt BC tại M
=> M cũng thuộc đường trung trực AD
=> MB = MC
mà M thuộc BC
=> M là trung điểm của BC.
Bài 5
Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF
Chứng minh rằng ∆EMN = ∆FMN.
Gợi ý đáp án:
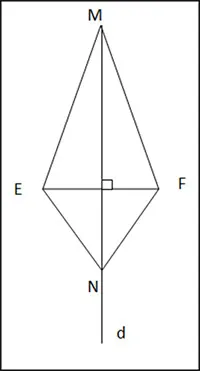
M, N thuộc đường trung trực d của đoạn thẳng EF
=> ME = MF, NE= NF
Xét ∆EMN và ∆FMN ta có:
ME = MF
NE = NF
MN chung
=> ∆EMN = ∆FMN (c.c.c)
Bài 6
Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình 14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.
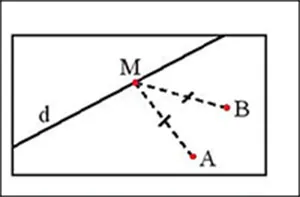
Gợi ý đáp án:
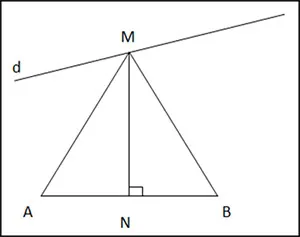
Gọi N là trung điểm của AB.
Qua N kẻ đường trung trực của đoạn thẳng AB, cắt đường thẳng d tại 1 điểm M.
=> M thuộc đường trung trực của AB
=> MA = MB
Vậy vị trí điểm M là nằm trên đường trung trực của đoạn thẳng AB.

