Giải Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→6 trang 88, 89, 90, 91, 92 tập 2.
Bạn đang đọc: Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Giải bài tập Toán 7 Cánh diều tập 2 trang 88, 89, 90, 91, 92 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán 7 Bài 6 trang 88, 89, 90, 91, 92 Cánh diều, mời các bạn cùng theo dõi.
Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Giải Toán 7 trang 91, 92 Cánh diều – Tập 2
Bài 1
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Gợi ý đáp án
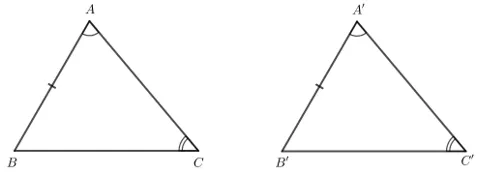
Xét tam giác ABC:
Xét tam giác A’B’C’:
Mà nên
Xét ∆ABC và ∆A’B’C’ có:
(theo giả thiết).
AB = A’B’ (theo giả thiết).
(theo giả thiết).
Do đó ∆ABC = ∆A’B’C’ (g – c – g).
Bài 2
Cho Hình 65 có AM = BN,
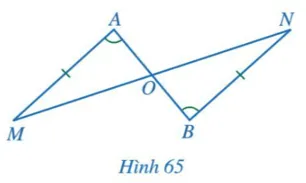
Chứng minh: OA = OB, OM = ON.
Gợi ý đáp án
Xét ∆AOM có:
Xét ∆BON có:
Mà (theo giả thiết),
(2 góc đối đỉnh).
Do đó
Xét ∆AOM và ∆BON có:
(theo giả thiết)
AM = BN (theo giả thiết).
(chứng minh trên).
Suy ra ∆AOM = ∆BON (g – c – g).
Do đó OA = OB (2 cạnh tương ứng), OM = ON (2 cạnh tương ứng).
Bài 3
Cho Hình 66 có . Chứng minh MN = QP, MP = QN.
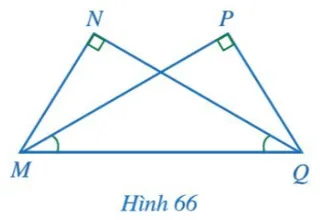
Gợi ý đáp án
Tam giác MNQ có nên tam giác MNQ vuông tại N.
Tam giác QPM có nên tam giác QPM vuông tại P.
Xét ∆MNQ vuông tại N và ∆QPM vuông tại P có:
(theo giả thiết).
MQ chung.
Suy ra ∆MNQ = ∆QPM (cạnh huyền – góc nhọn).
Do đó MN = QP (2 cạnh tương ứng), MP = QN (2 cạnh tương ứng).
Bài 4
Cho Hình 67 có , DH = CK,
.
Chứng minh AD = BC.
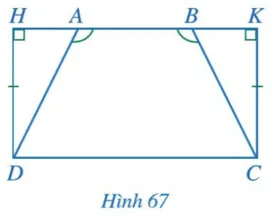
Gợi ý đáp án
Ta thấy là góc ngoài tại đỉnh A của tam giác AHD nên
hay
là góc ngoài tại đỉnh B của tam giác BKC nên
hay
Mà nên
Xét ∆AHD vuông tại H và ∆BKC vuông tại K có: (chứng minh trên).
DH = CK (theo giả thiết).
Suy ra ∆AHD = ∆BKC (góc nhọn – cạnh góc vuông).
Do đó AD = BC (2 cạnh tương ứng).
Bài 5
Cho tam giác ABC có 
hat{C}” width=”53″ height=”21″ data-type=”0″ data-latex=”hat{B} > hat{C}” data-src=”https://tex.vdoc.vn/?tex=%5Chat%7BB%7D%20%3E%20%5Chat%7BC%7D”>. Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh
b) Kẻ tia Dx nằm trong góc ADC sao cho . Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: ∆ABD = ∆AED, AB
Gợi ý đáp án
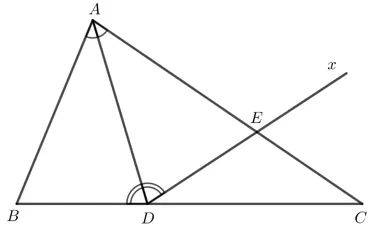
a) là góc ngoài tại đỉnh D của tam giác ADC nên
là góc ngoài tại đỉnh D của tam giác ADB nên
Do AD là tia phân giác của nên
Mà hat{ACD}” width=”112″ height=”21″ data-type=”0″ data-latex=”hat{ABD} > hat{ACD}” data-src=”https://tex.vdoc.vn/?tex=%5Chat%7BABD%7D%20%3E%20%5Chat%7BACD%7D”> nên
→
b) Xét ∆ABD và ∆AED có:
(chứng minh trên).
AD chung.
(theo giả thiết).
Suy ra ∆ABD = ∆AED (g – c – g).
Do đó AB = AE.
Mà AE
Vậy ∆ABD = ∆AED và AB
Bài 6
Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và N MP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.
Gợi ý đáp án
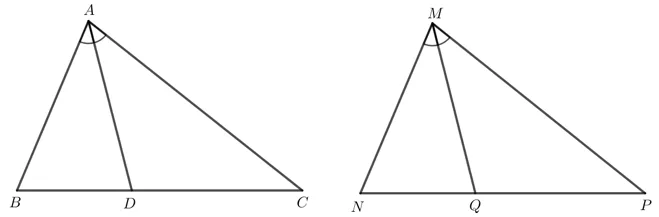
Do ∆ABC = ∆MNP nên (2 góc tương ứng),
(2 góc tương ứng) và AC = MP (2 cạnh tương ứng).
Do AD là tia phân giác của nên
Do MQ là tia phân giác của nên
Mà nên
Xét ∆ADC và ∆MQP có:
(chứng minh trên).
AC = MP (chứng minh trên).
(chứng minh trên).
Suy ra ∆ADC = ∆MQP (g – c – g).
Do đó AD = MQ (2 cạnh tương ứng).
