Giải Toán lớp 7 Luyện tập chung trang 37, 38 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống.
Bạn đang đọc: Toán 7 Luyện tập chung trang 37
Lời giải Toán 7 Luyện tập trung trang 37 trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung Chương II: Số thực. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Giải Toán 7 bài Luyện tập chung trang 37 Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống trang 38 tập 1
Bài 2.19
Cho các phân số:
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết , hãy so sánh phân số tìm được trong câu a) với
Hướng dẫn giải:
– Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.
– Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.
Gợi ý đáp án:
a) Ta có:
=> Số không viết được dưới dạng số thập phân hữu hạn là:
b) Ta có: mà
1,414213562=>frac{133}{91}>sqrt{2}” width=”337″ height=”41″ data-type=”0″ data-latex=”1,(461538)>1,414213562=>frac{133}{91}>sqrt{2}” data-src=”https://tex.vdoc.vn?tex=1%2C(461538)%3E1%2C414213562%3D%3E%5Cfrac%7B133%7D%7B91%7D%3E%5Csqrt%7B2%7D”>
Bài 2.20
a. Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để chỉ rõ chu kì):. Em có nhận xét gì về kết quả nhận được?
b. Em hãy dự đoán dạng thập phân của ?
Hướng dẫn giải:
– Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.
– Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.
Gợi ý đáp án:
a. Viết dạng thập phân vô hạn tuần hoàn:
Nhận xét: Với phân số có dạng thì dạng thập phân vô hạn tuần hoàn của nó sẽ là 0,(00..1) với n số 9 thì có n-1 số 0
b. Dự đoán dạng thập phân của
Bài 2.21
Viết số và
dưới dạng số thập phân vô hạn tuần hoàn.
Hướng dẫn giải:
– Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.
– Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.
Gợi ý đáp án:
Bài 2.22
Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B,C như sau:
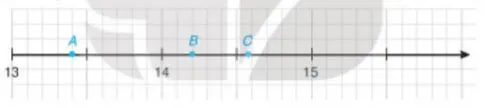
a. Hãy cho biết hai điểm A,B biểu diễn những số thập phân nào?
b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Hướng dẫn giải:
– Các số thập phân chỉ gồm hữu hạn số sau dấu “,” được gọi là số thập phân hữu hạn.
– Các số thập phân vô hạn tuần hoàn có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi.
Gợi ý đáp án:
a. Điểm A, B biểu diễn những số thập phân sau:
- Điểm A biểu diễn số 13,4
- Điểm B biểu diễn số 14,2
b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05, ta được 14,6.
Bài 2.23
Thay dấu “?” bằng chữ số thích hợp.
a) -7,02
b) -15,3 ? 021
Gợi ý đáp án:
a) -7,02
b) -15,39021
Bài 2.24
So sánh:
a. 12,26 và 12,(24);
b. 31,3(5) và 29,9(8)
Gợi ý đáp án:
a. Ta có: 12,(24) = 12,2424… Vì so sánh số ở hàng phần chục ta có 4
b. Vì so sánh ở hàng chục ta có 3 > 2 nên 31,3(5) > 29,9(8)
Bài 2.25
Tính:
a.
b.
c.
Gợi ý đáp án:
a.
b.
c.
Bài 2.26
Tính:
a.
b.
Gợi ý đáp án:
a.
b.
