Toán 8 Bài 16: Đường trung bình của tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 1 trang 81, 82, 83.
Bạn đang đọc: Toán 8 Bài 16: Đường trung bình của tam giác
Giải Toán 8 Kết nối tri thức tập 1 trang 81 → 83 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 16 Chương IV: Định lí Thalès. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:
Toán 8 Bài 16: Đường trung bình của tam giác Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 trang 83
Bài 4.6
Tính các độ dài x, y trong Hình 4.18.
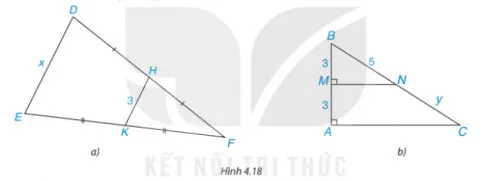
Bài giải:
a) HK là đường trung bình suy ra
b) Ta có:
Mặt khác M là trung điểm AB nên MN là đường trung bình của tam giác ABC
Suy ra N là trung điểm BC ⇒ y = BN = 5
Bài 4.7
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang
b) Tứ giác MNPB là hình gì? Tại sao?
Bài giải:
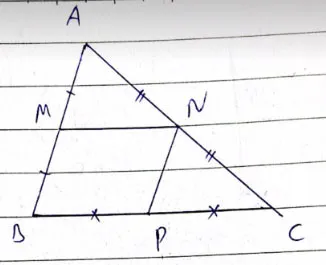
a) Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
suy ra MN // BC
Do đó tứ giác BMNC là hình thang
b) Ta có: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và
mà
nên MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành
Bài 4.8
Cho tam giác ABC có trung tuyến AM. Lấy hai điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E
a) Chứng minh DC // EM
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM
Bài giải:
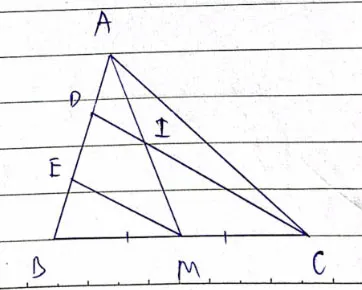
a) Xét ΔBDC có
E là trung điểm của BD(BE=ED; B,E,D thẳng hàng)
M là trung điểm của BC(gt)
Do đó: EM là đường trung bình của ΔBDC (Định nghĩa đường trung bình của tam giác)
⇒ ME//CD (Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE(AD=DE; A,D,E thẳng hàng)
DI//EM (cmt)
Do đó: I là trung điểm của AM (Định lí 1 về đường trung bình của tam giác)
nên AI=IM (đpcm)
Bài 4.9
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật
Bài giải:
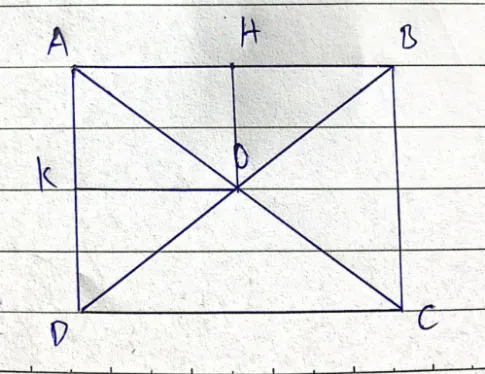
Ta có: OA = OB suy ra tam giác OAB cân tại B, OH là đường trung tuyến nên OH cũng là đường cao, do đó
Tương tự,
Xét tứ giác AHOK có: suy ra AHOK là hình chữ nhật

