Toán lớp 8 tập 1 trang 68, 69, 70, 71, 72 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 8 tham khảo.
Bạn đang đọc: Toán 8 Bài 3: Hình thang – Hình thang cân
Giải Toán 8 Chân trời sáng tạo Bài 3 Định lí Pythagore được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 71, 72. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán lớp 8 tập 1 chương III Bài 3 Hình thang – Hình thang cân Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.
Giải Toán 8 Bài 3: Hình thang – Hình thang cân
Toán 8 Tập 1 trang 81, 82 Chân trời sáng tạo
Bài tập 1
Tìm x và y ở các hình sau.
Gợi ý đáp án
MN // PQ suy ra
c) Ta có:
hay
d) Ta có: hay
Bài tập 2
Cho tứ giác ABCD có AB = CD, BD là tia phân giác góc B. Chứng minh rằng ABCD là hình thang
Gợi ý đáp án
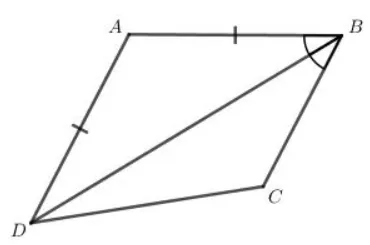
Xét tam giác ABD có AB=AD(gt)
⇒ΔABD cân tại A ⇒
Mà (BD là tia phân giác của góc B)
Do đó
Mà so le trong ⇒AD//BC
Vậy ABCD là hình thang.
Bài tập 3
Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN.
Gợi ý đáp án
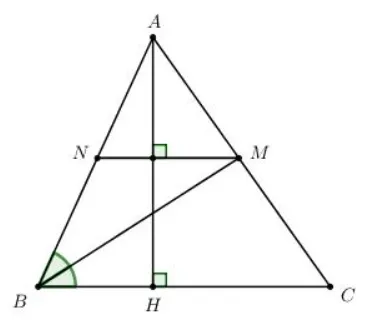
a) Ta có: MN⊥AH(gt)
Và BC⊥AH (AH là đường cao của tam giác ABC) ⇒MN//BC
Suy ra BCMN là hình thang
b) (BM là tia phân giác góc B)
Suy ra ⇒ ΔBMN cân tại N.
Vậy BN=MN
Bài tập 4
Cho tam giác ABC vuông tại A (AB
a) Chứng minh rằng: Δ A B D = Δ E B D
b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.
c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông.
Gợi ý đáp án
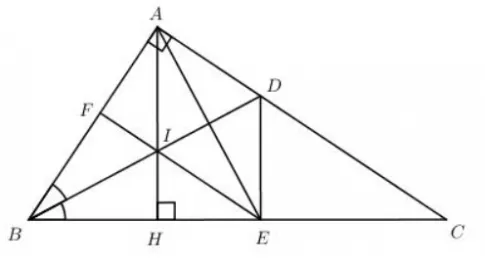
a) Xét ΔABD và ΔEBD ta có:
AB = BE (gt)
BD là cạnh chung
(BD là tia phân giác của góc B)
Do đó ΔABD = ΔEBD(c.g.c)
b) Ta có: (ΔEBD=ΔABD)
Mà
(ΔABD vuông tại A)
Nên ⇒DE⊥BC
Mặt khác AH⊥BC (gt) do đó DE // AH
⇒ Tứ giác ADEH là hình thang
Lại có (AH⊥BC)
Vậy tứ giác ADEH là hình thang vuông.
c) Ta có BE=BA(gt)⇒ cân tại B.
Mà BD là tia phân giác của góc B. Do đó BD là đường cao của tam giác BAE.
ΔBAEcó AH, BD là hai đường cao cắt nhau tại I ⇒I là trực tâm của tam giác BAE.
⇒ EFlà đường cao của tam giác BAE
⇒ EF⊥AB
Mà AC⊥AB⇒EF//AC
Vậy tứ giác ACEF là hình thang.
Mà . Do đó tứ giác ACEF là hình thang vuông.
Bài tập 5
Tứ giác nào trong Hình 15 là hình thang cân?
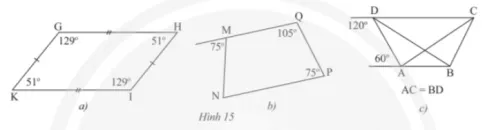
Gợi ý đáp án
a) Ta có: . Mà
là hai góc trong cùng phía suy ra GH // KI ⇒ GHKI là hình thang
Suy ra GHIK không là hình thang cân
b) Ta có: (hai góc kề bù)
Do đó
Ta có: . Mà
là hai góc trong cùng phía suy ra MQ // PN ⇒MQPN là hình thang
Lại có: Do đó MQPN là hình thang cân
c) Ta có: . Mà
và
là hai góc trong cùng phía suy ra AB // CD⇒ABCD là hình thang
Lại có AC = BD suy ra ABCD là hình thang cân
Bài tập 6
Cho hình thang ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác góc CEB.
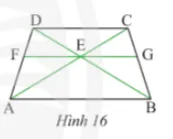
Gợi ý đáp án
Xét tam giác ACD và BDC ta có:
AD = BC (gt)
AC = BD (gt)
CD chung
Suy ra (c.c.c)
Ta có: FG // CD suy ra (đồng vị),
(so le trong)
Suy ra hay EG là tia phân giác góc CEB.
