Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 79, 80, 81, 82.
Bạn đang đọc: Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Giải bài tập Toán 8 Cánh diều tập 2 trang 79 → 82 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 7 Chương VIII: Tam giác đồng dạng, hình đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:
Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác Cánh diều
Giải Toán 8 Cánh diều Tập 2 trang 81, 82
Bài 1
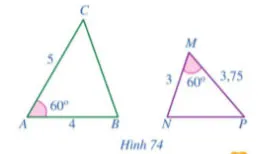
Cho Hình 74.
a) Chứng minh ABC
MNP.
b) Góc nào của tam giác MNP bằng góc B?
c) Góc nào của tam giác ABC bằng góc P?
Lời giải:
a) Ta có: ;
Suy ra: mà
Do đó: ABC
MNP.
b) Góc N của tam giác MNP bằng góc B.
c) Góc C của tam giác ABC bằng góc P.
Bài 2
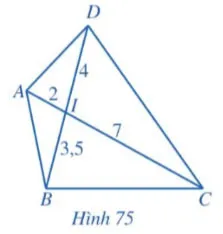
Cho Hình 75, chứng minh:
a) IAB
IDC;
b) IAD
IBC.
Lời giải:
a) Ta có: ;
Suy ra:
Mà (hai góc đối đỉnh)
Do đó: IAB
IDC (c.g.c).
b) Ta có: ;
Suy ra:
Mà (hai góc đối đỉnh)
Do đó: IAD
IBC (c.g.c)
Bài 3
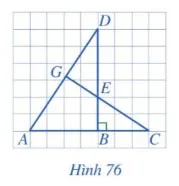
Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) ABD
EBC;
b) ;
c) Tam giác DGE vuông.
Lời giải:
a) Ta có: ;
Suy ra:
Mà
Do đó: ABD
EBC (c.g.c).
b) Vì ABD
EBC (cmt) nên
Mà (hai góc đối đỉnh)
Suy ra: .
c) Tam giác DAB vuông tại B có:
Mà (cmt)
Suy ra: hay
Do đó: Tam giác DGE vuông tại G.
Bài 4
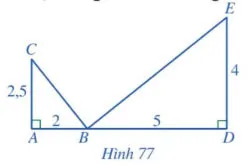
Cho Hình 77, chứng minh:
a) ;
b) BC BE.
Lời giải:
a) Ta có: ;
Suy ra:
Mà
Do đó: ABC
DEB (c.g.c)
Nên .
b) Tam giác BED vuông tại D có:
Mà (cmt)
Suy ra:
Mà
Do đó:
Hay BC BE.
Bài 5
Cho ABC
MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ABD
MNQ.
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh ABG
MNK.
Lời giải:
a) Ta có: ABC
MNP
Suy ra: và
Mà BC = 2BD (D là trung điểm BC); NP = 2NQ (Q là trung điểm NP)
Do đó: và
Suy ra: ABD
MNQ (c.g.c).
b) Ta có: ABD
MNQ (cmt)
Suy ra: và
Mà AD = AG (G là trọng tâm tam giác ABC); MQ =
MK (K là trọng tâm tam giác MNP)
Do đó: và
Suy ra: ABG
MNK (c.g.c).
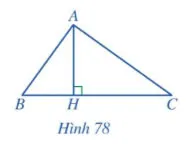
Bài 6
Cho Hình 78, biết = BH.CH. Chứng minh:
a) HAB
HCA;
b) Tam giác ABC vuông tại A.
Lời giải:
a) Ta có: = BH.CH hay
Mà
Do đó: HAB
HCA (c.g.c)
b) Do HAB
HCA nên
(1)
Tam giác HAC vuông tại H có: (2)
Từ (1)(2) suy ra:
Do đó:
Nên tam giác ABC vuông tại A.
Bài 7
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thỏa mãn AB = 20 m, AC = 50 m, .
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, . Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’
6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Lời giải:
Đổi 20 m = 2000 cm; 50 m = 5000 cm
Ta có: ;
Suy ra:
Mà
Do đó: ABC
A’B’C’ (c.g.c)
Suy ra: mà B’C’
6,6 cm
Do đó: BC 6600 cm hay 66 m.

