Giải Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 83, 84, 85.
Bạn đang đọc: Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Giải bài tập Toán 8 Cánh diều tập 2 trang 83 → 85 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 8 Chương VIII: Tam giác đồng dạng, hình đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:
Toán 8 Bài 8: Trường hợp đồng dạng thứ ba của tam giác Cánh diều
Giải Toán 8 Cánh diều Tập 2 trang 85
Bài 1
Cho Hình 86.
a) Chứng minh MNP
ABC.
b) Tìm x.
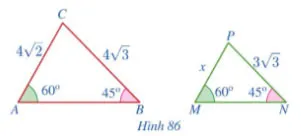
Lời giải:
a) Ta có: ;
Suy ra: MNP
ABC (g.g)
b) MNP
ABC nên
hay
Do đó: x = .
Bài 2
Cho hai tam giác ABC và PMN thỏa mãn ,
,
,
. Chứng minh
.
Lời giải:
Tam giác MNP có:
Mà ,
Suy ra: .
Ta có: ;
Suy ra: ABC
PMN (g.g)
Do đó: .
Bài 3
Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:
a) ACD
BCE và CA . CE = CB . CD;
b) ACD
AHE và AC . AE = AD . AH.
Lời giải:
a) Ta có: ; chung góc C
Suy ra: ACD
BCE (g.g)
Do đó: hay CA . CE = CB . CD.
b) Ta có: ; chung góc A
Suy ra: ACD
AHE (g.g)
Do đó: hay AC . AE = AD . AH.
Bài 4
Cho Hình 87 với . Chứng minh:
a) OAD
OCB;
b) ;
c) OAC
ODB.
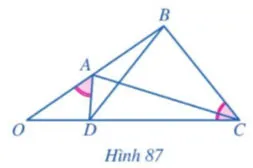
Lời giải:
a) Ta có: ; chung góc O
Suy ra: OAD
OCB (g.g)
b) Do OAD
OCB nên
Hay .
c) Ta có: (cmt) và chung góc O
Suy ra: OAC
ODB (c.g.c)
Bài 5
Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:
a) ABC
HBA và
= BC . BH;
b) ABC
HAC và
= BC . CH;
c) ABH
CAH và
= BH . CH;
d) .
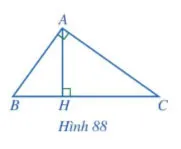
Lời giải:
a) Ta có: ; chung góc B
Suy ra: ABC
HBA (g.g)
Do đó:
Hay = BC . BH.
b) Ta có: ; chung góc C
Suy ra: ABC
HAC (g.g)
Do đó:
Hay = BC . CH.
c) Ta có: ABC
HBA
Mà ABC
HAC
Suy ra: ABH
CAH
Do đó:
Hay = BH . CH.
d) Ta có: = BC . BH. Suy ra:
= BC . CH. Suy ra:
= BH . CH. Suy ra:
(1)
Ta có: (2)
Từ (1)(2) suy ra: .
Bài 6
Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là AH = 2,8 m và AK = 1,6 m. Em hãy tính chiều cao của cây.
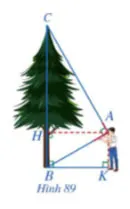
Lời giải:
Chiều cao của cây là đoạn thẳng BC.
Ta có: AHBK là hình chữ nhật nên AK = BH = 1,6 m
Tam giác AHB vuông tại H: AB =
Ta có: ; chung góc B
Suy ra: HBA
ABC
Do đó:
Suy ra: BC = = 6,5 m.

