Download.vn Học tập Lớp 10
Bạn đang đọc: Tổng hợp các bài tập về đường tròn lớp 10
Tổng hợp các bài tập về đường tròn lớp 10 Tài liệu ôn tập lớp 10 môn Toán
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Nhằm cung cấp thêm nền tảng về kiến thức chuyên đề Oxy cũng như củng cố thêm kỹ năng giải bài toán về đường tròn Download.vn xin giới thiệu tài liệu Tổng hợp các bài tập về đường tròn lớp 10.
Các bài toán liên quan đến đường tròn là những bài toán rất thú vị, vừa khó vừa hay và được sử dụng nhiều trong các bài toán Oxy. Hy vọng đây là tài liệu bổ ích giúp các bạn học sinh lớp 10 có thêm nhiều tài liệu tham khảo ôn tập môn Hình học đạt được kết quả cao. Sau đây là nội dung chi tiết, mời các bạn cùng theo dõi.
Tổng hợp các bài tập về đường tròn lớp 10
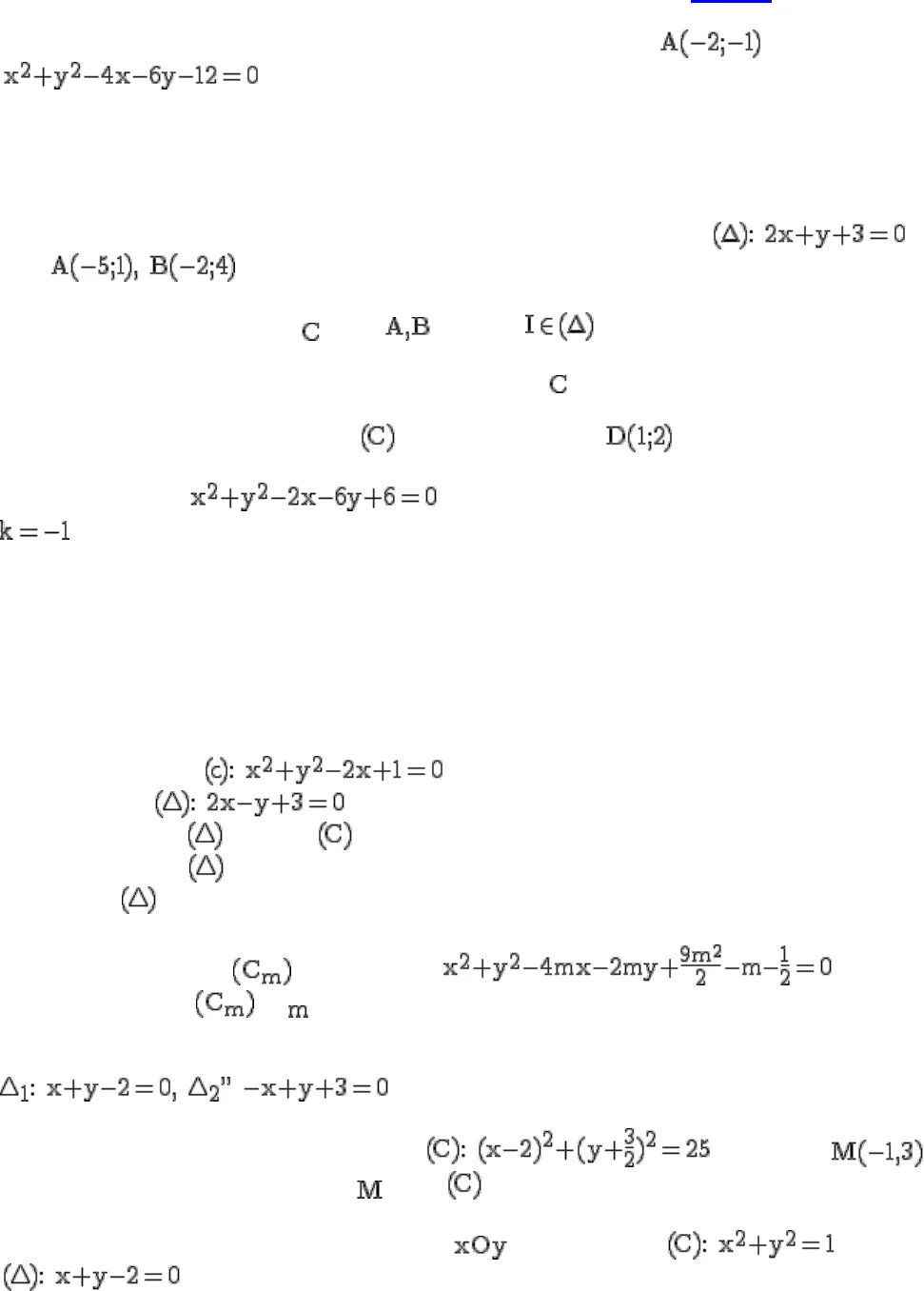Tổng hợp các bài tập về đường tròn lớp 10BT1: .Trong mặt phẳng với hệ tọa độ Đềcác vuông góc Oxy , cho điểm và đường tròn (O) :1. Chứng minh rằng A là một điểm nằm ngoài đường tròn (O).2. Viết phương trình các đường thẳng đi qua điểm A và tiếp xúc với đường tròn (O).BT2: Trong mặt phẳng với hệ tọa độ Đềcác vuông góc Oxy cho đường thẳng và haiđiểm1. Viết phương trình đường tròn đi qua và có tâm .2. Viết phương trình đường tiếp tuyến tại A với đường tròn .3. Viết phương trình các tiếp tuyến với , biết tiếp tuyến đi qua . Tìm tọa độ tiếp điểm .BT3: Cho đường tròn . Viết phương trình các tiếp tuyến của đường tròn có hệ số góc.BT4 : Trong mặt phẳng với hệ tọa độ Oxy cho điểm I(- 2; 1) và đường thẳng d : 3x – 4y = 0a. Viết phương trình đường tròn (C) có tâm I và tiếp xúc với đường thẳng d.b. Viết phương trình tập hợp các điểm mà qua các điểm đó vẽ được hai tiếp tuyến đến (C) sao cho hai tiếptuyến vuông góc với nhau.BT5: Cho đường trònVà đường thẳnga. Chứng minh rằng không cắtb. Từ điểm M thuộc kẻ các tiếp tuyến MA, MB tới (C) (A, B là các tiếp điểm). Chứng minh rằng khi Mthay đổi trên thì AB luôn đi qua một điểm cố định.BT6: Cho họ đường tròn có phương trình:Tìm tập hợp tâm của khi thay đổi.BT7: Viết phương trình đường tròn đi qua A(1,0) và tiếp xúc với hai đường thẳngBT8: Trong mặt phẳng tọa độ cho đường tròn và một điểm .Viết phương trình đường thẳng đi qua và cắt theo một dây cung có độ dài 8BT9: Trong mặt phẳng với hệ Đề các trực chuẩn , cho đường tròn và đường thẳng
a. Chứng minh rằng từ một điểm M bất kỳ trên ta luôn kẻ được hai tiếp tuyến phân biệt tới (C).b. Giả sử hai tiếp tuyến từ M tới (C) có các tiếp điểm là A và B. Chứng minh rằng khi M chạy trênđường thẳng AB luôn đi qua một điểm cố định.BT10: Cho đường tròn và đường thẳng ( là thamsố).a. Chứng minh rằng luôn cắt tại hai điểm phân biệt .b. Tìm để độ dài đoạn luôn đạt giá trị lớn nhất, nhỏ nhấtBT11: Cho họ đường tròn có phương trình:Chứng minh rằng luôn tiếp xúc với hai đường thẳng cố địnhBT12: Trong mặt phẳng tọa độ cho có phương trình .Viết phương trìnhcác tiếp tuyến kẻ từ điểm đến .BT13: Cho hai đường tròncó tâm lần lượt là và1. Chứng minh tiếp xúc ngoài với và tìm tọa độ tiếp điểm .2. Gọi là một tiếp tuyến chung không đi qua của và . Tìm tọa độ giao điểm của vàđường thẳng .Viết phương trình đường trong đi qua và tiếp xúc với hai đường tròn và tại .BT14: Trong mặt phẳng với hệ tạo độ vuông góc Oxy, xét họ đường tròn có phương trình( là tham số).Xác định tọa độ của tâm đường tròn thuộc họ đã cho mà tiếp xúc với trục Oy.BT15 : Cho họ đường tròn có phương trình:Tim để tiếp xúc vớiBT16 : Cho họ đường tròn có phương trình:Tìm để tiếp xúc với đường trònBT17 : Cho đường tròn có phương trình: .Viết phương trình tiếp tuyến củađường tròn đi qua .BT18 : Tìm các giá trị của a để hệ sau có đúng hai nghiệm
BT 19 : Cho đường tròn (T) có phương trình :a. Xác định tâm và bán kính của (T).b. Viết phương trình tiếp tuyến của (T), biết tiếp tuyến này vuông góc với đường thẳng (d) có phương trình12x – 5y + 2 = 0.BT 20 : Trong mặt phẳng Oxy cho đường tròn (C) : và đường thẳng (D) có phươngtrình :Tìm tọa độ điểm T trên (D) sao cho qua T kẻ được hai đường thẳng tiếp xúc với (C) tại hai điểm A , B vàBT 21 : Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn : và điểm.Gọi và là các tiếp điểm của các tiếp tuyến kẻ từ đến . Viết phương trình đường thẳng .BT 22: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) : và đườngthẳng d: . Tìm tọa độ điểm M nằm trên d sao cho đường tròn tâm M, có bán kính gấp đôi bánkính đường tròn (C), tiếp xúc ngoài với đường tròn (C)BT23: Trong mặt phẳng với hệ tọa độ 0xy cho hai điểm A (2; 0) và B (6; 4). Viết phương trình đường tròn(C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến điểm B bằng 5.BT24: Cho hai đường tròn :1. Xác định các giao điểm của và .2. Viết phương trình đường tròn đi qua 2 giao điểm đó và điểm A(0; 1)BT25 : Cho hai đường tròn :1. Xác định các giao điểm của và .2. Viết phương trình đường tròn đi qua 2 giao điểm đó và điểm A(0; 1)BT 26: Trong mặt phẳng với hệ tọa độ Đềcác vuông góc Oxy cho đường tròn (C) :và đường thẳng d : .Viết phương trình đường tròn (C’) đối xứng với đường tròn (C) qua đường thẳng d. Tìm tọa độ các giaođiểm của (C) và (C’) .