Download.vn Học tập Lớp 10
Bạn đang đọc: Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1
Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1 Lý thuyết và bài tập Hình học chương 1: Véctơ – tọa độ
Giới thiệu Tải về Bình luận
- 28
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đem đến cho các bạn học sinh có thêm nhiều tài liệu hoc tập môn Toán lớp 10, Download.vn xin giới thiệu đến các bạn tài liệu Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1 được chúng tôi tổng hợp và đăng tải ngay sau đây.
Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1 là tài liệu vô cùng hữu ích, gồm 72 trang, tóm tắt toàn bộ kiến thức lý thuyết chương véctơ – tọa độ và bài tập có đáp án chi tiết kèm theo sẽ giúp các bạn học sinh học tập hiệu quả bài tập Hình học lớp 10 chương 1. Chúc các em học tập và đạt được kết quả cao trong các kì thi sắp tới.
Tổng hợp lý thuyết và bài tập Hình học lớp 10 chương 1
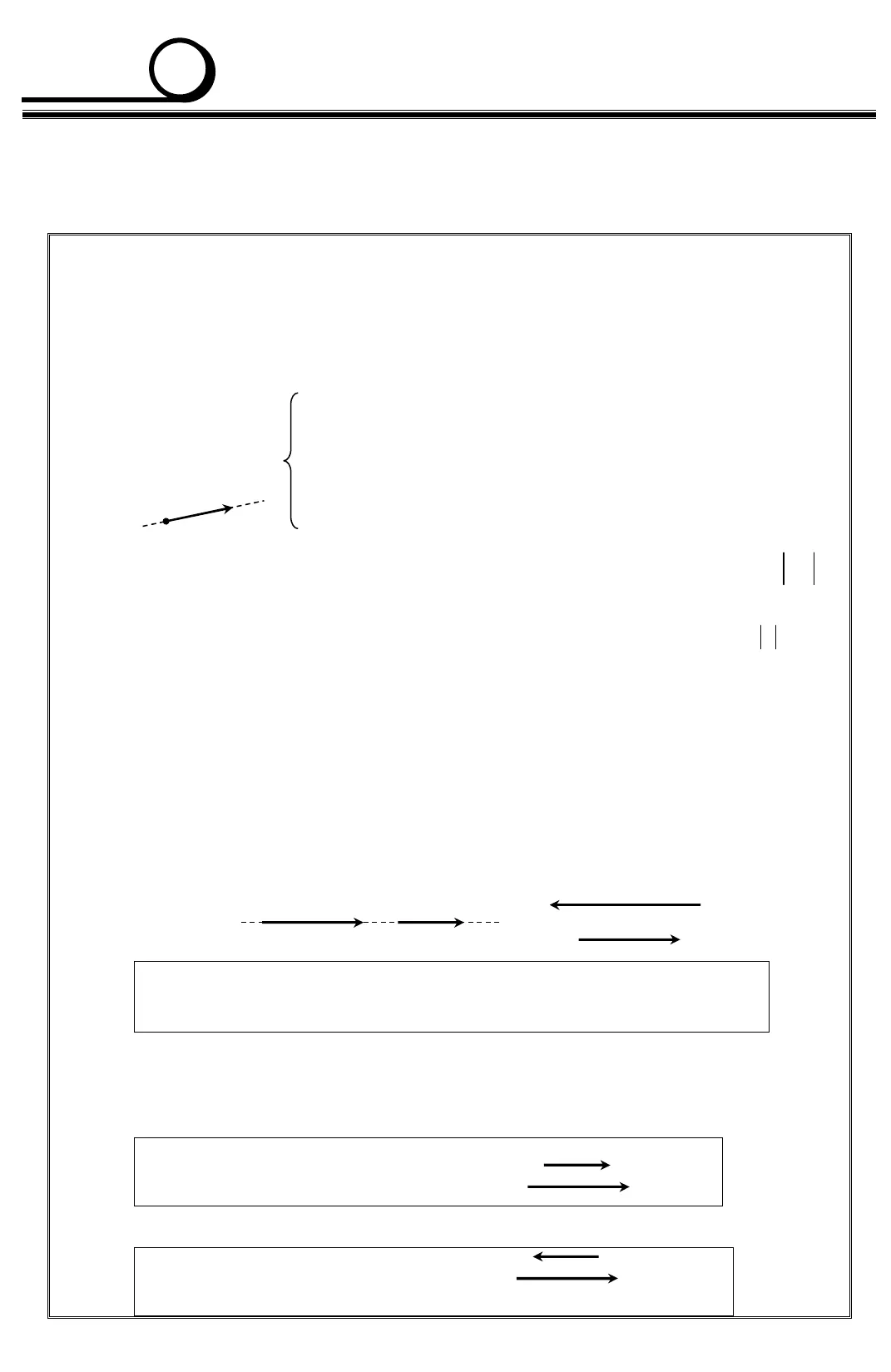Gv:TrầnQuốcNghĩa(Sưutầnvàbiêntập) 1 File word liên hệ: toanhocbactrungnam@gmail.com MS: HH10-C1 Ll20202020v,.VÉCTƠ – TỌA ĐỘBàiBài BàiBài 1111. VÉCT. VÉCT. VÉCT. VÉCTƠƠƠƠA – TÓM TẮT LÝ THUYẾT1. Kháiniệmmởđầu: Véctơ là một đoạn thẳng: • Một đầu được xác định là gốc, còn đầu kia là ngọn. • Hướng từ gốc đến ngọn gọi là hướng của véctơ. • Độ dài của véctơ là độ dài đoạn thẳng xác định bởi điểm đầu và điểm cuối của véctơ. Ví dụ: VéctơAB:• Điểm gốc: A • Điểm ngọn: B • Phương (giá): đường thẳng AB • Hướng: từ A đến B • Độ dài (môđun: độ dài đoạn AB Véctơ có gốc A, ngọn B được kí hiệu là và độ dài của véctơ ABđược kí hiệu là ABlàkhoảng cách giữa điểm đầu và điểm cuối của véctơ. Ngoài ra, véctơ còn được kí hiệu bởimột chữ cái in thường phía trên có mũi tên như, , , a b v uđộ dài của akí hiệu:a. Véctơ “không”, kí hiệu 0là véctơ có: • Điểm gốc và điểm ngọn trùng nhau. • Độ dài bằng 0. • Hướng bất kỳ Hai véctơ cùng phương khi chúng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song. Hai cặp véctơ (AB,CD) và (MN,PQ) được gọi là cùng phương. ABcùng phươngCD//⇔, , ,AB CDA B C D thaúng haøng Hướng của hai véctơ: Hai véctơ cùng phương có thể cùng hướng hoặc ngược hướng. Ta chỉ xét hướng của hai véctơ khi chúng cùng phương. • Hai véctơ ABvàCDgọi là cùng hướng:AB↑↑CD//,⇔AB CDHai tia AB CD cuøng höôùng• Hai véctơ ABvàCDgọi là ngược hướng:AB↑↓CD//,⇔AB CDHai tia AB CD ngöôïc höôùngABABCDMNQPABCDABDC2Chủđề
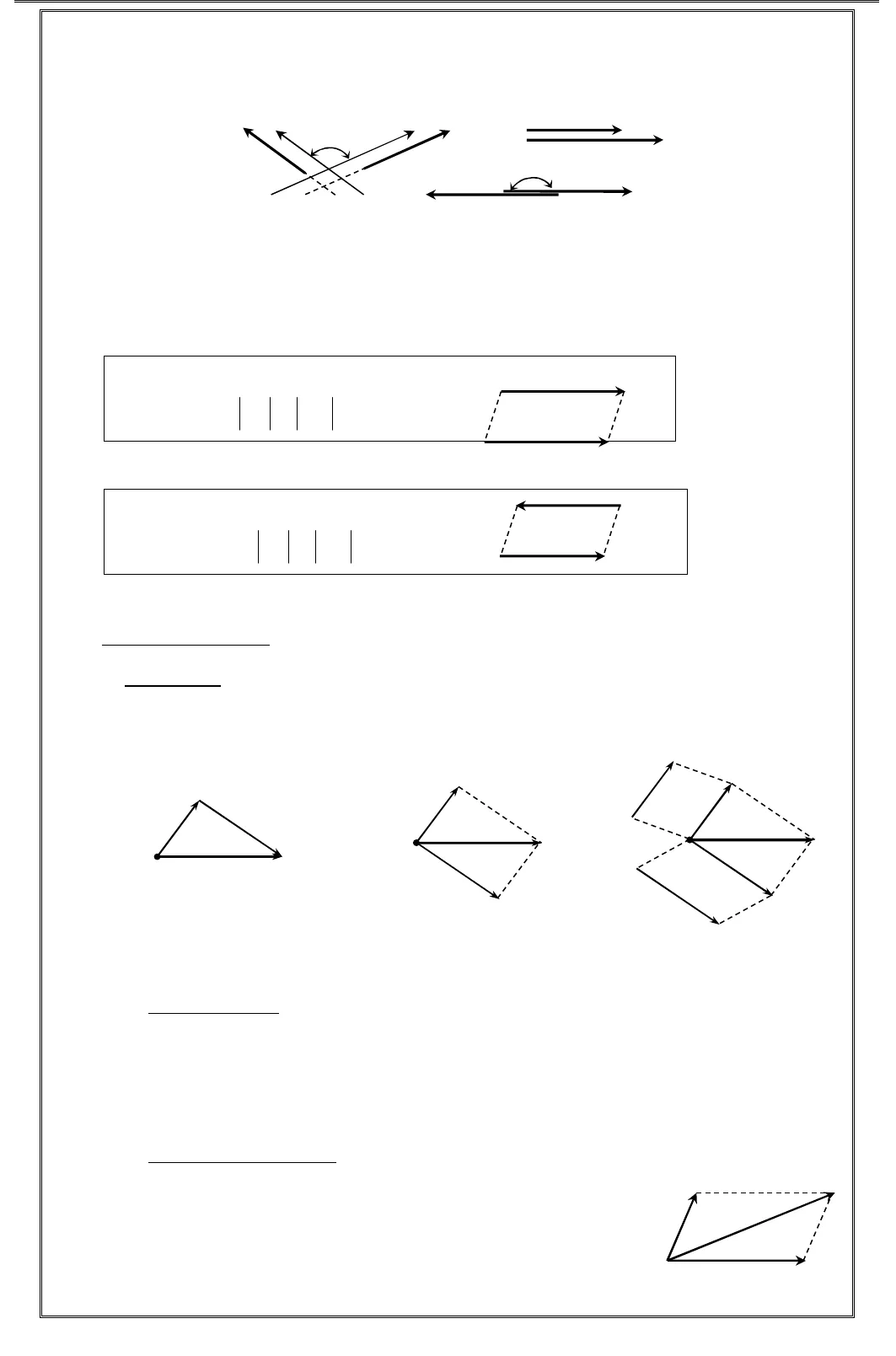TÀI LITÀI LITÀI LITÀI LIỆỆỆỆU HU HU HU HỌỌỌỌC TC TC TC TẬẬẬẬP TOÁN 10P TOÁN 10 P TOÁN 10P TOÁN 10 ––––HÌNH HHÌNH HHÌNH HHÌNH HỌỌỌỌCCCC –––– VÉCTVÉCTVÉCTVÉCTƠƠ ƠƠ –––– TTTTỌỌỌỌA ĐA ĐA ĐA ĐỘỘỘỘ 2222File word liên hệ: toanhocbactrungnam@gmail.com MS: HH10-C1 Góc của hai véctơ ABvàCDlà góc tạo bởi hai tia Ox, Oy lần lượt cùng hướng với haitia AB và CD. Nghĩa là:(),= xOy AB CD.• Khi ABvàCDkhông cùng hướng thì0 180xOy° ≤ ≤ °• Khi ABvàCDcùng hướng thì0xOy= °• Khi ABvàCDngược hướng thì180xOy= ° Hai véctơ bằng nhau khi và chỉ khi chúng cùng hướng và có độ dài bằng nhau. AB=CD⇔= = AB vaø CD cuøng höôùngAB CD hay AB CD Hai véctơ đối nhau khi và chỉ khi chúng ngược hướng và có độ dài bằng nhau. AB= −CD⇔= = AB vaø CD ngöôïc höôùngAB CD hay AB CD2. Cácphéptoántrênvectơ:a)a)a)a) TTTTổng của hai véctơổng của hai véctơổng của hai véctơổng của hai véctơ::::• Định nghĩa phép cộng 2 véctơ avàblà véctơa b+, được xác định tùy theo vị trí của2 véctơ này. Có 3 trường hợp:①①①①a b+nối đuôi ②②②②a b+cùng điểm gốc ③③③③a b+là 2 véctơ bất kỳa b+được cộng theoa b+được cộng theoa b+được cộng theo quy tắc 3 điểm quy tắc hình bình hành 2 trường hợp trên Qui tắc ba điểm: (Qui tắc tam giác hay qui tắc Chasles)– Với ba điểm bất kỳ A, B, C ta có: = + AB AC CB.– Qui tắc 3 điểm còn được gọi là hệ thức Chasles dùng để cộng các véctơ liên tiếp, có thể mở rộng cho trường hợp nhiều véctơ như sau:1 1 2 2 3 3 4 1…−= + + + + n n nA A A A A A A A A A Qui tắc hình bình hành:Cho hình bình hành ABCD thì”= += + AC AB ADDB DA DCvà== AB DCAD BC– Qui tắc hình bình hành dùng để cộng các véctơ chung gốc. Lưu ý: phép cộng véctơ không phải là phép cộng độ dài các véctơ.a b+aba b+aba b+baxABCDOy0 xOy 180° ≤ ≤ °DCABxO y 180= °CDABxO y 0= °ABCDABDCABCD
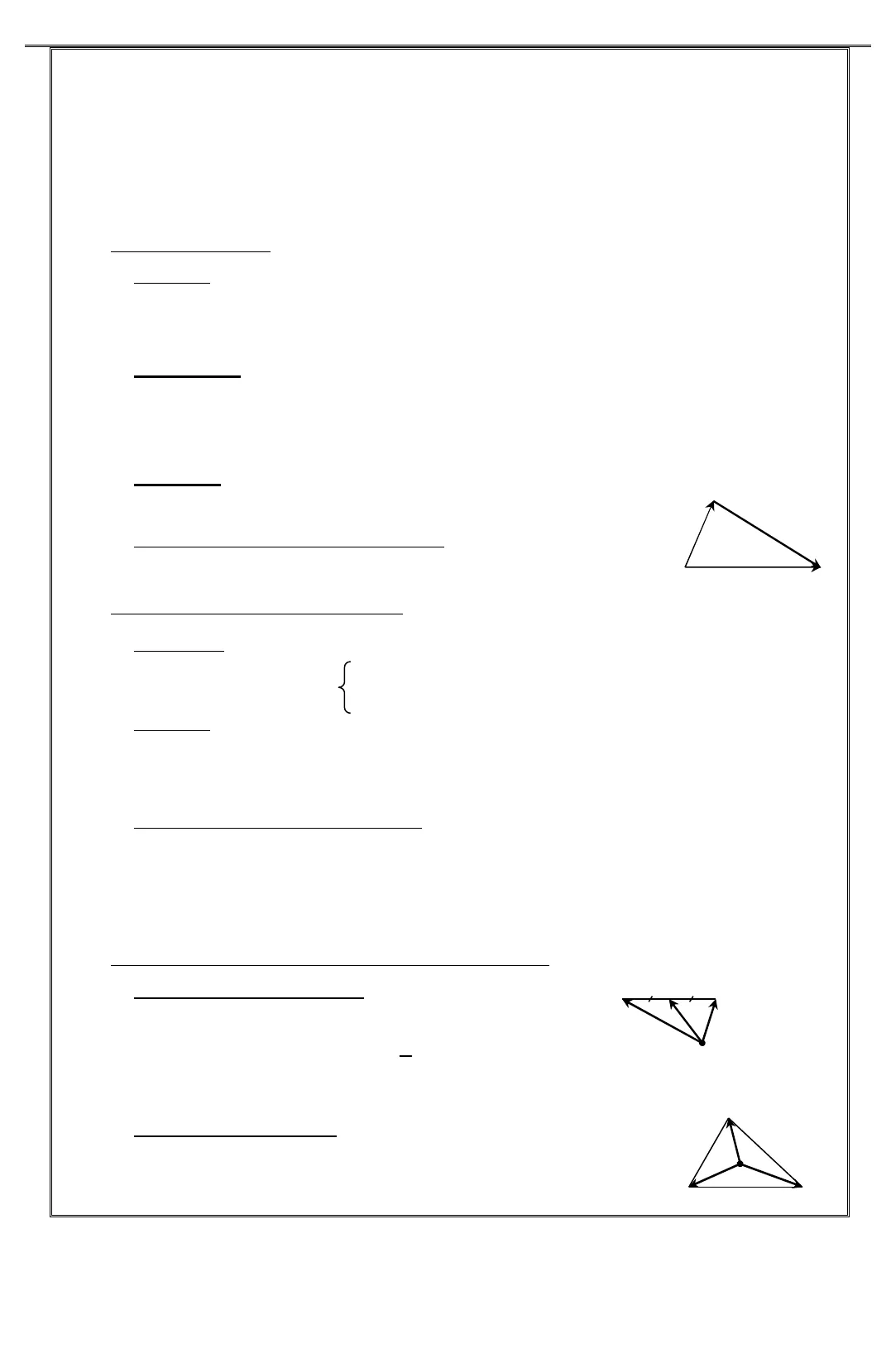Gv:TrầnQuốcNghĩa(Sưutầnvàbiêntập) 3 File word liên hệ: toanhocbactrungnam@gmail.com MS: HH10-C1 • Tính chất: Giao hoán: a b b a+ = + Kết hợp: ()()( )a b c a b c a c b+ + = + + = + + Cộng với véctơ đối: ()0a a+ − = . Cộng với véctơ không: 0 0a a a+ = + = .b)b)b)b) HiHiHiHiệu của hai véctơệu của hai véctơệu của hai véctơệu của hai véctơ:::: Véctơ đối: – Véctơ đối véctơ akí hiện là−a. – Tổng hai véctơ đối là 0:()0a a+ − = Định nghĩa: hiệu hai véctơ avà bcho2kết quảa b−hoặcb a−được xác định: (a b a− = + véctơ đối của())b a b= + − (b a b− = + véctơ đối của())a b a= + − Tính chất: ①①①①: 0a a a∀ − = ②②②②: 0a a a∀ − = ③③③③AB BA− = Qui tắc tam giác đối với hiện hai véctơ: Với ba điểm bất kỳ A,B,Cta có: = − AB CB CA. c)c)c)c) Tích cTích cTích cTích của một số đối với một véctơủa một số đối với một véctơủa một số đối với một véctơủa một số đối với một véctơ:::: Định nghĩa: Cho số thực k(0k≠) và một véctơa(a≠0) Tích k.alà một véctơ cùng hướng vớianếu0k> ngược hướng vớianếu0k Tính chất: (). .k a b k a k b+ = + (). . .k h a k a h a+ = + ()(). . . .k h a k h a= ()1 .a a− = − 1.= a a0. 0=a Điều kiện để hai véctơ cùng phương: – Điều kiện cần và đủ để hai véctơ ;a b(0≠b) cùng phương là tồn tại một sốkđể.=a k b.- Hệ quả: Điều kiện cần và đủ để 3 điểm A,B,Cthẳng hàng là= AB k ACd)d)d)d) Trung điTrung điTrung điTrung điểm của đoạn thẳng vểm của đoạn thẳng vểm của đoạn thẳng vểm của đoạn thẳng và trà trà trà trọng tâm tam giác:ọng tâm tam giác:ọng tâm tam giác:ọng tâm tam giác: Trung điểm của đoạn thẳng: – I là trung điểm của AB: ⇔0+ = IA IBhay12= = AI IB ABhay= − IA IB- Ilà trung điểm củaAB, vớiMbất kì, ta có:2+ = MA MB MI Trọng tâm của tam giác: G là trọng tâm của∆ABC⇔0+ + = GA GB GC- Với M bất kì: 3+ + = MA MB MC MGCBABAIMABGC